Correlation and Linear Regression

Correlations

Everything correlates with everything, which Paul Meehl calls the “crud factor” (aka Ambient Correlational Noise) (See Meehl, 1990ab and Lykken, 1968 cited by Meehl). Our goal is to determine how much and we will deal with 2 variables at a time, but we will soon explore the problems with 3 or more variables.

A few popular correlations between two variables:

• Pearson’s r (interval by interval) [for population = \(\rho\), for sample = \(r\)]
• Spearman’s rho (interval by ordinal) [for population = \(\rho_{s}\), for sample = \(r_s\)]
• Kendall’s tau [\(t\)] (interval by ordinal or ordinal by ordinal) like Spearman’s, but more accurate with small samples
• Point-by-serial (interval by dichotomous)
• Polychoric (ordinal vs ordinal) [used more in psychometrics or factor analysis of ordinal by ordinal]
• Tetrachroic (dichotomous vs dichotomous) [used more in psychometrics or factor analysis of dichotomous by dichotomous]

In general these assume bivariate normality, which means that the two variables are normally distributed when added together (and independently). The bivariate normal distribution is a three-dimensional normal curve.

Pearson’s Correlation

Most common type you will encounter and is a parametric method.

\[r_{xy}=\frac{\sum{(X-M_X)(Y-M_Y)}}{\sqrt{\sum(X-M_X)^2\sum(Y-M_Y)^2}}\] remember \(SS = (X-M)^2\), so thus,

\[r_{xy}=\frac{SP}{\sqrt{SS_XSS_Y}}\]

• Numerator = How much they vary together (covariance)
• Denominator = The product of how much they vary alone (variance)
• Values are bounded between -1 and 1

or more simply (see Cohen’s textbook for the derivation):

\[r_{xy}=\frac{\sum{xy}}{\sqrt{\sum{x^2}\sum{y^2}}}\]

Simulate Data

We will use the mvrnorm function (multivariate normal distribution) from the MASS package, but to do this we need to make a covariance matrix with a \(r = .60\) and set the mean values for each variable (which I will set to 5 for each)

#Set params
Means.XY<- c(5,5) #set the means of X and Y variables
r=.6 #Correlation value
CovMatrix.XY <- matrix(c(1,r,
                         r,1),2,2) # creates the covariate matrix 

# Build the correlated variables using mvrnorm. 
# Note: empirical=TRUE means make the correlation EXACTLY r. 
# empirical=FALSE, the correlation value would be normally distributed around r
library(MASS) #create data
CorrData<-mvrnorm(n=100, mu=Means.XY,Sigma=CovMatrix.XY, empirical=TRUE)

#Convert them to a "Data.Frame", which is like SPSS data window
CorrData<-as.data.frame(CorrData)
#lets add our labels to the vectors we created
colnames(CorrData) <- c("Happiness","IceCream")

Plot the data

#make the scatter plot
library(ggpubr) #graph data
ggscatter(CorrData, x = "IceCream", y = "Happiness",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   )

Run Pearson’s r

The cor.test function runs Pearson’s correlation. Note: You will notice that I have attached the data frame to each variable.

Corr.Result.1<-cor.test(CorrData$Happiness, CorrData$IceCream, 
         method = c("pearson"))
Corr.Result.1

## 
##  Pearson's product-moment correlation
## 
## data:  CorrData$Happiness and CorrData$IceCream
## t = 7.4246, df = 98, p-value = 4.193e-11
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.4574985 0.7124547
## sample estimates:
## cor 
## 0.6

You can also call the function via a formula command.

Corr.Result.1<-cor.test(~Happiness + IceCream, data= CorrData,  
         method = c("pearson"))

Pvalue on Pearson’s Correlation

The classical pvalue on Pearson’s correlation is adapted from the t-distribution. We will come back to later when we cover linear regression.

Report them in APA format

The cor_apa function in the APA package will report it in APA format for you. Note: r(df) = pearson r, pvalue. DF here is N-2, as we have two variables we are comparing. There are lots of options regarding how to output the format.

library(apa)
cor_apa(Corr.Result.1,format ="rmarkdown")

r(98) = .60, p < .001

Pearson’s correlation is scale-independent!

No matter the mean differences or range of scores, the Pearson’s r will give the same results. We can also z-score the data and get the same result. However, if they are scaled non-linearly (sqrt, ^2, log,…) the correlation will change.

Lets add (change the mean)

CorrData$Happiness.big<-CorrData$Happiness+1000

ggscatter(CorrData, x = "IceCream", y = "Happiness.big",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   )

cor_apa(cor.test(CorrData$Happiness.big, CorrData$IceCream, 
         method = c("pearson")),format ="text")

## r(98) = .60, p < .001

Z-scored

Remember that, \(Z = \frac{X-M}{S}\)

CorrData$Happiness.z<-scale(CorrData$Happiness)
CorrData$IceCream.z<-scale(CorrData$IceCream)

ggscatter(CorrData, x = "IceCream.z", y = "Happiness.z",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   )

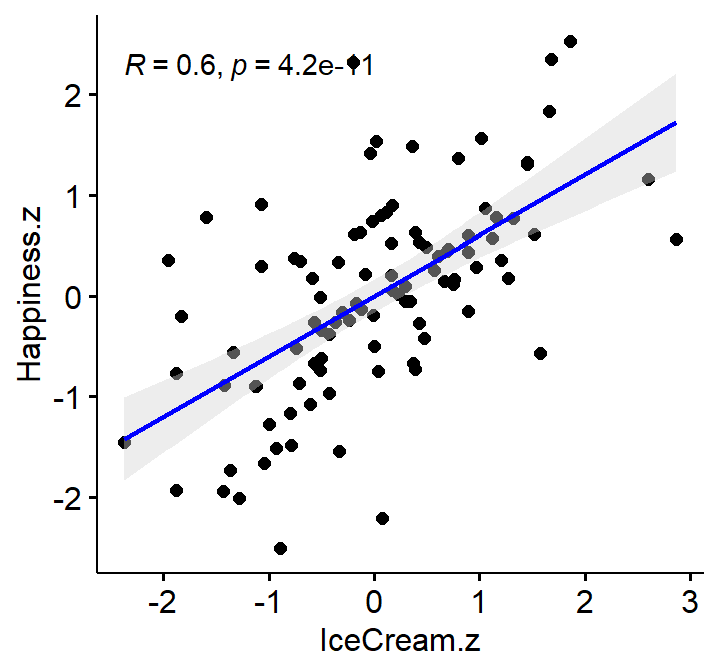
cor_apa(cor.test(CorrData$Happiness.z, CorrData$IceCream.z, 
         method = c("pearson")),format ="text")

## r(98) = .60, p < .001

What happens if I LINEARLY scale them differently?

ggscatter(CorrData, x = "IceCream.z", y = "Happiness.big",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   )

cor_apa(cor.test(CorrData$Happiness.big, CorrData$IceCream.z, 
         method = c("pearson")),format ="text")

## r(98) = .60, p < .001

What happens if I NON-LINEARLY scale them differently?

CorrData$Happiness<-CorrData$Happiness # orginal
CorrData$IceCream.sq4<-(CorrData$IceCream)^4 #Non-linear

ggscatter(CorrData, x = "IceCream.sq4", y = "Happiness",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   )

cor_apa(cor.test(CorrData$Happiness, CorrData$IceCream.sq4, 
         method = c("pearson")),format ="text")

## r(98) = .54, p < .001

Pearson’s: Let visualize our result

The overlap between the two variables is defined by \(r^2\)

 # lets us plot our results (like the book)
library(VennDiagram)
# calculate r-squared
overlap=r^2 

Simple.Corr.Venn<-draw.pairwise.venn(1, 1, overlap, c("Happiness", "IceCream"))
grid.draw(Simple.Corr.Venn)

This means that 36% of the variance of happiness overlaps with ice cream consumption. Can we conclude ice cream causes happiness? No, because we did not design a study with a control group. We can not infer causation. It seems to make sense to say “eating ice cream causes me to be happy”, but the opposite could be true as well “happiness causes me to eat ice cream”. How do I know which causes which? We cannot without an experiment.

Non-Parametric Correlations

Spearmen and Kendall correlation can be used for ordinal data, but should be used if you have a “bend” (non-linear relationship) between variables.

Spearmen’s Correlation

Spearman is a Pearson Correlation on rank-ordered data. Let’s rank order our random correlated data. You must rank each variable independently first (where ties are averaged).

CorrData$Happiness.rank<-rank(CorrData$Happiness)
CorrData$IceCream.rank<-rank(CorrData$IceCream)

ggscatter(CorrData, x = "IceCream.rank", y = "Happiness.rank",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

cor_apa(cor.test(CorrData$IceCream.rank, CorrData$Happiness.rank, method = c("pearson")))

## r(98) = .61, p < .001

You should use the built-in Spearman correlation (cor.test, but pass method = c(“spearman”)) because the pvalues are calculated differently and ranks the raw data automatically.

# APA format (note the S should be subscript)
cor_apa(cor.test(CorrData$IceCream, CorrData$Happiness, 
         method = c("spearman")),format ="text")

## r_s = .61, p < .001

Pearson vs Spearman’s Correlation for slight nonlinearity

Let’s say you get some data and clearly there is a slight nonlinearity in the relationship between the two variables. Pearson is designed for linear relationships and we can see the problem in our fitted line below.

CorrNL<-data.frame(Var1=c(0,1,3,5,7,9,12,15,18),
                   Var2=c(0,3,12,18,19,20,21,22,23))

ggscatter(CorrNL, x = "Var1", y = "Var2",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

## r(7) = .86, p = .003

If we switch to a Spearman correlation the data are converted to ranks and the “bump” is now gone and our correlation gets stronger.

CorrNL$Var1.rank<-rank(CorrNL$Var1)
CorrNL$Var2.rank<-rank(CorrNL$Var2)

ggscatter(CorrNL, x = "Var1.rank", y = "Var2.rank",
   add = "reg.line",  # Add regressin line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

## r_s = 1.00, p < .001

Kendall’s Tau

Kendall tau will always be more conservative than spearman correlation and is generally more robust (cor.test, but pass method = c(“kendall”)). It is safer to use but less widely known.

# APA format (note the S should be subscript)
cor_apa(cor.test(CorrNL$Var1, CorrNL$Var2, 
         method = c("kendall"), exact =TRUE),format ="text")

## r_tau = 1.00, p < .001

Ties

One of the problems with Spearman’s and Kendall’s correlation is that you need to account for ties in the data (two or more people have the same score; a not uncommon problem in ordinal data). R and SPSS automatically account for ties and using the exact pvalue parameter will account for these issues. Thus while I rank ordered the data manually to show you how it compared to Pearson correlation let the functions in R do this work for you.

Point-by-Serial Correlation

This correlation is for interval by dichotomous. See the simulation below. Note: We use to calculate the these by hand in the old days using t-test and converting the \(d\) into \(r\) or by just using the Pearson formula (but these approaches overestimate the correlations).

set.seed(42)
Ratings<-c(rnorm(25,mean=5,sd = .5),rnorm(25,mean=2,sd = .5))
Flavors<-c(rep(0,25),c(rep(1,25)))
FlavorNames<-c(rep("Cookie Dough",25),c(rep("Rum-Raisin",25)))

#Build data frame
Ice.Cream.Data<-data.frame(
  Ratings = Ratings,
  Flavors = Flavors,
  Names = FlavorNames)
#head(Ice.Cream.Data)

ggscatter(Ice.Cream.Data, x = "Flavors", y = "Ratings",
   add = "reg.line",  # Add regression line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

Calculation of Point-by Serial

using the polycor package, we can run polyserial function using maximum-likelihood estimation (generally more accurate when the underlying distribution is normal). I will explain MLE function later in the semester.

library(polycor) #Advanced Correlations
PbySerial<-with(Ice.Cream.Data, 
     polyserial(Flavors,Ratings, ML=TRUE))
PbySerial

## [1] -0.8091302

Polychoric

Most people will default to using a Pearson/Spearman correlation for ordinal vs ordinal data, but actually that is an inaccurate analysis. Pearson’s correlation assumes the variances are unbounded, but in ordinal data the variances that is not the case. Polychoric correlations are particularly helpful for when you want an accurate factor analysis of ordinal scales. However, this is only commonly done by people in educational psychology. These correlations require more data for the models to converge than Pearson correlations matrices. We will simulate 1-5 Likert scale with the simstudy package.

library(simstudy)
baseprobs <- matrix(c(0.10, 0.20, 0.10, 0.40,0.20,
                      0.20, 0.10, 0.30, 0.10,0.30),
                    nrow = 2, byrow = TRUE)

# generate the data
set.seed(1234)                  
Ns=genData(50)
SimOrdData <- genCorOrdCat(Ns, adjVar = NULL, baseprobs = baseprobs, 
                   prefix = "Variable", rho = 0.5, corstr = "cs")

SimOrdData<-as.data.frame(SimOrdData)
ggscatter(SimOrdData, x = "Variable1", y = "Variable2",
   add = "reg.line",  # Add regression line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

library(polycor) #Advanced Correlations
PolyCorrR<-with(SimOrdData, 
     polychor(Variable1,Variable2, ML=TRUE))

We get a polychroic correlation of 0.59. Compare that to do the Pearson, r(48) = .53, p < .001, and Spearman, \(r_s\) = .58, p < .001, correlations.

Tetrachroic

Like Polychoric, but used for dichotomous vs dichotomous. We will simulate 2 items on a test (that are right [true] or wrong false]) with the simstudy package. These assume the bivariate normality So here we are predicting how well one item on a test predicts the others. Note

library(simstudy)
baseprobs1 <- matrix(c(0.35, 0.65,
                      0.50, 0.50),
                    nrow = 2, byrow = TRUE)

# generate the data
set.seed(1234)                  
SimOrdData2 <- genCorOrdCat(Ns, adjVar = NULL, baseprobs = baseprobs1, 
                   prefix = "Variable", rho = 0.6, corstr = "cs")

SimOrdData2<-as.data.frame(SimOrdData2)
ggscatter(SimOrdData2, x = "Variable1", y = "Variable2",
   add = "reg.line",  # Add regression line
   add.params = list(color = "blue", fill = "lightgray"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   )

with(SimOrdData2, 
     polychor(Variable1,Variable2))

## [1] 0.6575174

Correlation Matrices

When we have multiple variables we can compare them all to each other at once. First we will simulate a 4 variables and all their bivariate correlations using the mvrnorm function again.

#Set params
Means.XY<- c(5,5,5,5) #set the means of X and Y variables
r12=.6;r13=.1;r14=.5;r23=.1;r24=.8;r34=0; #Correlation values
CovMatrix.XY <- matrix(c(1,r12,r13,r14,
                         r12,1,r23,r24,
                         r13,r23,1,r34,
                         r14,r24,r34,1),4,4) # creates the covariate matrix 

# Build the correlated variables using mvrnorm. 
# Note: empirical=TRUE means make the correlation EXACTLY r. 
# empirical=FALSE, the correlation value would be normally distributed around r
library(MASS) #create data
CorrData2<-mvrnorm(n=100, mu=Means.XY,Sigma=CovMatrix.XY, empirical=TRUE)
#Convert them to a "Data.Frame", which is like SPSS data window
CorrData2<-as.data.frame(CorrData2)
#lets add our labels to the vectors we created
colnames(CorrData2) <- c("Happiness","IceCream", "Sprinkles","Oreos")

We can use the GGally package to plot Pearson correlations quickly in an easy to visualize format once the data are in a data frame.

library(GGally)
CorrPlot <- ggpairs(CorrData2,  
              lower = list(continuous = "smooth"))
CorrPlot

Regression

• Correlation and regression are similar
• Correlation determines the standardized relationship between X and Y
• Linear regression = 1 DV and 1 IV, where the relationship is a straight line
• Linear regression determines how X predicts Y
• Multiple (linear) regression = 1 DV and 2+ IV (also straight lines)
• Multiple regression determines how X,z, and etc, predict Y [next week]

Basic Regression Equation

• Linear Regression equation you learned when younger was probably \(y = MX + b\)
• \(y\) = predict value
• \(M\) = slope
• \(X\) = Variable used to predict Y
• \(b\) = intercept

Modern Regression Equation

• \(Y=B_{YX}X + B_0 + e\)
• \(Y\) = predict value
• \(B_{YX}\) = slope
• \(B_{0}\) = intercept
• \(e\) = error term (observed - predicted). Also called the residual.

Ice Cream example

• Specify the model with the lm function.
• We are going to predict happiness scores from ice cream!

Happy.Model.1<-lm(Happiness~IceCream,data = CorrData)
summary(Happy.Model.1)

## 
## Call:
## lm(formula = Happiness ~ IceCream, data = CorrData)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.24894 -0.43244 -0.05275  0.44217  2.43434 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.00000    0.41198   4.855 4.56e-06 ***
## IceCream     0.60000    0.08081   7.425 4.19e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8041 on 98 degrees of freedom
## Multiple R-squared:   0.36,  Adjusted R-squared:  0.3535 
## F-statistic: 55.13 on 1 and 98 DF,  p-value: 4.193e-11

Intercept

• 2 is where the line hit the y-intercept (when happiness = 0).

Slope

• 0.6 is the rise over run
• for each 0.6 change in ice cream value, there is a corresponding change in happiness!
• so we can predict happiness from ice cream score:

(0.6 * 5 spoons of ice cream + baseline happiness intercept: 2) = 5

• This is your predicted happiness score if you had 5 spoons of ice cream

Error for this prediction?

R will do all the prediction for us for each value of ice cream residuals = observed - predicted

• Red dots = observed above predictor line
• Blue dots = observed below predictor line
• the stronger the color, the more an impact that point has in pulling the line in its direction
• Hollow dots = predicted
• The gray lines are the distance between observed and predicted values!

What should the mean of the residuals equal?

CorrData$predicted <- predict(Happy.Model.1)   # Save the predicted values with our real data
CorrData$residuals <- residuals(Happy.Model.1) # Save the residual values

library(ggplot2) 
ggplot(data = CorrData, aes(x = IceCream, y = Happiness)) +
  geom_smooth(method = "lm", se = FALSE, color = "lightgrey") +  # Plot regression slope
  geom_point(aes(color = residuals)) +  # Color mapped here
  scale_color_gradient2(low = "blue", mid = "white", high = "red") +  # Colors to use here
  guides(color = FALSE) +
  geom_segment(aes(xend = IceCream, yend = predicted), alpha = .2) +  # alpha to fade lines
  geom_point(aes(y = predicted), shape = 1) +
  theme_bw()  # Add theme for cleaner look

Ordinary least squares (OLS)

• Linear regression finds the best fit line by trying to minimize the sum of the squares of the differences between the observed responses those predicted by the line.
• OLS computationally simple to get the slope value, but is inaccurate

\[B_{YX}=\frac{\sum{XY}-\frac{1}{n}\sum{X}\sum{Y}}{\sum{x^2}-\frac{1}{n}\sum{x}^2} = \frac{Cov_{XY}}{var_x}\]

• Modern methods use an alternative (ML, REML) we will examine later when we get to GLM

SE on the terms in the models (how good is the fit?)

• Residual Standard error = \(\sqrt\frac{\sum{e^2}}{n-2}\)
• in R language:

n=length(CorrData$residuals)

RSE = sqrt(sum(CorrData$residuals^2) / (n-2))
RSE

## [1] 0.8040713

• So, our error on the prediction is 0.8040713 happiness points based on our model.

SE on the Intercept

• Intercept Standard error = \(RSE\sqrt {\frac{1}{n}+\frac{M_x^2}{(n-1)var_x}}\)
• in R language:

ISE = RSE*(sqrt( 1 / n + mean(CorrData$IceCream)^2 / (n - 1)*var(CorrData$IceCream)))
ISE

## [1] 0.4119838

SE on the Slope

• Slope Standard error = \(\frac{sd_y}{sd_x}\sqrt{\frac{1 - r_{YX}^2}{n-2}}\)
• in R language:

#lets extract the r2 from the model
r2.model<-summary(Happy.Model.1)$r.squared

SSE = sd(CorrData$Happiness)/sd(CorrData$IceCream) * sqrt((1- r2.model)/ (n - 2))
SSE

## [1] 0.0808122

t-tests on slope and intercept and \(r^2\) value

• Values are tested against 0, so its all one sample t-tests
• slope: \(t = \frac{B_{YX} - H_0}{SE_{B_{YX}}}\)
• intercept: \(t = \frac{B_{0} - H_0}{SE_{B_{0}}}\)

\(r^2\) is a little different as its a correlation value

• correlations are not normally distributed
• Fisher created a conversion for r to make it a z (called Fishers’ \(r\) to \(Z\))
• \(r^2\): \(t = \frac{r_{XY}\sqrt{n-2}-H_0}{\sqrt{1-r_{XY}^2}}\) , where \(df = n - 2\)
• its often given for as an F value, remember \(t^2 = F\)

#intercept
t.I= Happy.Model.1$coefficients[1]/ISE
t.I

## (Intercept) 
##     4.85456

#Slope
t.S= Happy.Model.1$coefficients[2]/SSE
t.S

## IceCream 
## 7.424621

# For r-squared
t.r2xy = r2.model^.5*sqrt(n-2)/sqrt(1-r2.model)
F.r2xy = t.r2xy^2
F.r2xy

## [1] 55.125

Note: We are testing null hypothesis value for slope, i.e., null = 0. But it’s a terrible guess. Everything correlates with everything, so it’s important to keep this in mind moving forward. So that would be the NILL hypothesis. NILL can be tested better with bootstrapping.

Regression in ANOVA format

• You can also report the results of all the predictors (if you have multiple) in ANOVA style format (F-test we calculated above on \(r^2\))
• This is useful in multiple regression as it tell your if your overall set of predictors is significant

anova(Happy.Model.1)

## Analysis of Variance Table
## 
## Response: Happiness
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## IceCream   1  35.64  35.640  55.125 4.193e-11 ***
## Residuals 98  63.36   0.647                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Power and Regression

For regression, we will need to convert our \(r^2\) into cohen’s \(f^2\)

\[f^2 = \frac{r^2}{1-r^2}\]

Power Calculation

We will use the pwr package.

library(pwr) #power analysis
#power for GLM
# u  = degrees of freedom for numerator
# v = degrees of freedom for denominator
# f2 = effect size
# sig.level= (Type I error probability)
# power = (1 minus Type II error probability)
f2.icecream <- r^2 / (1-r^2)

pwr.f2.test(u = 1, v = n-2, f2 = f2.icecream, sig.level = 0.05, power = NULL)

## 
##      Multiple regression power calculation 
## 
##               u = 1
##               v = 98
##              f2 = 0.5625
##       sig.level = 0.05
##           power = 1

So we had a power of basically 1 given this sample size and our true effect size of 0.6

A Priori Power Analysis

• What sample size do I need given a specific \(f^2\)
• Note: Gpower might use \(f\), not \(f^2\)

#power for GLM
# u  = degrees of freedom for numerator
# v = degrees of freedom for denominator
# f2 = effect size
# sig.level= (Type I error probability)
# power = (1 minus Type II error probability)

pwr.f2.test(u = 1, v = NULL, f2 = f2.icecream, sig.level = 0.05, power = .80)

## 
##      Multiple regression power calculation 
## 
##               u = 1
##               v = 14.12059
##              f2 = 0.5625
##       sig.level = 0.05
##           power = 0.8

Final Notes

• Testing between correlations using old fashion Fisher’s test is old fashion (Cohen et al., p. 49). The modern approach is the bootstrap, as the old method is underpowered.
• Your book is a little out of date: CIs are better but bootstrapped CIs are becoming more standard. We will cover that later in the semester.

References

Lykken, D. T. (1968). Statistical significance in psychological research. Psychological bulletin, 70(3p1), 151.

Meehl, P. E. (1990a). Appraising and amending theories: The strategy of Lakatosian defense and two principles that warrant it. Psychological inquiry, 1(2), 108-141.

Meehl, P. E. (1990b). Why summaries of research on psychological theories are often uninterpretable. Psychological reports, 66(1), 195-244.