Pearson’s Chi-Square and Other Useful Non-Parametrics

Parametric vs. Non-Parametric

• Parametric tests: the tests we have studied so far (z, t, F) have been used to describe a populations distribution (parameters).
  • Require interval or ratio data
• Non-Parametric tests: describe relationships about that exist in populations but make relaxed (or different) assumptions about populations distributions.
  • These tests can compare qualitative data (e.g., chi-squared)
  • Non-parametric tests are more likely to commit type II errors
  • Typically are used with ordinal or nominal data, but can also be used with interval or ratio data when parametric assumptions are not met (e.g., when variance or distribution presents a problem).
    • These tests do not use the mean and standard deviation since they are often meaningless in ordinal data.
    • These tests rank scores to see how different groups compare to each other.

One-Way Pearson’s Chi-Squared [Goodness of Fit]

Have you been told: “Stay with your first answer on a multiple-choice test.” So is changing answers more likely to be harmful?

Best (1979) studied the responses of 261 students in an introductory psychology course. He recorded the number of right-to-wrong (27), wrong-to-right (195), and wrong-to-wrong (39) answer changes for each student. Note: We will ignore wrong-to-wrong as he did in his first analysis.

Frequency	Right-to-Wrong	Wrong-to-Right
Observed	27	195

Total of 222 observations

We will use the One-Way Chi-Squared [Goodness of fit]. It asks whether the relative frequencies observed in the categories of a sample frequency distribution are in agreement with the relative frequencies hypothesized to be true in the population.

Hypothesis for Goodness of fit

There are two versions:

• No preference: there will be no preference between different categories (e.g., do people prefer Coke or Pepsi)
• No difference from a known population: This type hypothesis compares two populations (or representative samples)

If people were making chance guesses from a population of people who don’t have any knowledge about material on the test (version 2 of the hypothesis):

• \(H_0: P_{right-to-wrong} = .5, P_{wrong-to-right} = .5\)
• \(H_1: H_0\) is False

Note: The probability you set can be whatever you want, but across all cells, they must add to 1. When you do not know what probability should be from a theoretical standpoint, you can simply do 1/Number of cells.

Find Expected Frequencies

If we expect by chance people would have gotten p = .50 on wrong-to-right and right to wrong, \(f_e = pn\)

\(E_{right-to-wrong}= .5*222=111\) \(E_{wrong-to-right}= .5*222=111\)

Frequency	Right-to-Wrong	Wrong-to-Right
Observed	27	195
Expected	111	111

Note: These tables are often shown in papers (sometimes as proportions).

Goodness of Fit Calculation by Hand

\[\chi^2 = \sum \frac{(f_o-f_e)^2}{f_e}\]

\(\chi^2 = \frac{(27-111)^2}{111}+\frac{(195-111)^2}{111} = 127.14\)

Note: Never enter proportions into the chi-square. You must work with frequencies.

Test Against Distribution

The chi-square distribution is a non-parametric distribution [not normal] (see handout). Like the F-test, it has no tails. The distribution changes as a function of the degrees of freedom [\(df\) is the number of cells - 1]

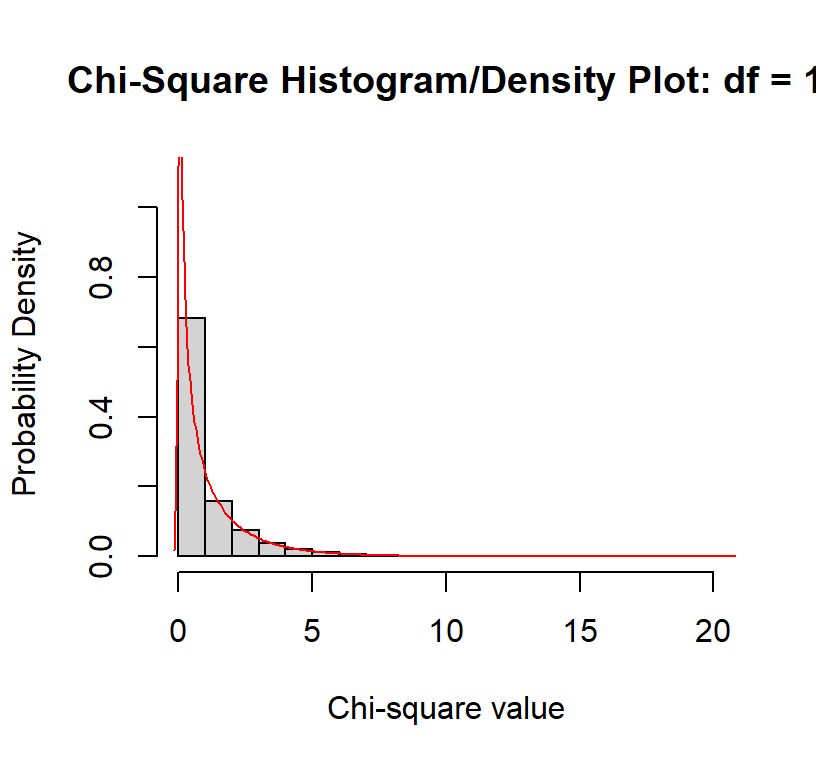
Just like the F-test we ask where is our chi-square value relative to this chance distribution given our \(df = 1\). We calculated 127.14, and that is in the tail. We can use R or a table to get the critical values for alpha =.05

Crit.MCQ=qchisq(.05, df=1, lower.tail = FALSE)

We get the crit = 3.8414588 < 124.14, so we reject the null.

Impact of higher DF

Just like in F-tests the shape of chance distribution changes as we have more df.

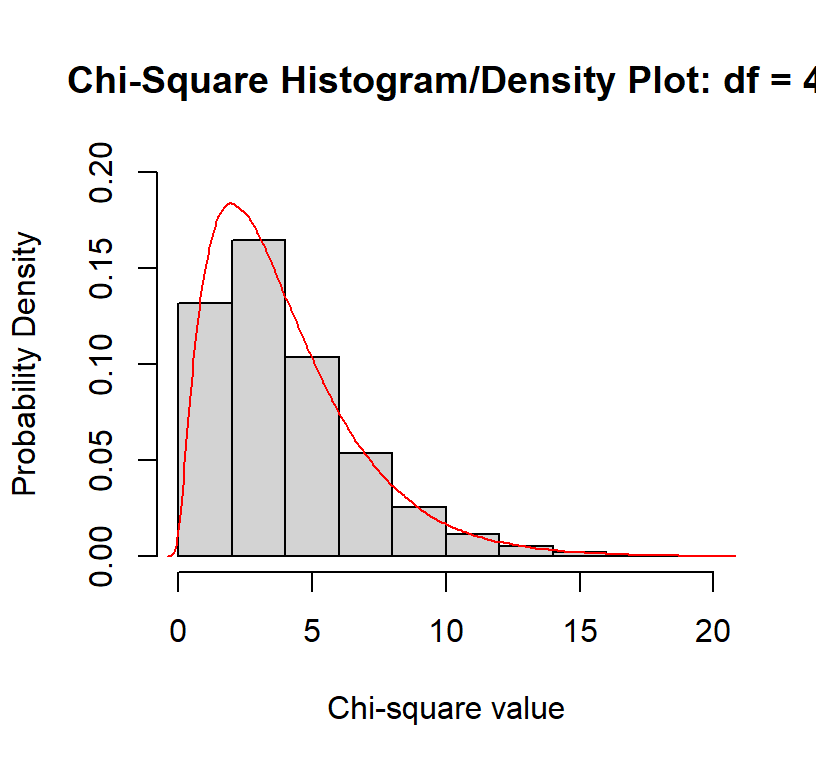
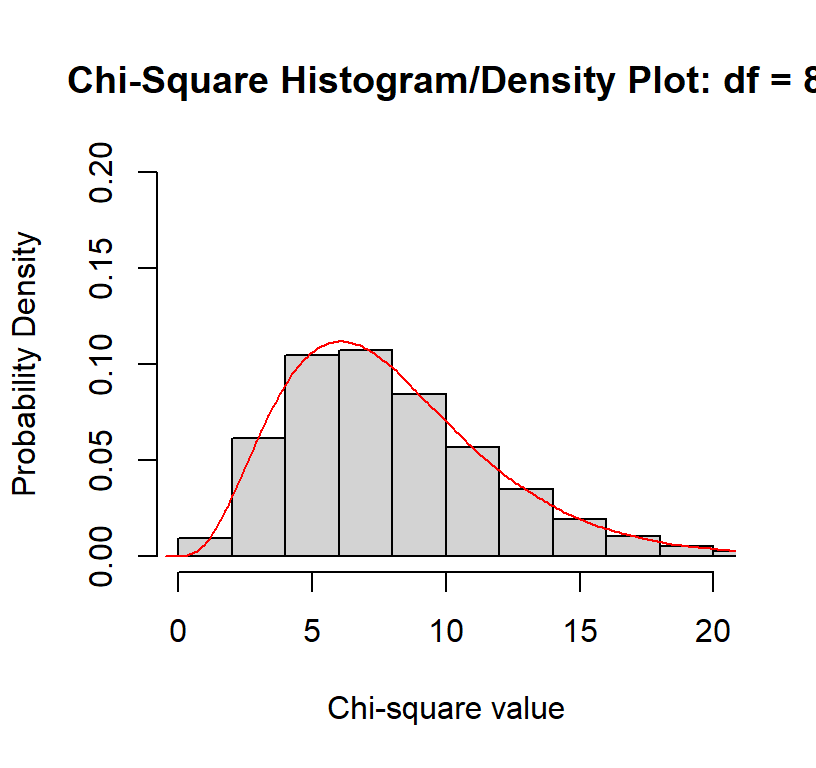
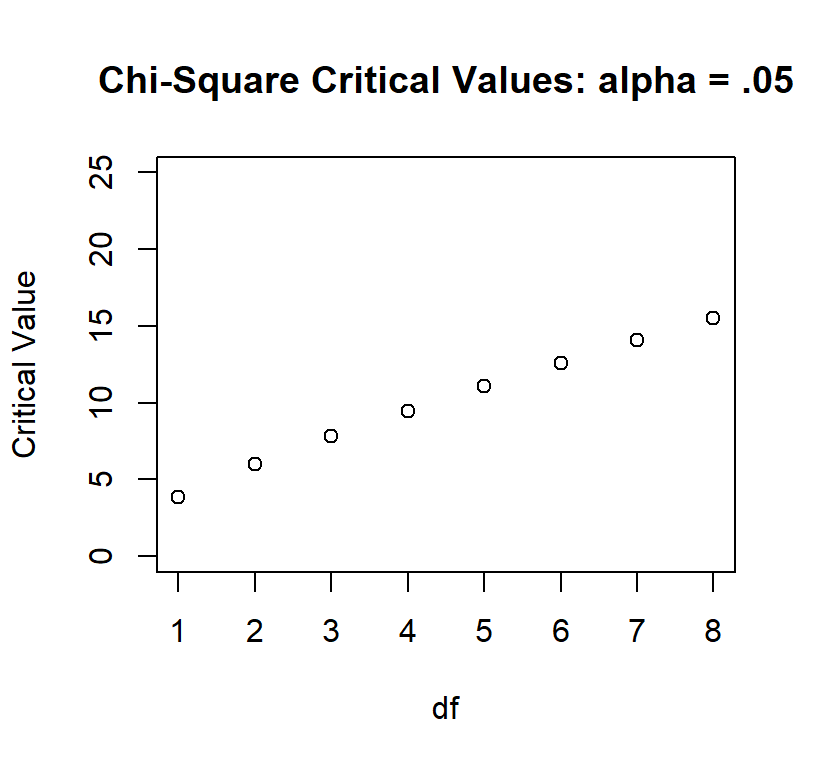
As you can see the distribution gets more spread out. So with larger DF our critical value increases

ChiCrit<-qchisq(.05, 1:8, lower.tail = FALSE)
plot(ChiCrit, main="Chi-Square Critical Values: alpha = .05",
  xlab="df", ylab="Critical Value", xlim=c(1,8), ylim=c(0,25))

Goodness of Fit Calculation by Code

Step 1: Build your Table

MCQ.Study <- as.table(rbind(c(27, 195)))
dimnames(MCQ.Study) <- list(Freq = c("Observed"),
                           Action = c("RtoW", "WtoR"))
MCQ.Study

##           Action
## Freq       RtoW WtoR
##   Observed   27  195

Step 2: Calculate Chi-squared

(MCQ.chi <- chisq.test(MCQ.Study, p=c(.5, .5)))

## 
##  Chi-squared test for given probabilities
## 
## data:  MCQ.Study
## X-squared = 127.14, df = 1, p-value < 2.2e-16

Step 2a: Calculate chi-square via Monte Carlo simulation

In the goodness-of-fit simulation is done by random sampling from the discrete distribution specified by p, each sample being the total number of observations (see ?chisq.test for more details on the simulation process)

(MCQ.chi <- chisq.test(MCQ.Study, p=c(.5, .5), simulate.p.value = TRUE, B = 10000))

## 
##  Chi-squared test for given probabilities with simulated p-value (based
##  on 10000 replicates)
## 
## data:  MCQ.Study
## X-squared = 127.14, df = NA, p-value = 9.999e-05

Step 3: Report in APA

\(\chi^2(df,N) = X.XX, p < |= .XXX\)

Since our result was p-value < 2.2e-16

\(\chi^2(1,N = 222) = 124.14, p < .0001\)

There is a difference how people change their items, and we can see from the frequencies that should change their answers if they are unsure.

Two-Way Pearson’s Chi-Squared [Test of Independence]

“Maybe we should only change our answers on easy items, but on hard items, we should trust ourselves.”

Best (1979) also examined the 1670 total number of responses across the 261 students and divided the items into easy/difficult in an introductory psychology course. He recorded the number of right-to-wrong, wrong-to-right, and wrong-to-wrong (39) answer changes for each student. Again we will ignore wrong-to-wrong (17% of the responses) for simplicity.

Frequency	Right to Wrong	Wrong to Right
Easy	97	411
Difficult	251	620

We need to do a Two-Way Chi-Square [Test of Independence]. It asks whether observed frequencies reflect the independence of two qualitative variables. Compares the actual observed frequencies of some phenomenon (in our sample) with the frequencies we would expect if there were no relationship at all between the two variables in the larger (sampled) population. We ask if the two variables are independent: knowledge of the value of one variable provides no information about the value of another variable.

Hypothesis for Test of Independence

The null hypothesis is that for each, the value obtained for one variable is not related to or influenced by the second variable. This idea can be expressed in two versions:

• Version 1: A single sample is measured on two separate variables. For example, knowing your personality will help predict your color preference (alternative). Knowing your personality will NOT help you predict your color preference (null) [Personality and color preference are measured per person]
  • Null: The variables are not related.
  • Alternative: The variables are related.
• Version 2: Two (or more) samples are measured and compared to see if there are differences. For example, the same proportions of extroverts (group 1) and introverts (group 2) prefer the same color (null). If the proportions are different for the two groups, then you have the alternative hypothesis
  • Null: The samples are independent
  • Alternative: The samples are not independent

Here we are working with Version 1 (one group taking two types of items)

• \(H_0:\) The item difficulty is not related to how a person changes their answer
• \(H_1:\) The item difficulty is related to how a person changes their answer

Find Expected Frequencies

This is little more complex than the goodness of fit test

Step 1: Find row/col sums

Frequency	Right to Wrong	Wrong to Right	Sum
Easy	97	411	508
Difficult	251	620	871
Sum	348	1031	1379

Step 2: Expected frequencies per cell

\[f_e = \frac{col\,total*row\,total}{overall\,total}\]

Frequency	Right to Wrong	Wrong to Right	Sum
Easy	97 (128.1972)	411 (379.8028)	508
Difficult	251 (219.8028)	620 (651.1972)	871
Sum	348	1031	1379

Test of Independence Calculation by Hand

\[\chi^2 = \sum \frac{(f_o-f_e)^2}{f_e}\]

\(\chi^2 = \frac{(97-128.1972)^2}{128.1972} + \frac{(411-379.8028)^2}{379.8028} +\frac{(251-219.8028)^2}{219.8028}+\frac{(620-651.1972)^2}{651.1972}\)

\(\chi^2 = 16.08\)

Test Against Distribution

\(df = (Row-1)(Col-1)\) \(df = (2-1)(2-1) = 1\)

Given our \(df = 1\). We calculated 16.08 we can use R or a table to get the critical values for alpha = .05

Crit.MCQ=qchisq(.05, df=1, lower.tail = FALSE)

We get the crit = 3.8414588 < 16.08, so we reject the null.

Test of Independence Calculation by Code

Step 1: Build Your table

MCQ.Study.2 <- as.table(rbind(c(97, 411), c(251, 620)))
dimnames(MCQ.Study.2) <- list(Social = c("Easy","Diff"),
                              Change = c("RtoW", "WtoR"))
                             
MCQ.Study.2

##       Change
## Social RtoW WtoR
##   Easy   97  411
##   Diff  251  620

Step 2: Calculate chi-square

In tests of independence, it will calculate the expected frequencies for you. Also, you can apply a correction called the Yates’ continuity correction which reduced the error of when looking up discrete values on the continuous chi-square distribution. You should always use this version of the formula as it will be more conservative. You would simply write Yates corrected chi-square tests in your method section (no one uses the subscript as I wrote below).

\[\chi^2_{Yates} = \sum \frac{(|f_o-f_e| - .5)^2}{f_e}\]

Note: you can view observed and expected frequencies. Also, you can simulate the results as we did before.

(MCQ.chi.2 <- chisq.test(MCQ.Study.2,correct = TRUE))
MCQ.chi.2$observed   # observed counts (same as M)
MCQ.chi.2$expected   # expected counts under the null

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  MCQ.Study.2
## X-squared = 15.566, df = 1, p-value = 7.968e-05
## 
##       Change
## Social RtoW WtoR
##   Easy   97  411
##   Diff  251  620
##       Change
## Social     RtoW     WtoR
##   Easy 128.1972 379.8028
##   Diff 219.8028 651.1972

Step 3: Effect size

Biased calculation phi (\(\varphi\)) and cohen’s w can be estimated using this same formula (which is needed for power analysis). These are basically correlation coefficients when you have a 2x2 contingency table.

\[\varphi = \sqrt\frac{\chi^2}{N}\]

Cramer’s V, which is similar (\(\varphi\)), but used for when you have large than 2x2 tables.

\[V = \sqrt\frac{\chi^2}{N*min(C-1, R-1)}\]

\(V = \sqrt\frac{15.566}{1379*1} = 0.106283\)

df	Small	Medium	Large
1	0.10	0.30	0.50
2	0.07	0.21	0.35
3	0.06	0.17	0.29
4	0.05	0.15	0.25
5	0.04	0.13	0.22

Odd-Ratio (OR) as Effect size

Some people (mostly in the clinical) prefer odds ratios, but they can only work when you have a r X 2 table

Odds Ratio (OR) is a measure of association between exposure and an outcome.

Frequency	Right to Wrong	Wrong to Right
Easy	97 (A)	411 (B)
Difficult	251 (C)	620 (D)

Conceptually:

\[OR = \frac{AD}{BC}\]

\(OR = \frac{97*620}{411*251} = 0.58\)

So, people are .58 times more likely to switch from right-to-wrong/wrong-to-right based on the difficulty of the item. (OR < 1, so it’s less likely to happen). The item difficulty is significant as we already saw, but the difficulty has minimal impact.

In practice, we can use a package, which has other versions which can apply corrections and give us CIs around OR.

library(epitools)
# Regular
oddsratio.wald(MCQ.Study.2, correction=TRUE)$measure
# Small samples
oddsratio.small(MCQ.Study.2, correction=TRUE)$measure

##       odds ratio with 95% C.I.
## Social  estimate     lower     upper
##   Easy 1.0000000        NA        NA
##   Diff 0.5829722 0.4470703 0.7601862
##       odds ratio with 95% C.I.
## Social  estimate     lower     upper
##   Easy 1.0000000        NA        NA
##   Diff 0.5792495 0.4485089 0.7619142

Step 4: Report in APA

\(\chi^2(df,N) = X.XX, p < |= .XXX, V = .XX | OR = X.XX\)

Since our result was p-value < 7.968e-05

The item difficulty is related to how a person changes their answer, \(\chi^2(1,1379) = 15.57, p < .0001, V = .11\). [That is all we can say statistically. Normally people present a table in percentages to unpack this result, but You have to decide if you want to do row or column percentages. People do not present both]. I think the row percent make more sense in this case we want to compare across item difficulty.

Row Proportion Code

prop.table(MCQ.Study.2,1)

% Row	Right to Wrong	Wrong to Right	%
Easy	19.1%	80.9%	100%
Difficult	28.8%	71.2%	100%
Col Total	25.2%	74.8%	100%

Col Proportion Code

prop.table(MCQ.Study.2,2)

% Col	Right to Wrong	Wrong to Right	Row Total
Easy	27.9%	39.9%	36.8%
Difficult	72.1%	60.1%	63.2%
%	100%	100%	100%

Chi-Square Issues

• We must have at least five responses per cell (it will calculate but its an assumption of the test)
• Chi-squared cannot be negative because all discrepancies are squared.
• Chi-squared can be zero, but only in the unusual event that each observed frequency exactly equals the corresponding expected frequency.
• Other things being equal, the larger the discrepancy between the expected frequencies and their corresponding observed frequencies, the larger the observed value of chi-square.
• It is not the size of the discrepancy alone that accounts for a contribution to the value of chi-square, but the size of the discrepancy relative to the magnitude of the expected frequency.
• The value of chi-square depends on the number of discrepancies involved in its calculation.
• There is no follow-up method, so we can remove conditions and re-test our chi-square (or one one-way chi-square), but you will need to Bonferroni correct the pvalues by hand (pvalue X number of tests conducted).
• High rate of Type II error

Power in Chi-Squared

Let’s use our use the V we got in the study above to substitute for Cohen’s W. Let’s use the power package to solve for N (total # of observations needed)

library(pwr)
pwr.chisq.test(w = 0.106283, N = NULL, df = 1, sig.level = 0.05, power = .80)

## 
##      Chi squared power calculation 
## 
##               w = 0.106283
##               N = 694.8307
##              df = 1
##       sig.level = 0.05
##           power = 0.8
## 
## NOTE: N is the number of observations

Other Classical Non-Parametric Tests

Nominal Data:

• Chi-square test is the non-parametric equivalent to z, t, or F tests, but for nominal data only!
  • Binomial/sign test is a special case of the Chi-squared
  • Another older alternative is Fisher’s Exact test

Fisher’s Exact test

Fisher’s Exact test is like a chi-square, but its calculated differently and can be more conservative than Pearson’s chi-square. Its often used when you have small cell sizes.

fisher.test(MCQ.Study.2, simulate.p.value = TRUE, B = 1e5)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  MCQ.Study.2
## p-value = 6.496e-05
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.4421001 0.7654197
## sample estimates:
## odds ratio 
##  0.5831962

Binominal Data

The binomial distribution approaches a normal distribution as you add more trials (for example, the more coin flips you have the more normal the distribution looks; where p=prob of head, and q=prob of tails, n = coin flips). Generally, when the values of pn and qn are both equal to 10, the distribution approaches normal. Note: \(\mu=pn\), \(\sigma = \sqrt{npq}\). Note this test is an old test useful when people tended to do stats by hand.

\[Z = \frac{X-\mu}{\sigma} = \frac{X-pn}{\sqrt{npq}}\]

We can use our Zcrit table again (remember \(\alpha=.05\) yields \(Z_{crit} = 1.96\))

Let’s use our goodness of fit data again:

Frequency	Right to Wrong	Wrong to Right
Observed	27	195

Binomial by hand

We just need to call one of the conditions a “success” (we will pick Wrong-to-Right; \(X = 195\)). So \(p = .5\), \(q = .5\), Our \(n = 195+27 = 222\)

\(Z = \frac{195-.5*222}{\sqrt{222*.5*.5}} = 11.27542\)

\(Z = 11.28, p < .05\)

Note: \(Z^2 = \chi^2\) = 11.27542^2 = 127.14 (the one-way \(\chi^2\) value we got above!)

Binomial by R function

binom.test(195, 222, p = 0.5,
           conf.level = 0.95)

## 
##  Exact binomial test
## 
## data:  195 and 222
## number of successes = 195, number of trials = 222, p-value < 2.2e-16
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.8279981 0.9182995
## sample estimates:
## probability of success 
##              0.8783784

Sign test

• Sign test is a special case of the binomial test
• A sign test compares the number of times a treatment results one direction over another.
  • Example, let’s say that you were a therapist charting several of your patient’s improvement to a new type of therapy you were using. You cannot measure the magnitude of the improvement, but you can record if you see if they improve or get worse.
    Sign tests:
• Are used when you have the direction of change from an experiment
• Can be used as a pilot test to see if you should move forward in an experiment
• Can support a hypothesis when all other tests fail
• Are not as sensitive as parametric tests
• Use the same calculation as the binomial test; you just count the number of pluses and minuses

Ordinal Data

Wilcoxon rank sum test

Non-parametric equivalent to the t-test. This test compares ranks and not the means. It comes in two flavors (paired-sample and independent sample [also called the Mann-Whitney U-test])

Wilcoxon rank sum test for independent sample

\(H_0:\) There is no difference between the two treatments.

• Therefore, there is no tendency for the ranks of one treatment condition to be systematically higher or lower than the ranks for the other treatment.

\(H_1:\) There is a difference between the two treatments.

• Therefore, the ranks in one treatment condition are systematically higher or lower than the ranks in another treatment.

Group 1	Group 2
41	10
39	14
37	9
44	17
40	12
45	8
46	104

Data frame in R

data.W<-data.frame(IV=c(rep("G1",7),rep("G2",7)),
                        DV =c(41,39,37,44,40,45,46,10,14,9,13,12,8,104))

Independent t-test

library(dplyr)
data.W %>% group_by(IV) %>% summarise(Mean=mean(DV), SD=sd(DV))
t.test(DV~IV,data=data.W, paired=FALSE)

## # A tibble: 2 × 3
##   IV     Mean    SD
##   <chr> <dbl> <dbl>
## 1 G1     41.7  3.35
## 2 G2     24.3 35.2 
## 
##  Welch Two Sample t-test
## 
## data:  DV by IV
## t = 1.3035, df = 6.1087, p-value = 0.2394
## alternative hypothesis: true difference in means between group G1 and group G2 is not equal to 0
## 95 percent confidence interval:
##  -15.14833  50.00547
## sample estimates:
## mean in group G1 mean in group G2 
##         41.71429         24.28571

Independent W-test

wilcox.test(DV~IV,data=data.W, paired=FALSE)

## 
##  Wilcoxon rank sum exact test
## 
## data:  DV by IV
## W = 42, p-value = 0.02622
## alternative hypothesis: true location shift is not equal to 0

In this case, by comparing ranks and not raw scores, we can see the non-parametric test gives a significant result (as we are comparing ranks the variance difference between the groups goes away)

Note: If the data is paired sample, you simply have to say paired=TRUE

Paired W-test

t.test(DV~IV,data=data.W, paired=TRUE)
wilcox.test(DV~IV,data=data.W, paired=TRUE, alternative =("two.sided"))

## 
##  Paired t-test
## 
## data:  DV by IV
## t = 1.3777, df = 6, p-value = 0.2175
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -13.52663  48.38378
## sample estimates:
## mean difference 
##        17.42857 
## 
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  DV by IV
## V = 21, p-value = 0.2702
## alternative hypothesis: true location shift is not equal to 0

Kruskal-Wallis Test

The non-parametric equivalent to the independent measures one-way ANOVA. It compares three or more separate groups and is tested against the chi-square distribution.

Like the W test, you would convert the data into ranks and calculate the H value.

Group 1	Group 2	Group 3
14	2	26
3	14	8
2	9	14
5	12	19
8	5	20

Data frame in R

data.H<-data.frame(IV=c(rep("G1",5),rep("G2",5),rep("G3",5)),
                        DV =c(14,3,2,5,8,
                              2,14,9,12,5,
                              26,8,14,19,20))

Kruskal-Wallis Test in R

kruskal.test(DV~IV, data=data.H) 

## 
##  Kruskal-Wallis rank sum test
## 
## data:  DV by IV
## Kruskal-Wallis chi-squared = 6.0608, df = 2, p-value = 0.0483

You can follow up this analysis with the W test above

Friedman Test

Non-parametric one-way RM ANOVA. For this test you must have a “block”. You block will be your ID variable. You can follow up this test with Wilcoxon rank sum test (paired=TRUE).

ID	Group 1	Group 2	Group 3
1	14	2	26
2	3	14	8
3	2	9	14
4	5	12	19
5	8	5	20

Data frame in R

data.F<-data.frame(ID=rep(1:5,3),
                   IV=c(rep("G1",5),rep("G2",5),rep("G3",5)),
                        DV =c(14,3,2,5,8,
                              2,14,9,12,5,
                              26,8,14,19,20))

Friedman Test in R

friedman.test(DV~IV|ID, data=data.F) 

## 
##  Friedman rank sum test
## 
## data:  DV and IV and ID
## Friedman chi-squared = 5.2, df = 2, p-value = 0.07427

You can follow up this analysis with the W test above

Pros and Cons

Classical non-parametrics are easy to run by hand and are often useful if parametric tests fail (especially if you have large variance or suspect your assumptions are not being met). However, they have a high rate of Type II Error.

References

Best, J, B. (1979). Item difficulty and answer changing. Teaching of Psychology, 6, 228-230