Non-Linear Models

What does Linearity & Non-Linearity Mean?

• The majority of psychologists often use these terms to describe the relationship between Y~X
  • Linearity = mathematical relationship between variables can be fit with a straight line
  • Non-Linear (Curvilinear) = mathematical relationship between variables can be fit with non-straight (Curvy) lines
    • However, be careful as for other fields or specialty areas of psychology these terms can mean different things: When people say non-linear, ask them what they mean

Non-Linear Fit Types that can be transformed into linear regression (basic types)

• Polynomials: Power & Orthogonal
• Growth: Exponential, Power, Logarithmic
• Rates: Reciprocal
• Correlations

Power Polynomials

• Models that simply curves, such as quadratic or cubic effects
  
• Linear: \(Y =B_{1}X + B_0\)
• Quadratic: \(Y = B_{1.2}X + B_{2.1}X^2 + B_0\)
• Cubic: \(Y = B_{1.23}X + B_{2.13}X^2 + B_{3.12}X^3 + B_0\)

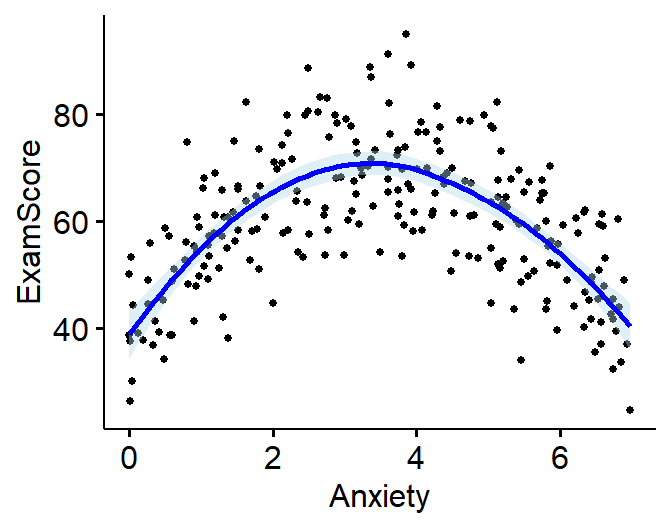
Simulate a Exam Score ~ Anxiety

\(Y = 17.5X -2.5X^2 + 40 + \epsilon\)

Where, \(X\) = Uniform distribution of Likert scores between 0 to 7 (0 = No anxiety) & \(\epsilon\) = Random Normal [\(M = 0\) & \(S=10\)]

set.seed(42)    
n <- 250 # 250 people
x <- runif(n, 0, 7)
# Our equation to create Y
y <- -2.5*x^2 + 17.5*x+40+rnorm(n, sd=10)
#Build our data frame
Quad.Data<-data.frame(Anxiety=x,ExamScore=y)

Visualize Simulation/Data

Beyond visualizing the scatter plot, we need some way to estimate if the effect might be linear or non-linear

Loess Line

LOESS = Locally Weighted Scatterplot Smoothing

Does lots of regressions on small sections of the scatter plot to get the best fit (curvy) line. Allows you visualize complex relationships, but it can overfit the relationship (so be careful. Thus its a good diagnostic tool, but rarely used in papers.

library(ggpubr) #graph data
ggscatter(Quad.Data, x = "Anxiety", y = "ExamScore",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

Fitting Power Polynomials

Forward Selection Approach

• Model \(1\): Linear fit
• Model \(2\): Quadratic fit
• Check the change in \(R^2\) and select the best fit models
• Model \(i\): keep going up until you are satisfied
  • Note: Higher order terms ALWAYS increase \(R^2\), you need to make sure it is both a significant improvement and meaningful improvement
  • in R there are two ways to add Power Polynomials: I(Term^2) or using the poly command

#Linear model
Model.1<-lm(ExamScore~Anxiety, data= Quad.Data)
#Quad model
Model.2<-lm(ExamScore~Anxiety+I(Anxiety^2), data= Quad.Data)

• Test to see if the model is improved by the new term

anova(Model.1,Model.2)

## Analysis of Variance Table
## 
## Model 1: ExamScore ~ Anxiety
## Model 2: ExamScore ~ Anxiety + I(Anxiety^2)
##   Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
## 1    248 43354                                  
## 2    247 21319  1     22036 255.31 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Examine model paramaters

	Dependent variable:
	ExamScore
	Linear	Quadratic
	(1)	(2)
Constant	60.333*** (1.686)	39.681*** (1.753)
Anxiety	-0.137 (0.411)	17.753*** (1.156)
I(Anxiety2)		-2.559*** (0.160)
Observations	250	250
R2	0.0004	0.508
Adjusted R2	-0.004	0.505
Residual Std. Error	13.222 (df = 248)	9.290 (df = 247)
F Statistic	0.111 (df = 1; 248)	127.767*** (df = 2; 247)
Note:	p<0.1; p<0.05; p<0.01

• The change in \(R^2\) = 0.5080438 and we can see that the change was significant
• Would the third order term be any better?

#Cubic model
Model.3<-lm(ExamScore~Anxiety+I(Anxiety^2)+I(Anxiety^3), data= Quad.Data)
anova(Model.1,Model.2,Model.3)

## Analysis of Variance Table
## 
## Model 1: ExamScore ~ Anxiety
## Model 2: ExamScore ~ Anxiety + I(Anxiety^2)
## Model 3: ExamScore ~ Anxiety + I(Anxiety^2) + I(Anxiety^3)
##   Res.Df   RSS Df Sum of Sq        F Pr(>F)    
## 1    248 43354                                 
## 2    247 21319  1   22035.8 255.0382 <2e-16 ***
## 3    246 21255  1      63.8   0.7378 0.3912    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

	Dependent variable:
	ExamScore
	Linear	Quadratic	Cubic
	(1)	(2)	(3)
Constant	60.333*** (1.686)	39.681*** (1.753)	38.386*** (2.312)
Anxiety	-0.137 (0.411)	17.753*** (1.156)	20.023*** (2.885)
I(Anxiety2)		-2.559*** (0.160)	-3.371*** (0.959)
I(Anxiety3)			0.077 (0.090)
Observations	250	250	250
R2	0.0004	0.508	0.510
Adjusted R2	-0.004	0.505	0.504
Residual Std. Error	13.222 (df = 248)	9.290 (df = 247)	9.295 (df = 246)
F Statistic	0.111 (df = 1; 248)	127.767*** (df = 2; 247)	85.333*** (df = 3; 246)
Note:	p<0.1; p<0.05; p<0.01

Second order power polynomial was our best fit

Model 2 in Detail

Since we simulated our model we know what the answers should be \(Y = 17.5X -2.5X^2 + 40 +\epsilon\)

• Extract our terms from our regression and compare to our simulated values.

IT<-round(Model.2$coefficients[1],2)
LT<-round(Model.2$coefficients[2],2)
QT<-round(Model.2$coefficients[3],2)

Regression estimated values: \(Y =\) 17.75\(X\) -2.56\(X^2 +\) 39.68 \(+\epsilon\)

• Our regression did a good job, but what if our sample was smaller?
• Redo our analysis with n = 5 to 60 and see how the terms change [see simulation in separate R file]
• the gray band = 95% CI

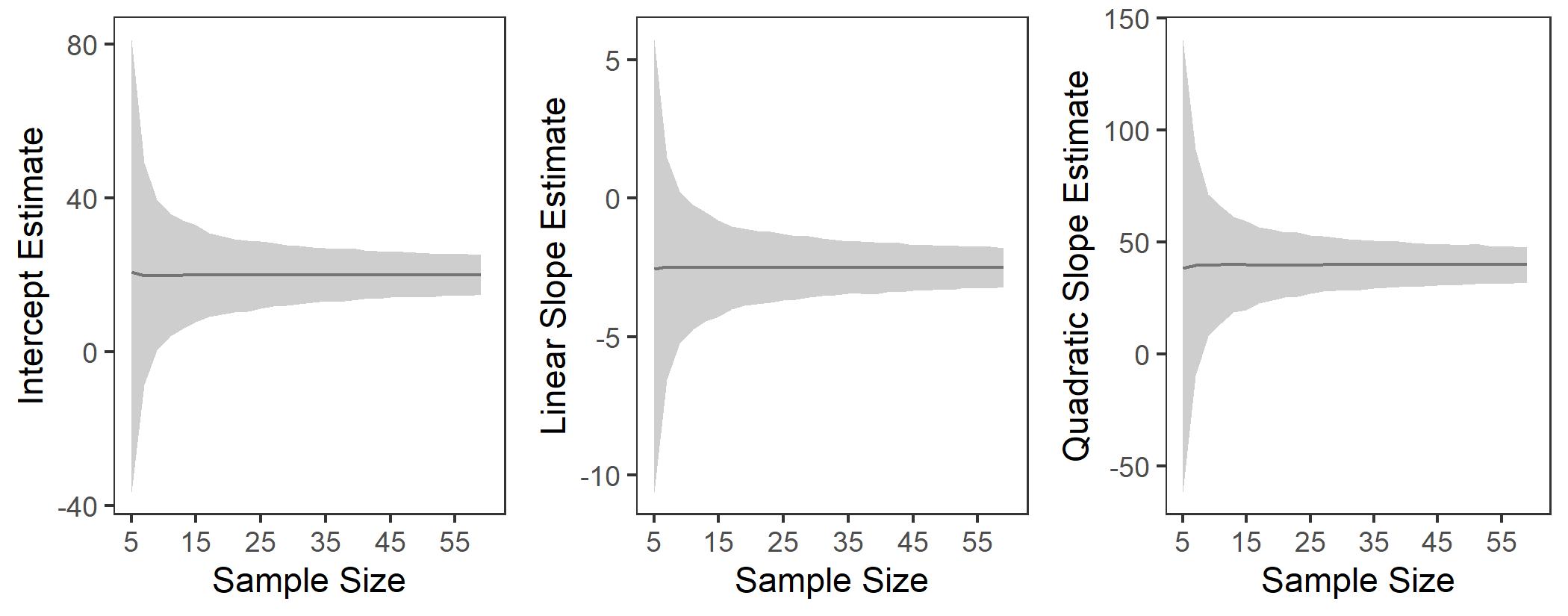
It’s important to know that in small samples polynomial estimates can be very unstable. Also note: If you flip the quadratic term, the line will flip direction!

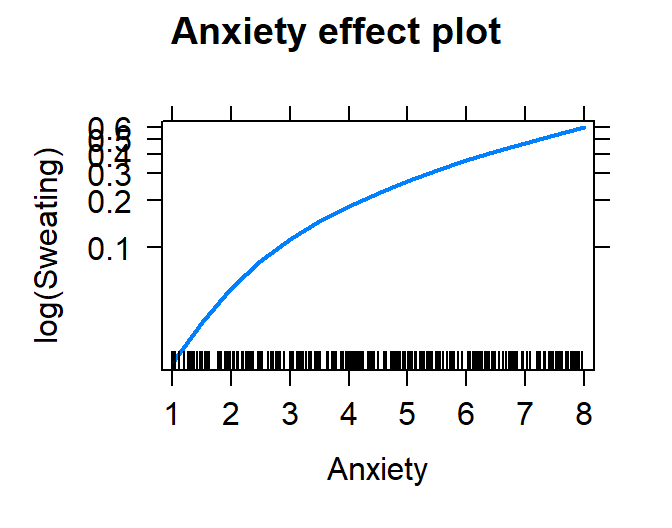
How to plot this function (and not the loess line)

• You can solve the regression equation for different values of x
• in R you can call the effects package to do work for you to solve the regression equation at different values of \(X\) [0 to 7].

library(effects)
plot(effect("Anxiety", Model.2,
            xlevels=list(Anxiety=seq(0,7,1))))

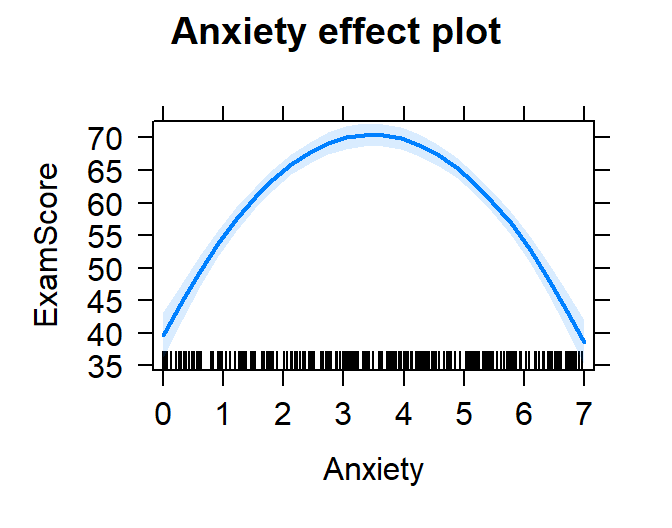
Code approach to power polynomials

You can use a command called poly which will do both power and orthogonal polynomials. But you cannot have missing data to use this code. The function has serval important arguments we will focus on: poly(x, degree = 1, raw = FALSE, simple=FALSE). degree = order number. So degree = 3 tests the linear, quadratic, and cubic. raw = FALSE tests the orthogonal versions. To keep them as power polynomials we must say raw = TRUE. Lastly, there is simple=FALSE, this is the default and keeps the attributes assigned the new vectors you have created. I suggest leaving this alone, meaning leave the default as is, but it is useful to know as sometimes when we pass the results of our model this can create problems with other packages (but I have yet to see this).

#Cubic model
Model.3.P<-lm(ExamScore~poly(Anxiety,3,raw=TRUE), data= Quad.Data)
summary(Model.3.P)

## 
## Call:
## lm(formula = ExamScore ~ poly(Anxiety, 3, raw = TRUE), data = Quad.Data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -25.7936  -6.7479  -0.0587   6.5252  24.9911 
## 
## Coefficients:
##                               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                   38.38640    2.31249  16.600  < 2e-16 ***
## poly(Anxiety, 3, raw = TRUE)1 20.02317    2.88488   6.941 3.44e-11 ***
## poly(Anxiety, 3, raw = TRUE)2 -3.37082    0.95900  -3.515 0.000523 ***
## poly(Anxiety, 3, raw = TRUE)3  0.07736    0.09006   0.859 0.391190    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.295 on 246 degrees of freedom
## Multiple R-squared:   0.51,  Adjusted R-squared:  0.504 
## F-statistic: 85.33 on 3 and 246 DF,  p-value: < 2.2e-16

Above you can see the names of the paramaters in the model have changed.

• poly(Anxiety, 3, raw = TRUE)1 = linear
• poly(Anxiety, 3, raw = TRUE)2 = quadratic
• poly(Anxiety, 3, raw = TRUE)3 = cubic.

Orthogonal Polynomials

Problem with Power polynomials is interpreting them independently. The higher order terms depend on, the lower order terms. Thus linear term can be significant cause the higher order term is significant, but there is no linear trend in the data (just like in today’s example). This is because power polynomials correlate with each other (they are are not unique predictors)

Linear.Values<-c(1,2,3,4,5,6,7)
Quad.Values<-Linear.Values^2

L.vs.Q<-data.frame(Linear.Values=Linear.Values,Quad.Values=Quad.Values)
ggscatter(L.vs.Q, x = "Linear.Values", y = "Quad.Values",
   add = "reg.line",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   size = 2 # Size of dots
   )

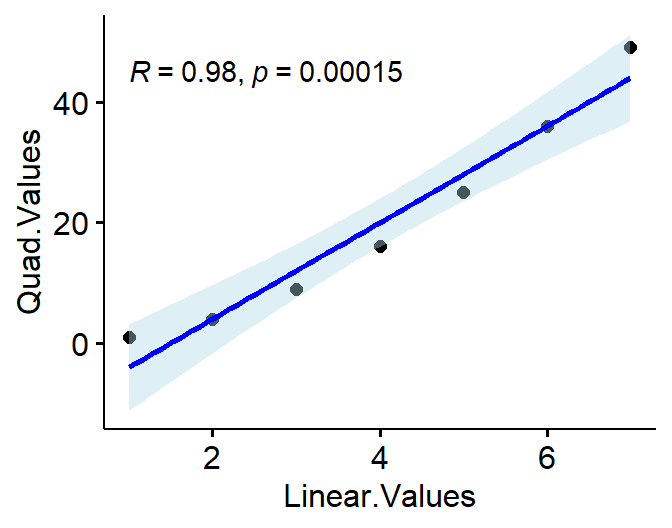
• Thus they are basically multicollinear
• Let’s run our VIF to verify

library(car)
vif(Model.2)

##      Anxiety I(Anxiety^2) 
##     16.05275     16.05275

Technically, it’s OK that they are multicollinear, but you cannot interpret each term without looking at the other (the p-values will be problematic).

• The solution to make the linear and quadratic terms correlate with each at zero (just as we did with ANOVA)
• We can use the poly code in R to make them Orthogonal.
• Here is an example of what R is going to do:

LinearTerms<-c(1,2,3,4,5,6,7)
#make them Orthogonal
O.Poly<-poly(LinearTerms,2)

L.vs.Q.Ortho<-data.frame(Linear.Values.Ortho=O.Poly[,1],Quad.Values.Ortho=O.Poly[,2])

ggscatter(L.vs.Q.Ortho, x = "Linear.Values.Ortho", y = "Quad.Values.Ortho",
   add = "reg.line",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = TRUE, # Add correlation coefficient. see ?stat_cor
   size = 2 # Size of dots
   )

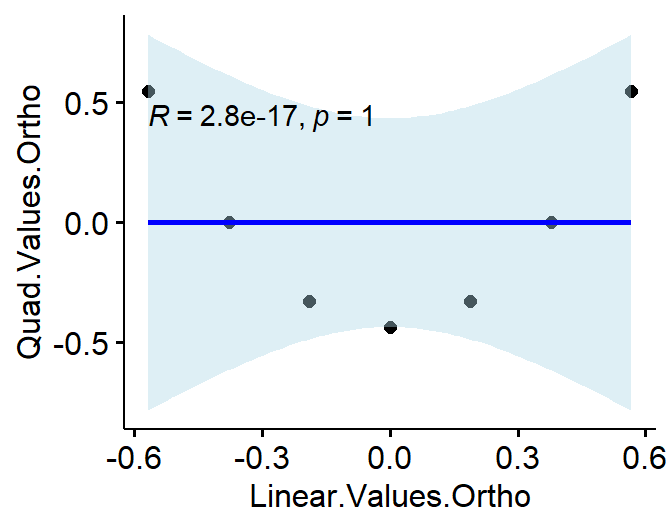
Correlation between linear and quadratic is now, r = 0!

#lets make a new poly vector
Model.1.O<-lm(ExamScore~poly(Anxiety, 1), data= Quad.Data)
Model.2.O<-lm(ExamScore~poly(Anxiety, 2), data= Quad.Data)

anova(Model.1.O,Model.2.O)

## Analysis of Variance Table
## 
## Model 1: ExamScore ~ poly(Anxiety, 1)
## Model 2: ExamScore ~ poly(Anxiety, 2)
##   Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
## 1    248 43354                                  
## 2    247 21319  1     22036 255.31 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

	Dependent variable:
	ExamScore
	Linear.Ortho	Quadratic.Ortho
	(1)	(2)
Constant	59.845*** (0.836)	59.845*** (0.588)
poly(Anxiety, 1)	-4.403 (13.222)
poly(Anxiety, 2)1		-4.403 (9.290)
poly(Anxiety, 2)2		-148.444*** (9.290)
Observations	250	250
R2	0.0004	0.508
Adjusted R2	-0.004	0.505
Residual Std. Error	13.222 (df = 248)	9.290 (df = 247)
F Statistic	0.111 (df = 1; 248)	127.767*** (df = 2; 247)
Note:	p<0.1; p<0.05; p<0.01

• Notice that the linear term is not significant, but the quadratic is
  • but the actual estimate of the slopes are nonsensical
• This is because you have rescaled the x-values in a funny way (see plot above)
  • But no more multicollinearity
• Let’s run our VIF to verify
  • Note: poly gets read to vif as one factor, so I will manually enter these into the model

Quad.Data$Anxiety.O.1<-poly(Quad.Data$Anxiety,2)[,1]
Quad.Data$Anxiety.O.2<-poly(Quad.Data$Anxiety,2)[,2]
Model.2.O.2<-lm(ExamScore~Anxiety.O.1+Anxiety.O.2, data= Quad.Data)
vif(Model.2.O.2)

## Anxiety.O.1 Anxiety.O.2 
##           1           1

• Also the \(R^2\) do not differ between the power or orthogonal polynomials
• Other pros of using orthogonal polynomials will come when we start looking at interactions

Coding shortcut (Use this for your analysis)

• You don’t need to premake the vector as I did above
• You can put the poly code right into the model
  • but the labeling will change
• Also much easier to makes plots of the final model this way

Model.2.O.S<-lm(ExamScore~poly(Anxiety,2), data= Quad.Data)

	Dependent variable:
	ExamScore
	Quadratic.Ortho
Constant	59.845*** (0.588)
poly(Anxiety, 2)1	-4.403 (9.290)
poly(Anxiety, 2)2	-148.444*** (9.290)
Observations	250
R2	0.508
Adjusted R2	0.505
Residual Std. Error	9.290 (df = 247)
F Statistic	127.767*** (df = 2; 247)
Note:	p<0.1; p<0.05; p<0.01

The effects package will “know” you used poly command and convert the results back for you automatically

plot(effect("poly(Anxiety,2)", Model.2.O.S,
           xlevels=list(Anxiety=seq(0,7,1))))

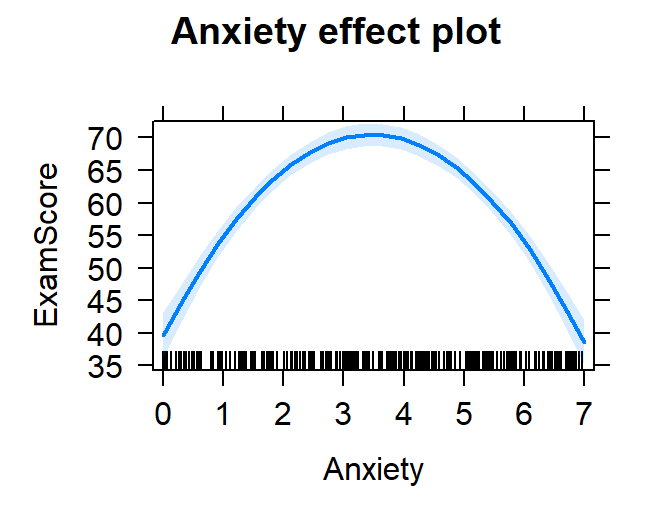
• Also, you could have said poly(Anxiety,2,raw=TRUE) to get Power polynomial on the fly

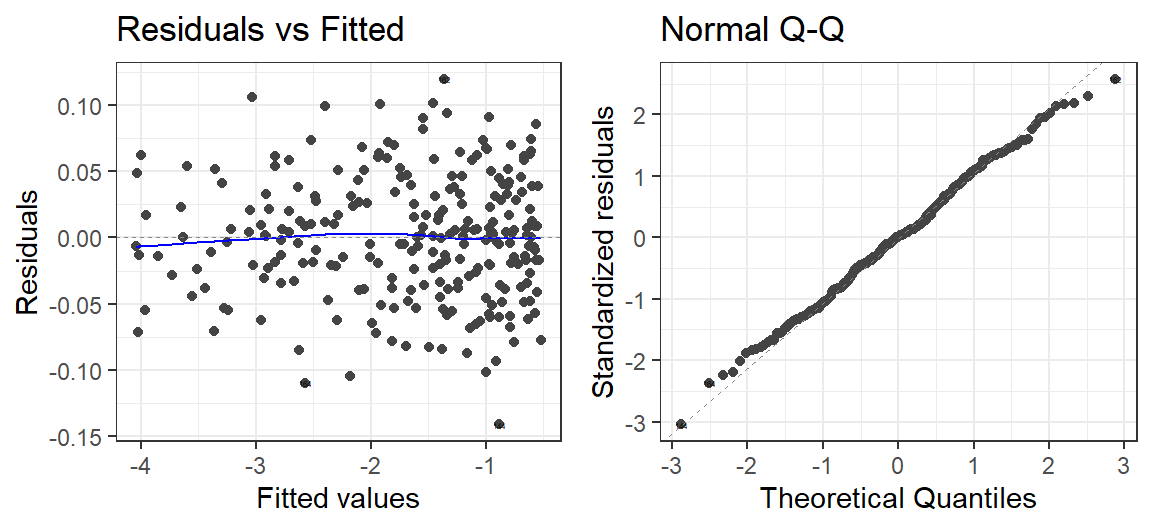
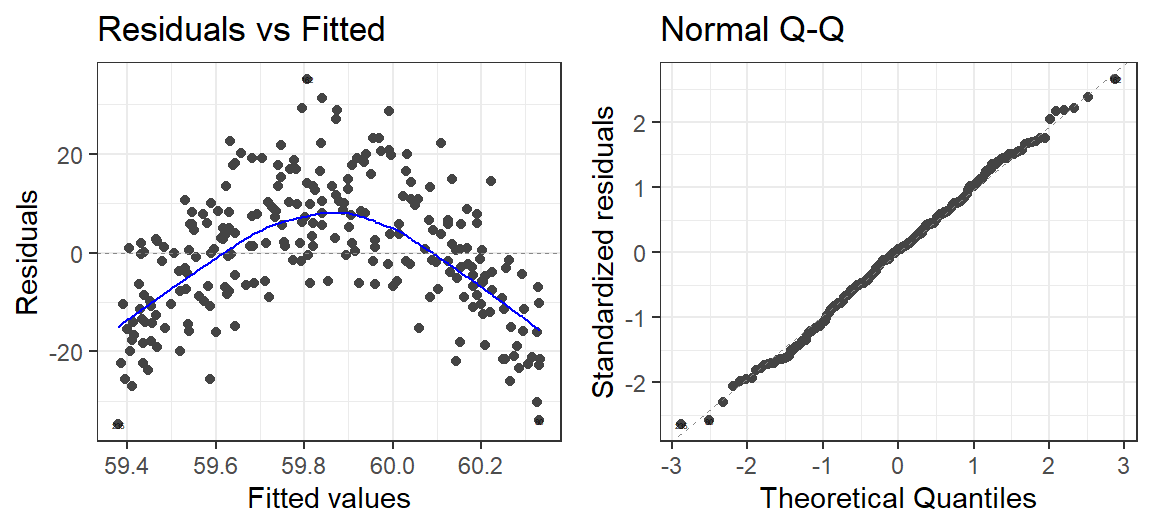
Diagnostics

• When you have the wrong number of polynomials you will get funny looking residuals

library(ggfortify)
autoplot(Model.1, which = 1:2, label.size = 1) + theme_bw()

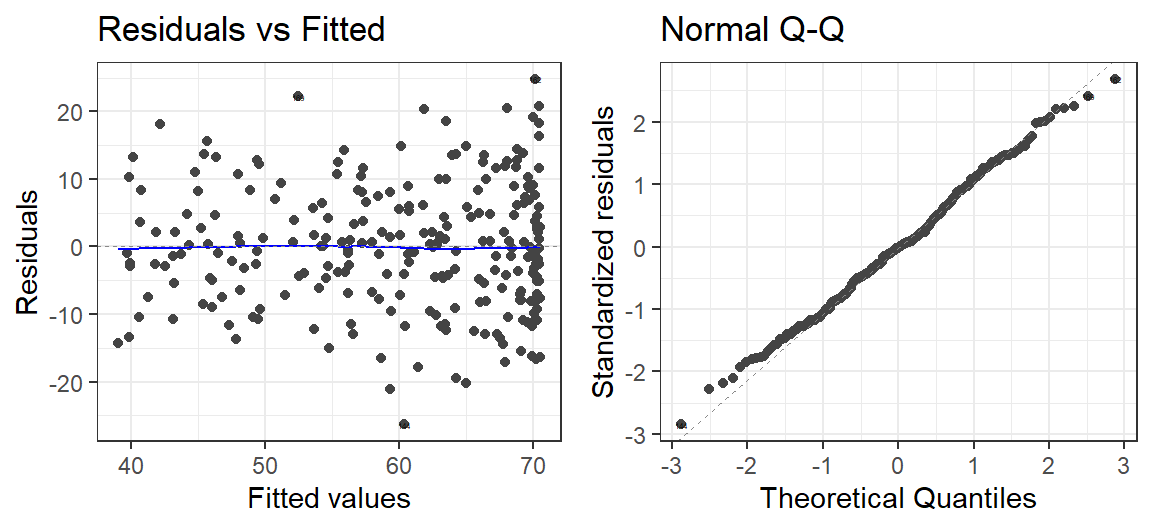
• When you have the right number of polynomials, you will get correct looking residuals
• Here is when we use 2 when we need 2

autoplot(Model.2.O.S, which = 1:2, label.size = 1) + theme_bw()

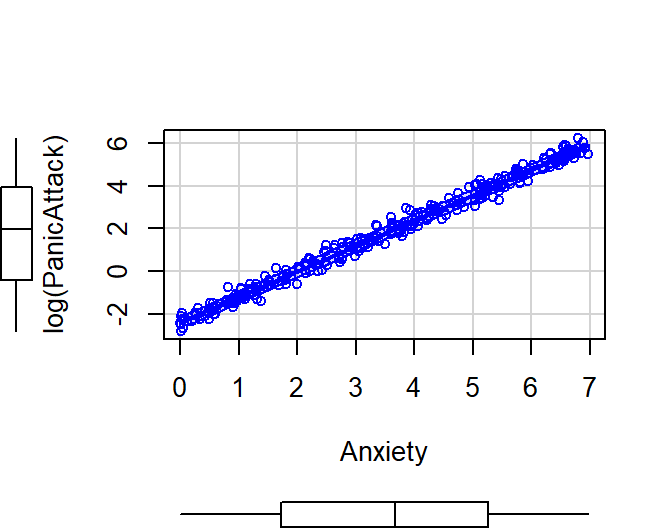
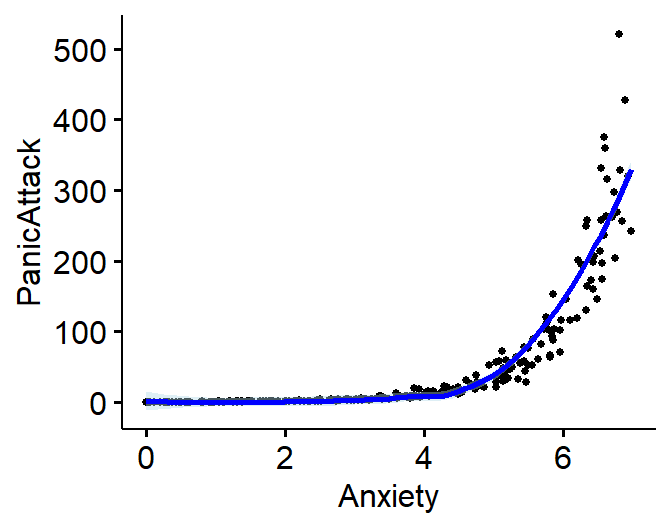
Dealing Growth Curves (Part 2)

• These are models that cannot be fit with polynomials
• Exponential growth: \(Y = ce^{dx}\)
• Severity of panic attack (0 to 500) predicted by anxiety level
• Exponential Example: \(Y = .09e^{1.2x+\epsilon}\)
• Note: Euler’s number, \(e =\) 2.7182818, is an irrational math constant and the base value of the natural log

set.seed(42)
n <- 250
x <- runif(n, 0, 7)
#lets make our e value (not the error term)
e<-exp(1)
y <-.09*e^(1.20*(x+rnorm(n, sd=.25)))
Exp.Data<-data.frame(Anxiety=x,PanicAttack=y)

ggscatter(Exp.Data, x = "Anxiety", y = "PanicAttack",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

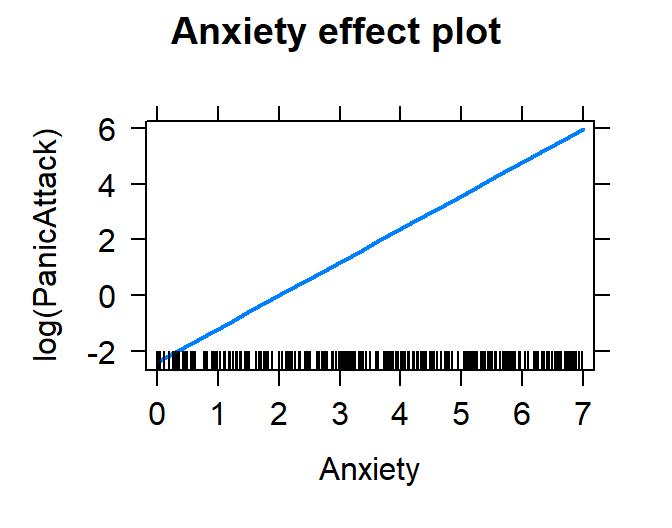
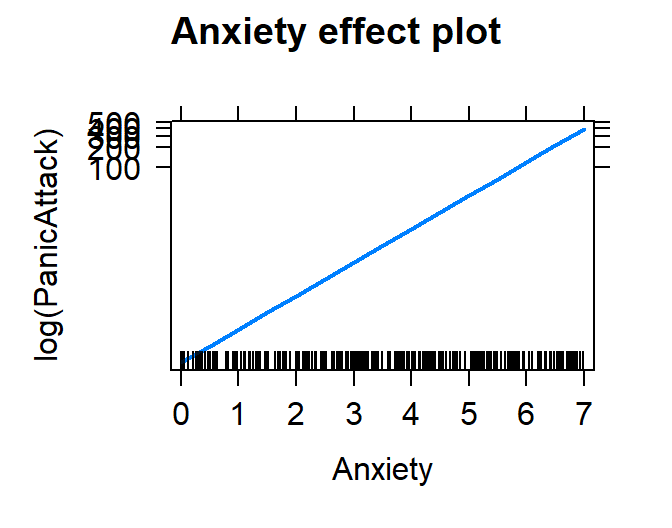
Do Polynomials fail us?

• Let’s try a second order fit since it one curve

Model.Panic.Poly<-lm(PanicAttack~poly(Anxiety,2), data= Exp.Data)

	Dependent variable:
	PanicAttack
	Quadratic.Ortho
Constant	50.000*** (2.515)
poly(Anxiety, 2)1	1,006.757*** (39.762)
poly(Anxiety, 2)2	772.384*** (39.762)
Observations	250
R2	0.805
Adjusted R2	0.803
Residual Std. Error	39.762 (df = 247)
F Statistic	509.199*** (df = 2; 247)
Note:	p<0.1; p<0.05; p<0.01

• Using the poly right into the package can be useful for the effects package because we can now view independent impact of the linear and quadratic terms

plot(effect("poly(Anxiety,2)", Model.Panic.Poly,
           xlevels=list(Anxiety=seq(0,7,1))))

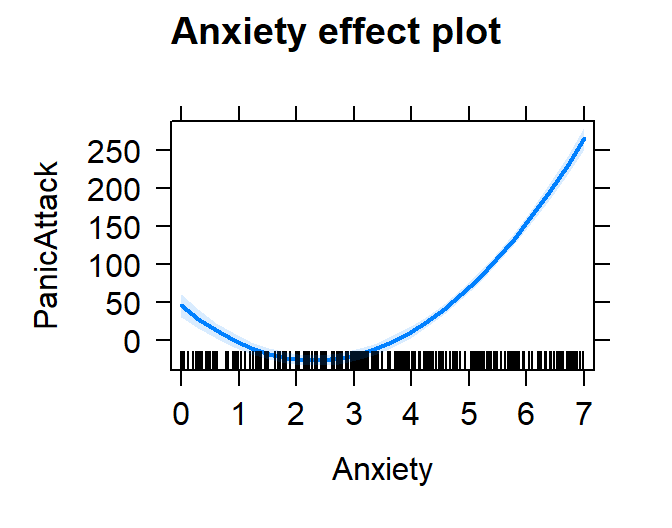- Yikes, based on this you might tell people having zero anxiety is worse than having lower anxiety

• Let check the residuals

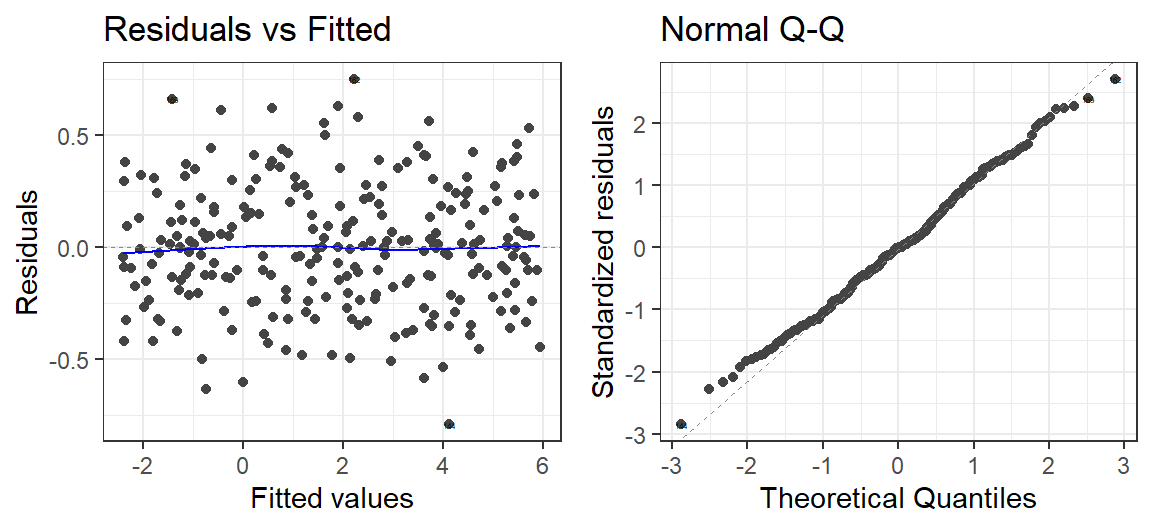
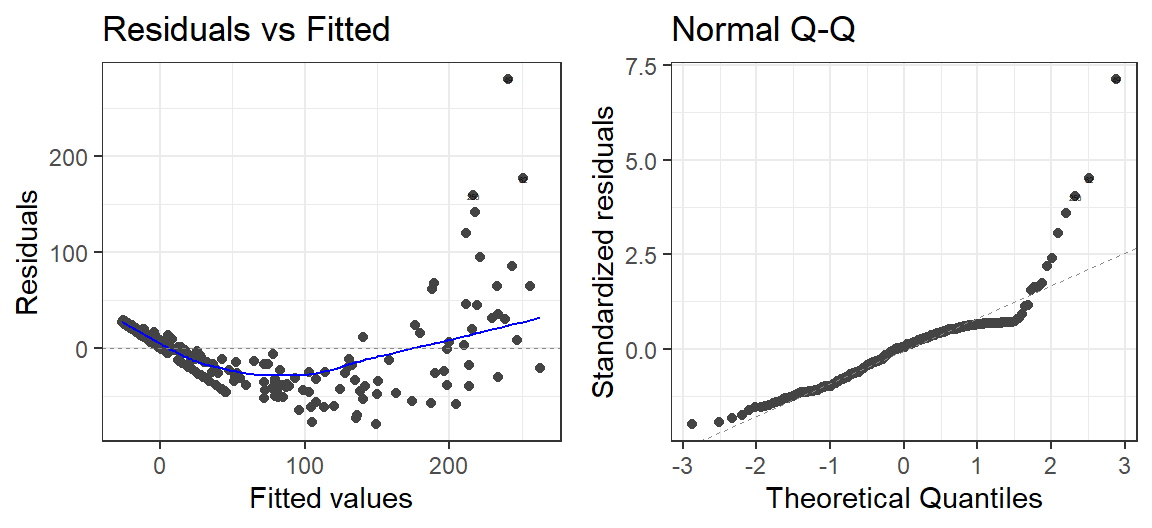
autoplot(Model.Panic.Poly, which = 1:2, label.size = 1) + theme_bw()

• Also looks pretty odd

Transformations of Exponential Model

• The solution to this problem is often to transform the offending variable
• The type of transform depends on the type of growth model you have
• Exponential model: Dependent variable = log(y) [in r, log = natural log]
• Thus: \(log(Y) = B_0 + BX\)
• And to convert from log into meaningful values:
• \(Y = e^{B_0 + BX}\)
• Let’s look at Log(Y) by Anxiety [we will use the scatterplot function in car package to see this more quickly]

library(car)
scatterplot(log(PanicAttack)~Anxiety, data= Exp.Data)

• Looks like a line now
• Let’s look at the model fit

Model.Panic.Log<-lm(log(PanicAttack)~Anxiety, data= Exp.Data)

	Dependent variable:
	log(PanicAttack)
Constant	-2.403*** (0.035)
Anxiety	1.195*** (0.009)
Observations	250
R2	0.987
Adjusted R2	0.987
Residual Std. Error	0.278 (df = 248)
F Statistic	19,129.080*** (df = 1; 248)
Note:	p<0.1; p<0.05; p<0.01

Plot the fit

plot(effect("Anxiety", Model.Panic.Log,
           xlevels=list(Anxiety=seq(0,7,1))))

You can plot it non-log units (to unlog use exp function), but you have to tell the package to convert it back to raw score.

plot(effect("Anxiety", Model.Panic.Log,
          transformation=list(link=log, inverse=exp)))

Plot the fit and check the residuals

autoplot(Model.Panic.Log, which = 1:2, label.size = 1) + theme_bw()

Those look as they should.

Challenge of Working with Transforms

• Problem is our scores are in log (not raw score)
• to convert from log into meaningful values:
• \(Y = e^{B_0 + BX}\)

#Intercept
IT.L<-round(Model.Panic.Log$coefficients[1],2)
#slope
LT.L<-round(Model.Panic.Log$coefficients[2],2)

• \(Y = e\)^(-2.4 + 1.2X)
• For Anxiety score of X = 0, Y = 0.090718
• For Anxiety score of X = 4, Y = 11.0231764
• For Anxiety score of X = 7, Y = 403.4287935
• [Note: Be careful about which log you use (natural or base 10, you can use either but make sure to specify)]

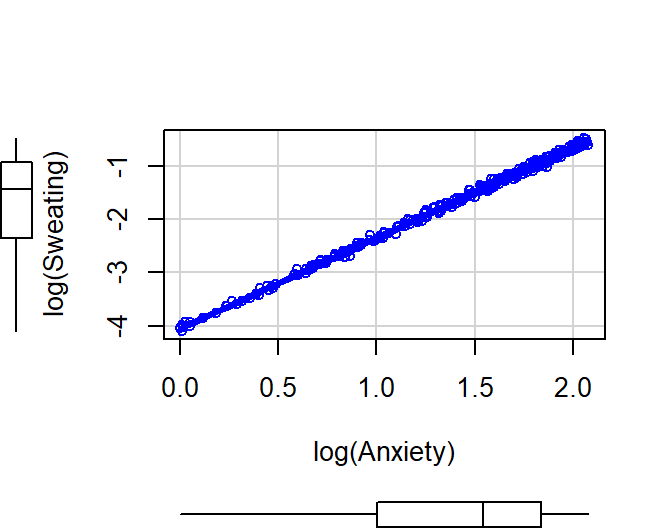
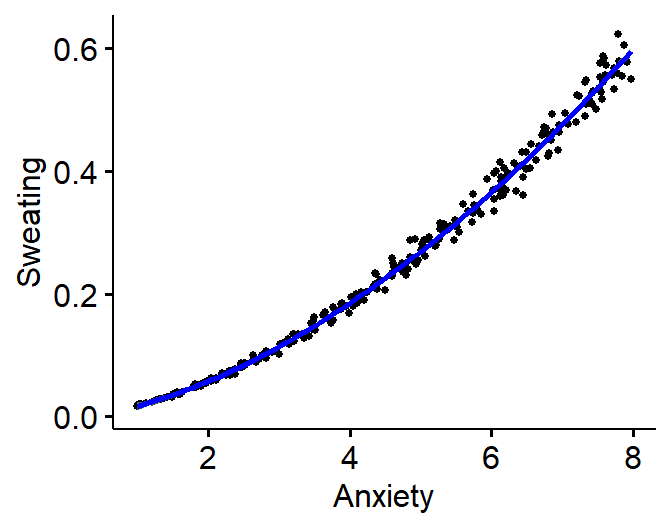
Power law

• Common function in motor control and perception experiments
• \(Y = cX^d\)
• Severity of sweating (0 to 100) predicted by anxiety level
• Exponential Example: \(Y = .07(X)^{1.7}+\epsilon\)
• Note: Natural log of 0 = -inf, so if you have zeros you need to always add 1

set.seed(42)
n <- 250
x <- runif(n, 0, 7)+1
y <-.07*(x)^1.7
y = y * (.05* (5+rnorm(n, sd=.25)))
Power.Data<-data.frame(Anxiety=x,Sweating=y)

ggscatter(Power.Data, x = "Anxiety", y = "Sweating",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

Transformations of Power Law

• The solution to this problem is often to transform the offending variable
• Power law model: DV and IV get logged: log(y) & log(x)
• Thus: \(log(Y) = B_0 + B(logX)\)
• And to convert from log into meaningful values:
• \(Y = e^{B_0 + B(logX)}\)
• Lets look at the log-log scatterplot

scatterplot(log(Sweating)~log(Anxiety), data= Power.Data)

• Looks like a line now!
• Let’s look at the model fit

Model.Sweat.LL<-lm(log(Sweating)~log(Anxiety), data= Power.Data)

	Dependent variable:
	log(Sweating)
	Log-Log Transform
Constant	-4.046*** (0.008)
log(Anxiety)	1.698*** (0.005)
Observations	250
R2	0.998
Adjusted R2	0.998
Residual Std. Error	0.046 (df = 248)
F Statistic	100,505.500*** (df = 1; 248)
Note:	p<0.1; p<0.05; p<0.01

Plot the fit and tell the package that you did a transform

plot(effect("Anxiety", Model.Sweat.LL,
           transformation=list(link=log, inverse=exp)))

Check the residuals

autoplot(Model.Sweat.LL, which = 1:2, label.size = 1) + theme_bw()

They look OK.

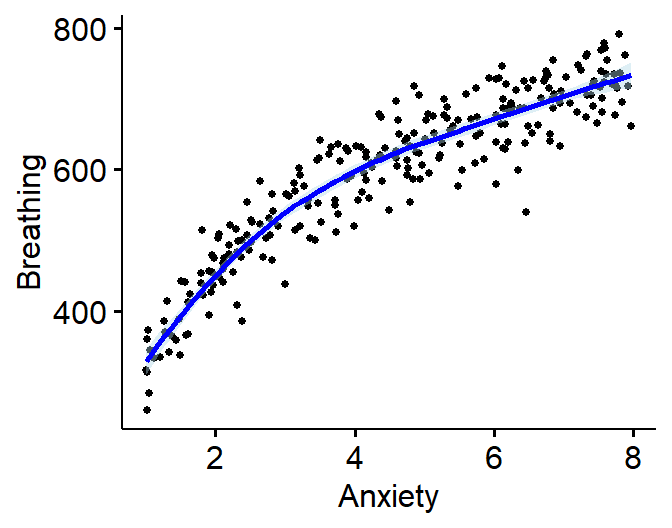
Logarithmic

• These functions are often physical (sound intensity, earthquakes, etc.)
• \(c^Y = dX\)
• Breathing rate (in ms between breaths) predicted by anxiety level
• Logarithmic Example: \(Y = .05(X*\epsilon)^{3.8}\)

set.seed(42)
n <- 250
x <- runif(n, 0, 7)+1
y <-200*log(x*(5+rnorm(n, sd=1)))
Logarithmic.Data<-data.frame(Anxiety=x,Breathing=y)

ggscatter(Logarithmic.Data, x = "Anxiety", y = "Breathing",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

• Plot Breathing by log(Anxiety)

scatterplot(Breathing~log(Anxiety), data= Logarithmic.Data)

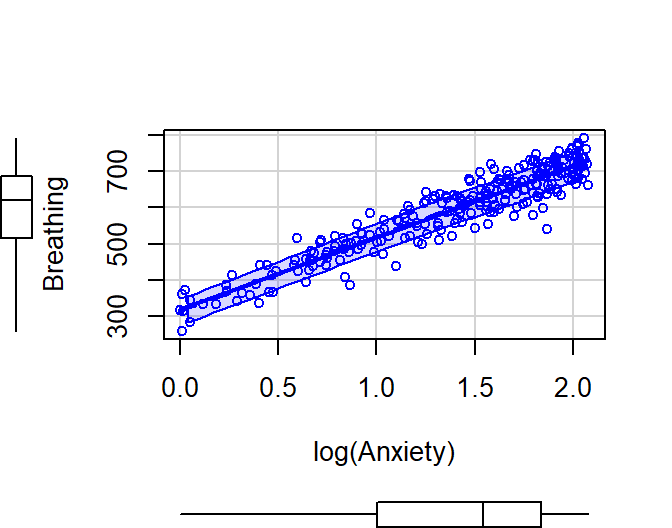
• Looks like a line now
• Let’s look at the model fit

Model.Breath.Log<-lm(Breathing~log(Anxiety), data= Logarithmic.Data)

	Dependent variable:
	Breathing
	Log Transform
Constant	319.641*** (6.656)
log(Anxiety)	197.847*** (4.456)
Observations	250
R2	0.888
Adjusted R2	0.888
Residual Std. Error	38.680 (df = 248)
F Statistic	1,971.251*** (df = 1; 248)
Note:	p<0.1; p<0.05; p<0.01

• Let’s plot the fit

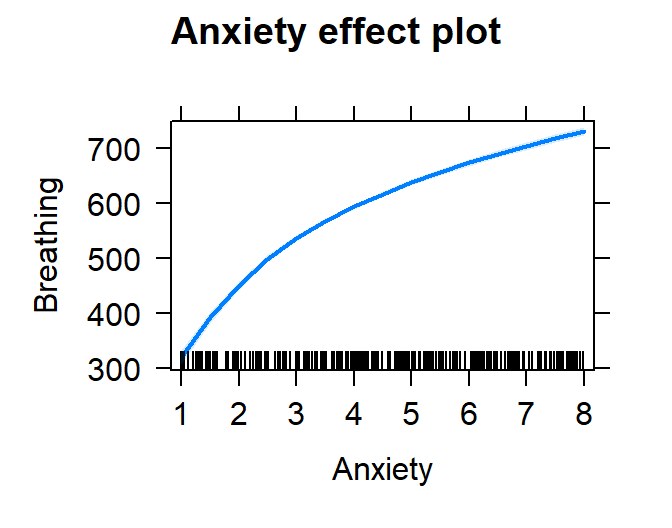
plot(effect("Anxiety", Model.Breath.Log))

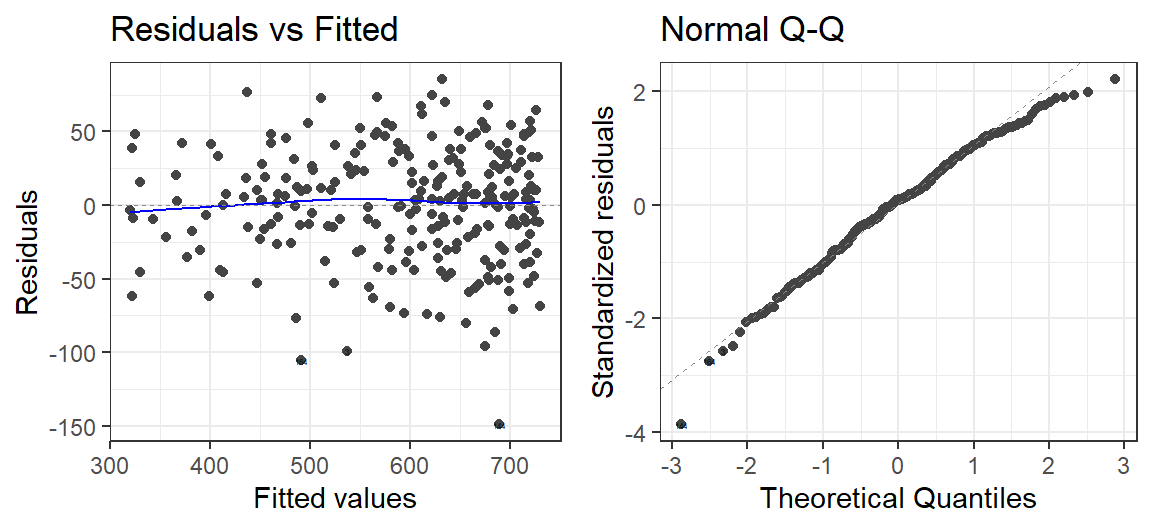
• Let’s check the residuals

autoplot(Model.Breath.Log, which = 1:2, label.size = 1) + theme_bw()

Reciprocals

• Common fix for rate data (things involving time)
• \(1/Y\)
• Adrenaline level in the blood predicted by mins after a panic attack (mins)
• Reciprocal Example: \(Y = (1/X)*\epsilon\)

set.seed(42)
n <- 250
# Length of panic attack
x <- 15*(runif(n, 1, 4))
y <- 1/(x)*rnorm(n,5,sd=.1)
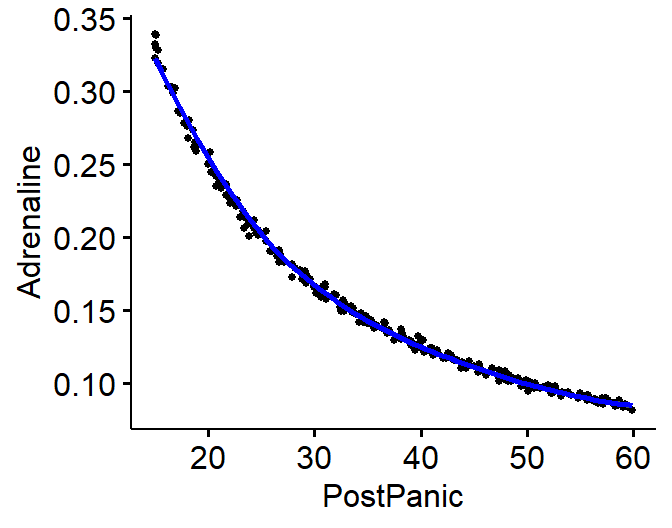
Reciprocal.Data<-data.frame(PostPanic=x,Adrenaline=y)

ggscatter(Reciprocal.Data, x = "PostPanic", y = "Adrenaline",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

We can take the Reciprocal of Adrenaline on the fly and replot

scatterplot(1/Adrenaline~PostPanic, data= Reciprocal.Data)

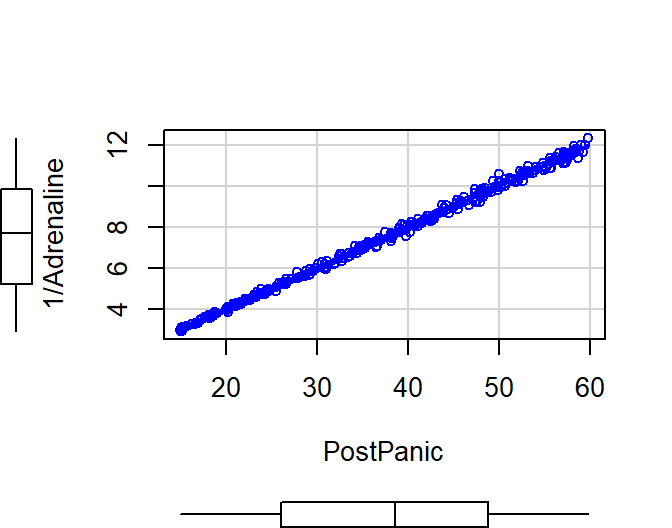
• Looks like a line now
• Let’s look at the model fit

Model.Calm.Rep<-lm(1/Adrenaline~PostPanic, data= Reciprocal.Data)

	Dependent variable:
	1/Adrenaline
Constant	-0.015 (0.029)
PostPanic	0.201*** (0.001)
Observations	250
R2	0.997
Adjusted R2	0.997
Residual Std. Error	0.149 (df = 248)
F Statistic	77,222.570*** (df = 1; 248)
Note:	p<0.1; p<0.05; p<0.01

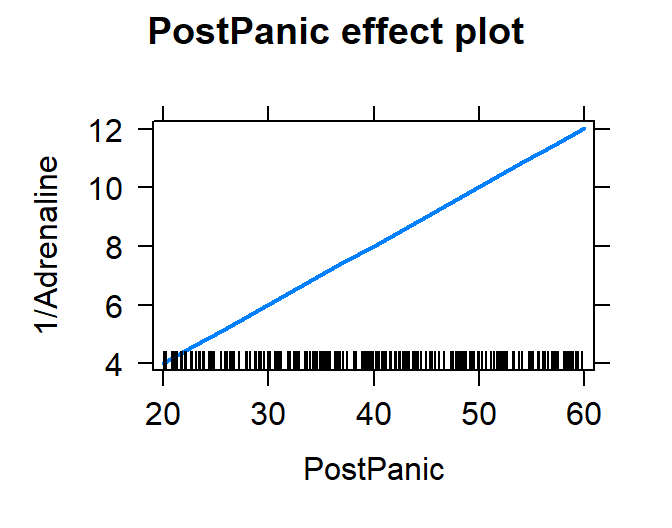
Plot the fit

plot(effect("PostPanic", Model.Calm.Rep))

Check the residuals

autoplot(Model.Calm.Rep, which = 1:2, label.size = 1) + theme_bw()

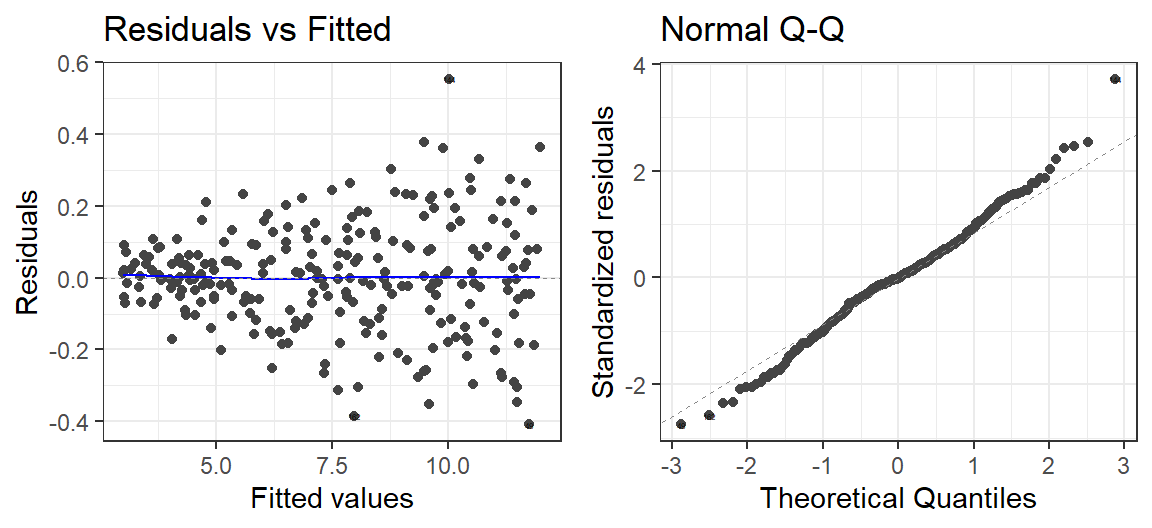
A little off (but I add in noise in a simple way)

Weird Bulges in the data (not full on curves)

• Data do not always fit our nice predefined functions
• Sometimes they clearly have bulges, but are we sure those are real?
• Bulges can be not real in small samples or can result from some latent factor you are not accounting for
• Let’s assume that if the data has a bulge that is real, meaningful, and we need to account for it
• We can use the Box-Cox Transform (fits different polynomials which we call \(\lambda\))
• \(Y = Y^\lambda - 1 / \lambda\), where \(\lambda \neq 0\) OR \(Y = lnY\), where \(\lambda = 0\)
• In this case, we will allow \(\lambda\) to be selected based on which makes the data most normal
• Let’s make a case with a weird power polynomial of 1.3 (something you would not notice in your raw data)

set.seed(42)
# 250 people
n <- 250
x <- runif(n, 0, 7)
y <- -4*x^1.3+ 20*x+rnorm(n, sd=2)+20
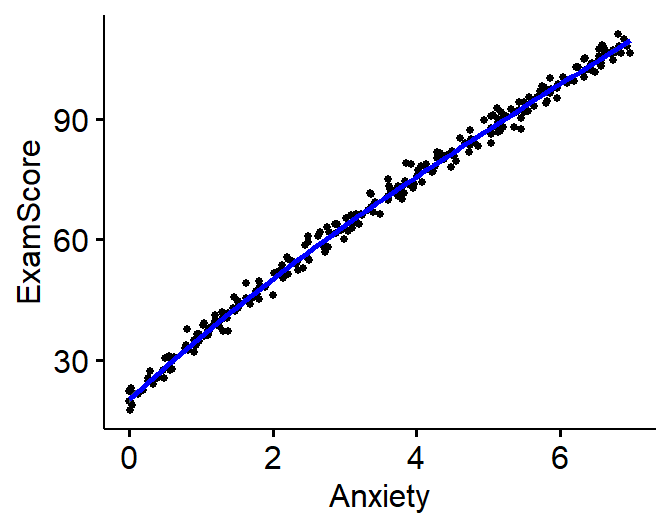
SortaQuad.Data<-data.frame(Anxiety=x,ExamScore=y)

ggscatter(SortaQuad.Data, x = "Anxiety", y = "ExamScore",
   add = "loess",  # Add loess
   add.params = list(color = "blue", fill = "lightblue"), # Customize reg. line
   conf.int = TRUE, # Add confidence interval
   cor.coef = FALSE, # Add correlation coefficient. see ?stat_cor
   size = 1 # Size of dots
   )

• Let’s try a linear model

Model.SortaQuad<-lm(ExamScore~Anxiety, data= SortaQuad.Data)

• Plot the Residuals

autoplot(Model.SortaQuad, which = 1:2, label.size = 1) + theme_bw()

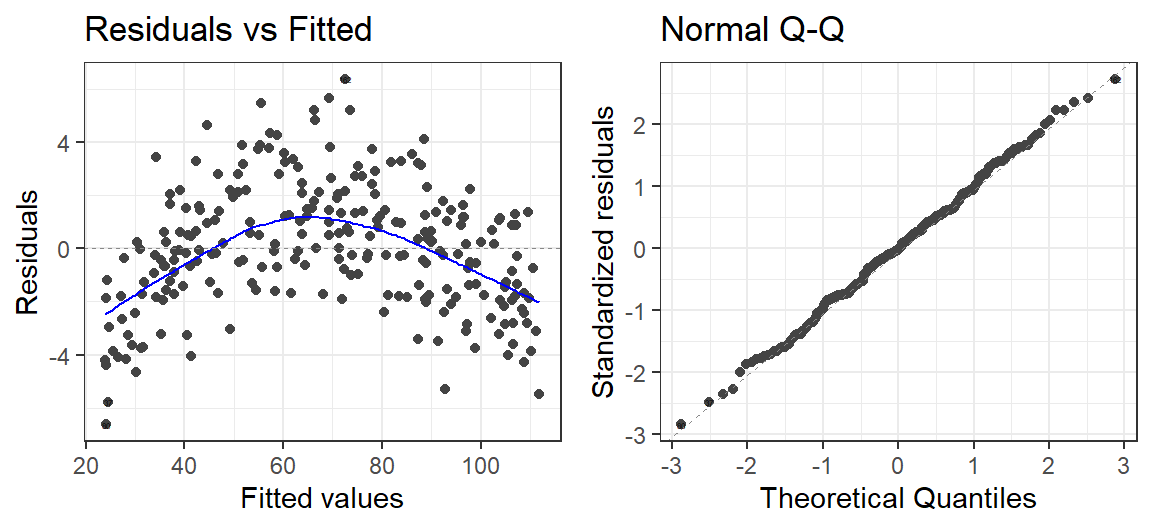
• It seems there is a slight curve in our data

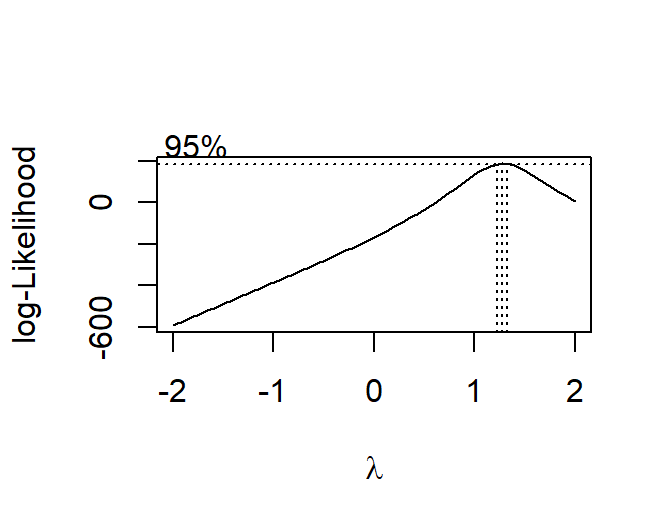
library(MASS)
bc<-boxcox(ExamScore ~Anxiety, data = SortaQuad.Data,
       lambda = seq(-2, 2, len = 20))
#we can extract the lambda
(lambda <- bc$x[which.max(bc$y)])

## [1] 1.272727

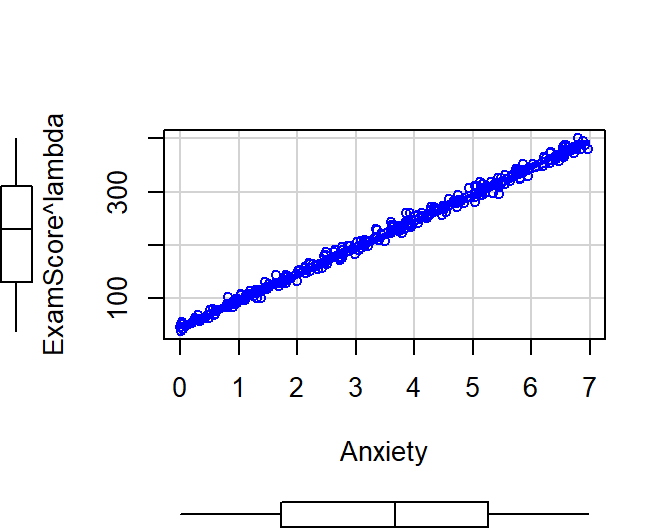
Plot the scatter and residuals from our transformed DV

scatterplot(ExamScore^lambda~Anxiety, data= SortaQuad.Data, reg.line=FALSE, smoother=loessLine)
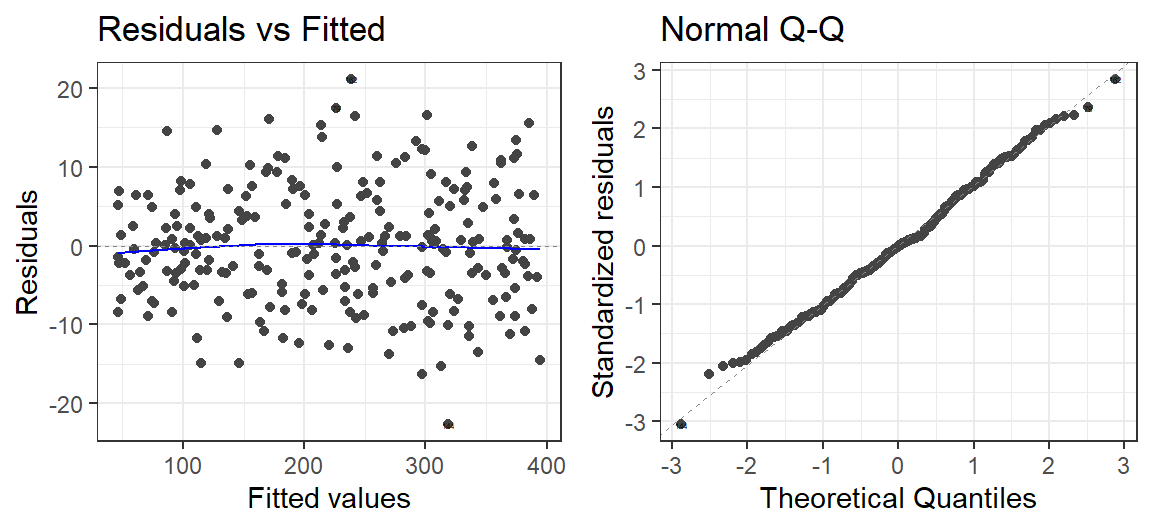
Model.SortaQuad.BC<-lm(ExamScore^lambda ~ Anxiety, data= SortaQuad.Data)

autoplot(Model.SortaQuad.BC, which = 1:2, label.size = 1) + theme_bw()

Some issues

• Box-Cox is a guess and requires some fine tuning (like adjusting the range of lambdas)
• You have to keep track of your zeros in the DV (so you can add constants to fix it)
• Most importantly, you have to make it harder to make sense of the DV (but your fits will be far better using it)