Moderated Mediation

Quick Review

Moderation (Process model 1)

“The moderator function of third variables, which partitions a focal independent variable into subgroups that establish its domains of maximal effectiveness regarding a given dependent variable” - Baron & Kenny, 1986.

For example, is success on a kindergarten entrance exam predicted by time to eat the marshmallow, but moderated by parenting style?

• Permissive parents (no boundaries) vs Authoritative (strict).
  • Measurement scale from -3 to 3 (permissive to authoritative)

Moderation

Steps

Center

Marshmallow.Mod$Parents.C<-scale(Marshmallow.Mod$Parents,scale=F)[,]
Marshmallow.Mod$Time.C<-scale(Marshmallow.Mod$Time,scale=F)[,]

Regression models

Mod.1<-lm(Success~Time.C+Parents.C, data= Marshmallow.Mod)
Mod.2<-lm(Success~Time.C*Parents.C, data= Marshmallow.Mod)

Test simple slopes

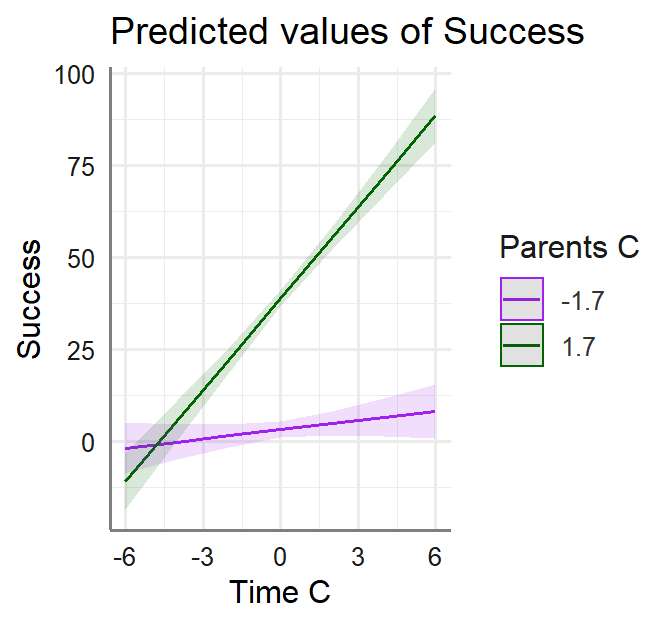
• Plot the results of each moderator to help us visualize the results
• We must set our moderator levels (-1SD [Permissive] and +1SD [Authoritative])

Permissive<--sd(Marshmallow.Mod$Parents.C)
Authoritative<-+sd(Marshmallow.Mod$Parents.C)

• Permissive: Parents.C = -1.7 score
• Authoritative: Parents.C = 1.7 score

- To do this quickly we will use rockchalk package, but to do this by hand you have to recenter the data (which we covered a few weeks ago).

library(rockchalk)
m1ps <- plotSlopes(Mod.2, modx = "Parents.C", plotx = "Time.C", n=2, modxVals="std.dev")
m1psts <- testSlopes(m1ps)
knitr::kable(round(m1psts$hypotests,4))

## Values of Parents.C OUTSIDE this interval:
##        lo        hi 
## -2.793686 -1.583800 
## cause the slope of (b1 + b2*Parents.C)Time.C to be statistically significant

	“Parents.C”	slope	Std. Error	t value	Pr(>|t|)
(m-sd)	-1.7	0.8331	0.5734	1.4530	0.1473
(m+sd)	1.7	8.2879	0.6062	13.6712	0.0000

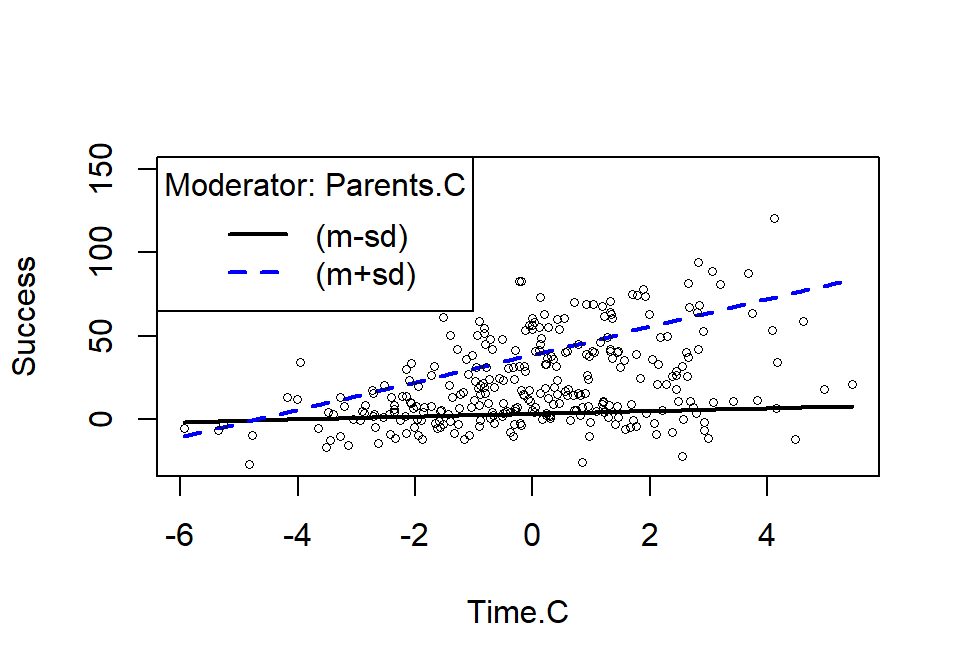
Summary

So what do these results tell us?

Review Mediation (Process Model 4)

“The mediator function of a third variable, which represents the generative mechanism through which the focal independent variable can influence the dependent variable of interest” - Baron & Kenny, 1986.

For example, do does children respect/trust in of authority figures to keep their promises intermediating in the causal chain for success.

Mediation

Test mediation

Steps, 1) Y~X [c path], 2) Med~X [a path], 3) Y~X+Med [b & c’ path]

library(mediation)
Model.2<-lm(Trust~Time, data= Marshmallow.Mod)
Model.3<-lm(Success~Trust+Time, data= Marshmallow.Mod)
Med.Boot.BCa <- mediate(Model.2, Model.3, boot = TRUE, 
                        boot.ci.type = "bca", sims=200, treat="Time", mediator="Trust")
summary(Med.Boot.BCa)

## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the BCa Method
## 
##                Estimate 95% CI Lower 95% CI Upper p-value    
## ACME              5.423        4.260         7.07  <2e-16 ***
## ADE              -0.363       -1.123         0.36    0.35    
## Total Effect      5.060        3.692         6.45  <2e-16 ***
## Prop. Mediated    1.072        0.949         1.27  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 300 
## 
## 
## Simulations: 200

Summary

So what do these results tell us?

Moderated-Mediated

“…moderated mediation occurs when the strength of an indirect effect depends on the level of some variable, or in other words, when mediation relations are contingent on the level of a moderator” - see Preacher, Rucker, & Hayes (2007)

• Moderation examines how subgroups influence the strength of the relationship between X to Y
• Mediation is trying to figure out the intermediating factors involved in getting from X to Y
  • Moderated-Mediated is that effect of the mediator is moderated

Example

You collect 300 4-year-olds, give them the Marshmallow test (measure their time to eat the marshmallow). You operationalize success as how they did at the end of the year on kindergarten entrance exam. - You also measure how must trust they have in authority figures (proposed Mediator). - You also measure the parenting style of the high warmth parents (proposed Moderator) - Permissive parents (no boundaries) vs Authoritative (strict) - Measurement scale from -3 to 3 (permissive to authoritative) - What if trust is moderated by parenting styles - We expect mediator (trust) to be stronger for kids with authoritative than permissive parents (indirect path) - But it could also be possible that children from authoritative parents who last longer will show more success (direct path)

Model approaches

There are multiple ways to think what about testing a moderated mediation. Preacher, Rucker, & Hayes (2007) argue you can test the moderation on a, b, c’ pathways directly and that should be theorized moderation based on where you theorize it to be. Imai et al, (2010) have proposed a different framework that allows for generalized approach, but they instead of think about it moderating the direct and indirect path (not a or b)

Only the indirect pathway is moderated

Both a and b path are moderated

Process Model 58

Just a path is moderated

Process Model 7

Just b path is moderated

Process Model 14

Direct and indirect pathway are moderated

Process59

Process8

Process15

Analysis

Simulation below:

Moderation on Path a, b, c’

• In this case, we think the direct (c’) and indirect path (a,b) is moderated by Parenting style. (Note this is Hayes’ process model 59)

Moderated Mediation

• So we have to interact it in Model 2 (Mediator Model) and Model 3 (Outcome Model)

• Model 2 from Kenny becomes, \(M ~ X*Mod\)

• Model 3 from Kenny becomes, \(Y ~ M*Mod+X*Mod\)

• Since we are going to be dealing with interactions, we should center our scores before analysis

• Center:

Marshmallow.Mod$Parents.C<-scale(Marshmallow.Mod$Parents,scale=F)[,]
Marshmallow.Mod$Time.C<-scale(Marshmallow.Mod$Time,scale=F)[,]
Marshmallow.Mod$Trust.C<-scale(Marshmallow.Mod$Trust,scale=F)[,]

• Regression models:

ModMed.Mediator<-lm(Trust~Parents.C*Time.C, data= Marshmallow.Mod)
ModMed.Outcome<-lm(Success~Trust.C*Parents.C+Time.C*Parents.C, data= Marshmallow.Mod)

• Mediator and Outcome Models (Note difference in DV when reading table):

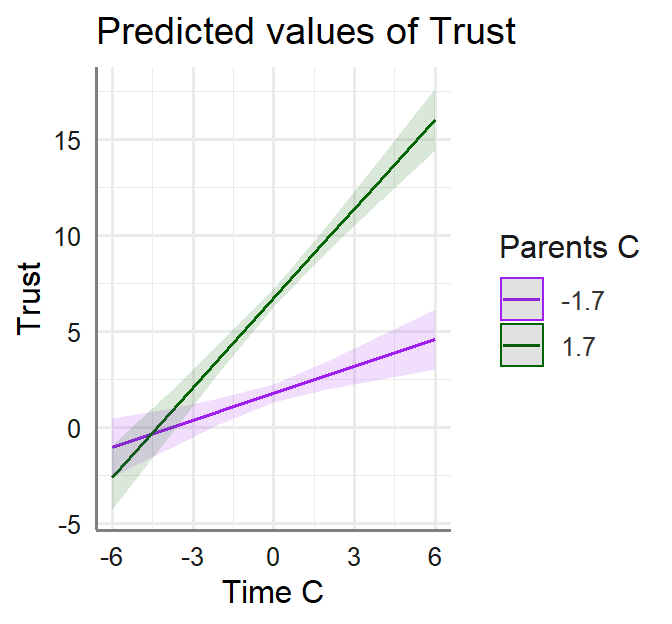
• Plot the results of each moderator to help us visualize the results
• We must set our moderator levels (-1SD [Permissive] and +1SD [Authoritative])

Permissive<--sd(Marshmallow.Mod$Parents.C)
Authoritative<-+sd(Marshmallow.Mod$Parents.C)

• Permissive: Parents.C = -1.7 score
• Authoritative: Parents.C = 1.7 score

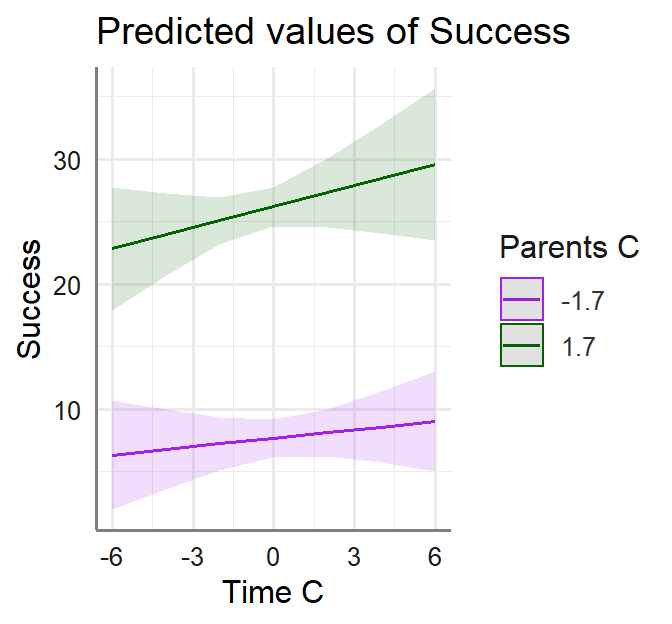
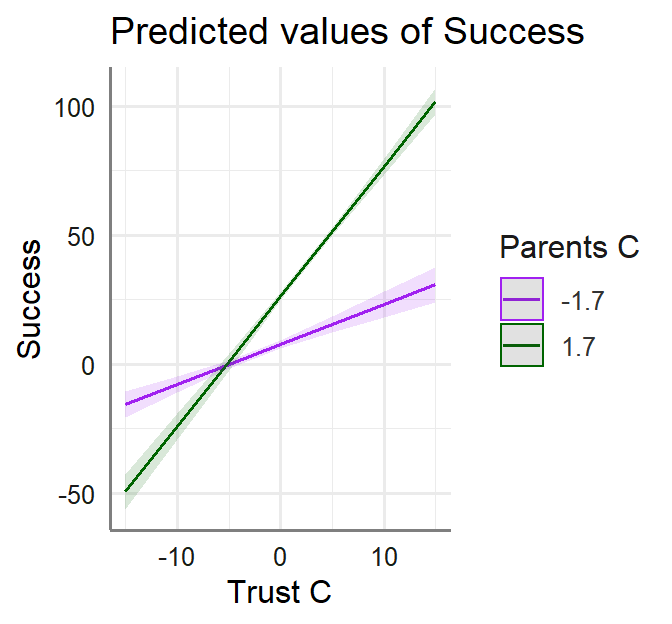
Test Moderation on Path a, b, c’

• In this mediation package we list the moderator as a covariate and set the levels we wish to test
  • Again, we can use the +/- 1SD from the mean (also we can use zero if wanted to see the average parent)
  • This allows us to view the impact of the moderator on the direct and indirect effect

Permissive Parents

• We set the covariates = list(Parents.C = Permissive) in our mediation (remember we defined this above as having a Parents.C = -1.7 score)

library(mediation)
ModMed.Boot.BCa.1 <- mediate(ModMed.Mediator, ModMed.Outcome, 
                              covariates = list(Parents.C = Permissive), boot = TRUE, 
                              boot.ci.type = "bca", sims=200, treat="Time.C", mediator="Trust.C")
summary(ModMed.Boot.BCa.1)
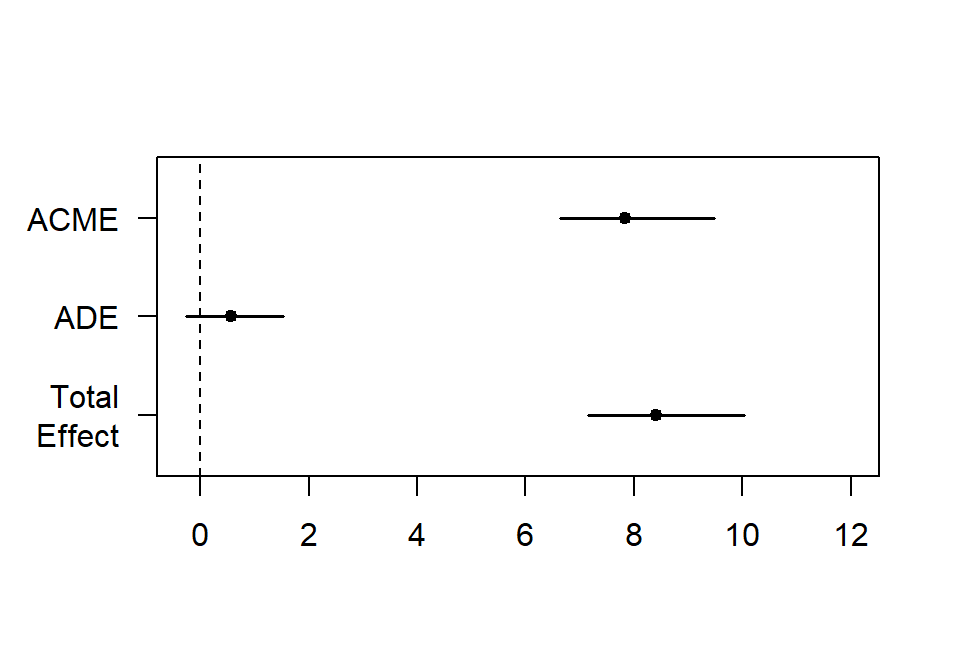
plot(ModMed.Boot.BCa.1)

## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the BCa Method
## 
## (Inference Conditional on the Covariate Values Specified in `covariates')
## 
##                Estimate 95% CI Lower 95% CI Upper p-value    
## ACME              0.726        0.406         1.23  <2e-16 ***
## ADE               0.221       -0.451         0.92    0.54    
## Total Effect      0.947        0.233         1.80  <2e-16 ***
## Prop. Mediated    0.767        1.715       222.99  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 300 
## 
## 
## Simulations: 200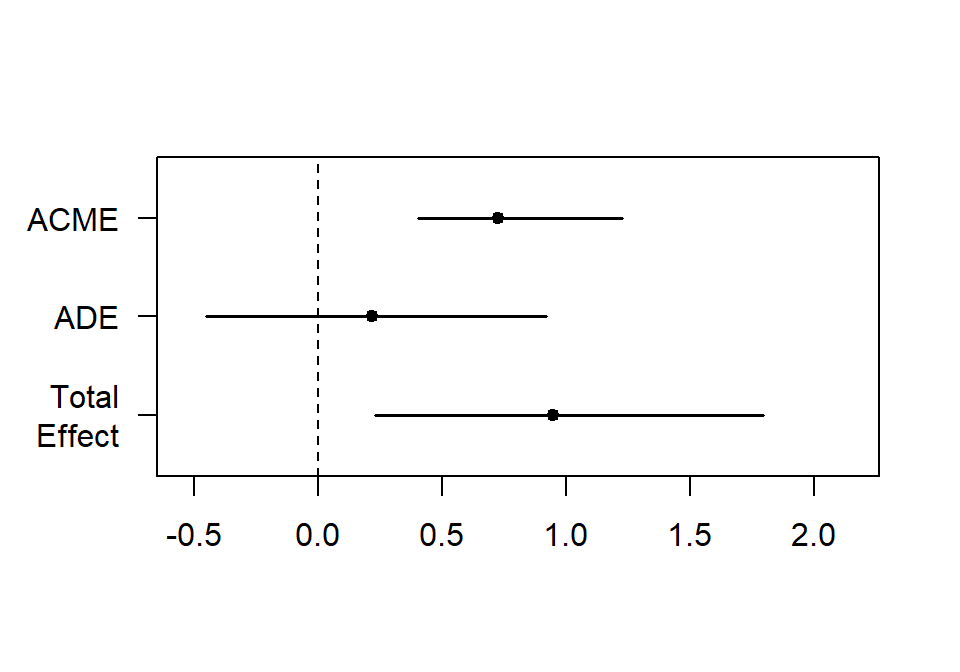

• No direct effect permissive parents, but there is an indirect effect:
  • For children of permissive parents, they are more successful if they have more trust

Authoritative Parents

• We set the covariates = list(Parents.C = Authoritative) in our mediation (remember we defined this above as having a Parents.C = 1.7 score)

ModMed.Boot.BCa.2 <- mediate(ModMed.Mediator, ModMed.Outcome, 
                              covariates = list(Parents.C = Authoritative), boot = TRUE, 
                              boot.ci.type = "bca", sims=200, treat="Time.C", mediator="Trust.C")
summary(ModMed.Boot.BCa.2)
plot(ModMed.Boot.BCa.2)

## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the BCa Method
## 
## (Inference Conditional on the Covariate Values Specified in `covariates')
## 
##                Estimate 95% CI Lower 95% CI Upper p-value    
## ACME              7.843        6.633         9.49  <2e-16 ***
## ADE               0.561       -0.257         1.53    0.14    
## Total Effect      8.404        7.152        10.02  <2e-16 ***
## Prop. Mediated    0.933        0.834         1.03  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 300 
## 
## 
## Simulations: 200

• No direct effect authoritative parents, but there is an indirect effect:
  • For children of authoritative parents, they are more successful if they have more trust

Difference Direct/indirect effect

• To get a significance test on if the moderator is causing a difference in the direct or indirect effects
  • 1. we must first run a third moderation (not accoutining for the covariate)
  • 2. use the test.modmed function at testing between the covariates, covariates.1 = list(Parents.C = Permissive) and covariates.2 = list(Parents.C = Authoritative)

ModMed.Boot.BCa.3 <- mediate(ModMed.Mediator, ModMed.Outcome, boot = TRUE, 
                              boot.ci.type = "bca", sims=200, treat="Time.C", mediator="Trust.C")
TestDiff<-test.modmed(ModMed.Boot.BCa.3, covariates.1 = list(Parents.C = Permissive),
            covariates.2 = list(Parents.C = Authoritative), sims = 200)
TestDiff

## 
##  Test of ACME(covariates.1) - ACME(covariates.2) = 0
## 
## data:  estimates from ModMed.Boot.BCa.3
## ACME(covariates.1) - ACME(covariates.2) = -7.1161, p-value < 2.2e-16
## alternative hypothesis: true ACME(covariates.1) - ACME(covariates.2) is not equal to 0
## 95 percent confidence interval:
##  -8.626936 -5.740560
## 
## 
##  Test of ADE(covariates.1) - ADE(covariates.2) = 0
## 
## data:  estimates from ModMed.Boot.BCa.3
## ADE(covariates.1) - ADE(covariates.2) = -0.34042, p-value = 0.61
## alternative hypothesis: true ADE(covariates.1) - ADE(covariates.2) is not equal to 0
## 95 percent confidence interval:
##  -1.6115384  0.7199354

• Given the we did not have a direct effect to begin with, the difference in direct effect levels is not interesting
• The difference in the indirect effect is significant (we have moderated mediation).
  • The negative value is that indirect effect for Permissive ACME) - Authoritative ACME = -7.12 and it was significantly different from 0. So the effect is bigger for Authoritative parenting as we predicted.

References

Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of personality and social psychology, 51(6), 1173.

Preacher, K. J., Rucker, D. D., & Hayes, A. F. (2007). Addressing moderated mediation hypotheses: Theory, methods, and prescriptions. Multivariate behavioral research, 42(1), 185-227.

Imai, K., Keele, L., & Tingley, D. (2010). A general approach to causal mediation analysis. Psychological methods, 15(4), 309.