Hierarchical-Linear Models

Multi-Level Models

• Hierarchical designs: Students nested in classrooms [Cluster] with student-level predictors
  • We will examine the effect of adding level 1 random slopes first today
• Multilevel designs: Students nested in classrooms with student-level and classroom-level predictors
  • Examine random slopes of level 2 variables (see http://www.alexanderdemos.org/Mixed3.html; We will not do this today)

Does clustering matter?

• You want to measure how students respond to a new type of active learning method (computer based) in math class
• You measure students math scores (DV) and the proportion of time (IV) they spend using the computer
  • You expect that the more time they spend doing the active learning method, the higher their math test scores will be
• You have access to different classrooms, but only 20 students per class (too small to publish)
  • So you decide to treat all students like they are from the same classroom

Simulation

• Set the same slope per class, but set a different intercept per class. Create 4 linear regressions and merge them.
• Note: You would not “know” that the slopes were the same and the intercepts differed.This is not how we would normally simulate this, but I have use this format to make match the simulations I have been showing you all semester.

#Set seed so your answers are all the same
set.seed(9)
# Sample Per class room people
n1 <- 20; n2 <- 20; n3 <- 20; n4 <- 20
N<-n1+n2+n3+n4 # Total N
# Uniform distrobution of proportion of time per classroom
X1 <- runif(n1,  0, .35)
X2 <- runif(n2, .3, .55)
X3 <- runif(n3, .5, .75)
X4 <- runif(n4, .7,1.0)
# noise per classroom
e1 <- rnorm(n1, 0, sd=2.5)
e2 <- rnorm(n2, 0, sd=2.5)
e3 <- rnorm(n3, 0, sd=2.5)
e4 <- rnorm(n4, 0, sd=2.5)
# Intercepts per classroom
B0.1 <- 80
B0.2 <- 70
B0.3 <- 60
B0.4 <- 50
# Same slope per classroom
B1=10
# Our equation to  create Y for each classroom
Y1 = B1*scale(X1,scale=F)  + B0.1 + e1
Y2 = B1*scale(X2,scale=F)  + B0.2 + e2
Y3 = B1*scale(X3,scale=F)  + B0.3 + e3
Y4 = B1*scale(X4,scale=F)  + B0.4 + e4
# Merge classrooms into 1 data.frame
Math.Data<-data.frame(Math=c(Y1,Y2,Y3,Y4),ActiveTime=c(X1,X2,X3,X4),
                      Classroom=c(rep("C1",n1),rep("C2",n2),rep("C3",n3),rep("C4",n4)),
                      StudentID=as.factor(1:N))

Step 1: Plot our results

• We will ignore classroom and simply plot the results
  • Note: *ggplot2 lets us plot the results with a regression line automatically added
    • ggplot2 works by adding “layers” to our data

library(ggplot2)
theme_set(theme_bw())
ClassRoom.Plot.1 <-ggplot(data = Math.Data, 
                          aes(x = ActiveTime, y=Math))+ #scaffold
  geom_point()+ # add layer of scatterplot
  geom_smooth(method = "lm", se = TRUE)+ # add regression line
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score") # add labels
ClassRoom.Plot.1 #call plot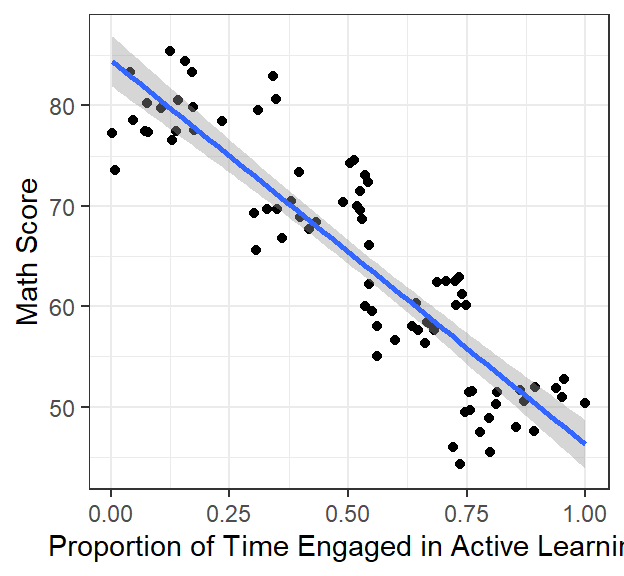

Step 2: Run Regression

• We will run the regression across all classrooms

library(stargazer)
Class.All<-lm(Math~ActiveTime, data = Math.Data)
stargazer(Class.All,type="latex",
          intercept.bottom = FALSE, single.row=TRUE, 
          star.cutoffs=c(.05,.01,.001), notes.append = FALSE,
          header=FALSE)

• Results show that a high intercept = 84.52 and a strong negative slope = -38.23 and a very high \(R^2\) = 0.8
• You expected a positive slope, but the graph shows a negative one (and so clearly at that!)
• With your massive \(R^2\) and counterintuitively strong negative slope you rush to publish in Psych Science and report, “Active learning is a flop! Dont waste your class time!”
  • Impact: Every math teacher in America changes their teaching, and the next generation of math students score worse than the last generation of student. You ruined America’s future. Good job!
  • What went wrong? Your \(R^2\) and slope were so huge you could not be possible wrong?!

What is Random?

• Each kid add noise (is a random effect)
• But are all the kids from all the classroom adding independent noise?
  • No! Students are not independent of each of other within the classroom
    • Error could be systematic (e.g., class clowns, class moral, room temp, time of day for the class) or unsystematic error, but that error that is unrelated to your main question
• Each classroom is, therefore a cluster where the kids scores are inter-related based their shared experience
  • The kids are nested in the classroom!
    • Another way to think about it: The kids are repeated measurements of their classroom

Re-examine by Cluster

• Hierarchical designs: Students nested in classrooms [Clustered] with student-level predictors Level 1

ClassRoom.Plot.2 <-ggplot(data = Math.Data, 
                          aes(x = ActiveTime, y=Math))+
  geom_point(aes(colour = Classroom, shape=Classroom))+ # we add color by cluster
  geom_smooth(method = "lm", se = TRUE)+
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score")+ # add labels
  theme(legend.position = "top")
ClassRoom.Plot.2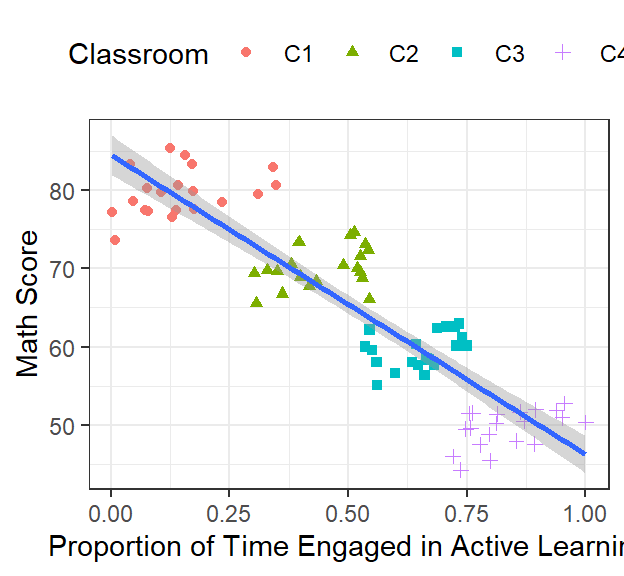

• Clearly there are difference between classrooms (Note: real data is never this well clustered)
• We can rerun the regression within each cluster to see the correct slopes.

ClassRoom.Plot <-ggplot(data = Math.Data, 
                        aes(x = ActiveTime, y=Math))+ 
  geom_point(aes(colour = Classroom, shape=Classroom))+
  geom_smooth(method = "lm", se = TRUE, aes(group = Classroom))+# we add group level
  xlab("Proportion of Time Engaged in Active Learning")+ylab("Math Score")+ # add labels
  theme(legend.position = "top")
ClassRoom.Plot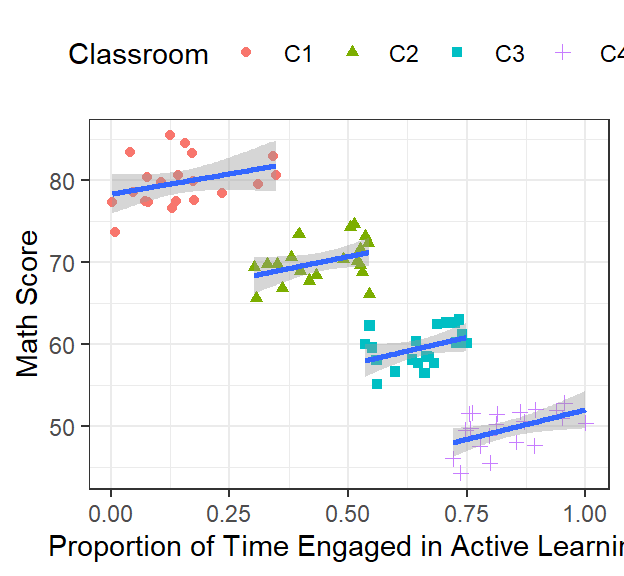

• The slopes look positive now!
• We need a regression method that capture the differences in the clusters and correctly estimate our slopes.

Hierarchical Linear Modeling

• We will focus today only 2 level model [students nested in classroom]

Levels

• Level 1 = Smallest level (often subjects/students)
• Level 2 = The group/cluster the students belong too (classrooms)
• You can have higher levels as well, such as Level 3 = Classrooms nested in schools

HLM with only Level 1 predictors

• Controlling for classroom differences, but making predictions about students

Equations (two level model)

• Quick review:

\[ Y_i = \beta_1X_1 +\beta_0 + \epsilon\]

Level 1

• Within each Group/Cluster (Students = \(i\) within Classroom 1 = \(j\), and we would replace \(j\) with \(g\) for Classroom 2 and so forth for each classroom!) \[y_{ij} = B_{1j}X_{ij} + B_{0j} + r_{ij} \]

• Where \(B_{0j}\) = intercept in group j

• Where \(B_{ij}\) = slope of students in group j

• Where \(r_{ij}\) = residuals of each i (student) within group j

Level 2

• Each Group/Cluster (Students = \(i\) within Classroom 1 = \(j\), Classroom 2 = \(g\), and so forth for each classroom)

Level 2 Intercept

\[B_{0j} = \gamma_{00}+u_{0j} \]

• Where \(\gamma_{00}\) = intercept of the classroom
• Where \(u_{0j}\) = random deviation of the classroom intercept from fixed population intercept
• We assume students will vary randomly around the population intercept of classroom

Level 2 Slope

\[B_{1j} = \gamma_{10}+u_{1j} \]

• Where \(\gamma_{10}\) = slope of the classroom
• Where \(u_{1j}\) = random deviation of the classroom slope from fixed population slope
• We assume students will vary randomly around the population intercept of classroom
• Note: We would repeat this for each level of classroom we have (g, etc)

Mixed Equation

• We put level 1 and level 2 together \[y_{ij} = (\gamma_{10}+u_{1j})X_{ij} + (\gamma_{00}+u_{0j})+ r_{ij} \]

Variance Components

• We now have multiple sources of error in our equation
• \(\sigma^2\) = variance of \(r_{ij}\), AKA variance due to error at level 1
• \(\tau_{00}\) = variance of \(u_{0j}\), AKA variance of random intercepts at level 2
• \(\tau_{11}\) = variance of \(u_{1j}\), AKA variance of random slopes at level 2
• \(\tau_{01}\) = co-variance of \(u_{0j}\) and \(u_{1j}\), AKA random slopes and random intercept can correlate

ICC

• The degree of clustering is measured via the inter-class correlation ICC

• The proportion of total variance that is between the groups \[ ICC = \frac{\tau}{\tau + \sigma^2}\]

• \(\tau\) = variance in a variable due to differences between a group

• \(\sigma^2\) = total variance across groups

• We would fit this on the null model (no level 1 predictors)

  • OLS regression assumes, ICC = 0: each classroom is unrelated to the others
  • If this value is large, it means that variance can be attributed to level 2

HLM analysis [Random Intecepts only Model]

• Linear regressions only has fixed-effects [continuous] or fixed-factors [groups]: variables of interest (often your manipulation)
  • The only random factor assumed is your subject’s response
• What if you have other effect or factors that might add random variation?
  • Random-effects/factors: Levels randomly sampled from a much larger population: Something you want to generalize across: Subjects, Classrooms, Words, Pictures, etc

LME4 package

• LME4 was created as a modern approach to mixed models.
• LME4 was designed specifically to be flexible in how we can control the random effect [Crossed & Nested] and how they correlated with other.
• What makes mixed useful (dealing with crossed and nested data) also makes it hard to get pvalues [which we will explore next week]

lmer function

• It is similar the lm function, but we add additional random effects
• lmer(DV ~ IV +(1|RandomFactor), data = X, REML= FALSE)
  • (1|RandomFactor), means let the intercept of the random factor vary a function of the group (cluster).
  • In our case, (1|Classroom), means that we let each classroom have its own intercept
  • REML = FALSE, means use a Maximum Likelihood estimation (not Restricted ML) [and of course not OLS]
  • Note: Kids were coded from 1 to total number of kids. We implicitly nested kids in that classrooms. Kid 1 is in classroom 1. Kids 21 is in classroom 2, etc.

Analysis

• Lets run our analysis first without centering the IVs.

Null Model

• No fixed factors (intercept only) with random intercept per classroom

library(lme4) 
Model.Null<-lmer(Math ~1+(1|Classroom),  
                   data=Math.Data, REML=FALSE)
summary(Model.Null)

## Linear mixed model fit by maximum likelihood  ['lmerMod']
## Formula: Math ~ 1 + (1 | Classroom)
##    Data: Math.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##    408.6    415.7   -201.3    402.6       77 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.34755 -0.72263  0.01011  0.73079  2.21975 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 126.884  11.264  
##  Residual                6.668   2.582  
## Number of obs: 80, groups:  Classroom, 4
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)    64.70       5.64   11.47

• Rule of thumb: t-values > |2| are significant
• Next we examine the intercepts for each classroom (random effect)

ranef(Model.Null)

## $Classroom
##    (Intercept)
## C1   14.959676
## C2    5.307215
## C3   -5.190059
## C4  -15.076832
## 
## with conditional variances for "Classroom"

• This is the difference from the grand mean
• Look at ICC: The var and sd of these values are what was seen in the table above
  • \(ICC = \frac{\tau}{\tau + \sigma^2}\), where \(\tau\) = 126.884 & \(\sigma^2\) = 6.668
  • use the function in r below from the sjstats package

sjstats::icc(Model.Null)

## # Intraclass Correlation Coefficient
## 
##     Adjusted ICC: 0.950
##   Unadjusted ICC: 0.950

• The ICC large and clearly > 0, meaning we were correct to think of this as HLM problem

Test Model

Model.1<-lmer(Math ~ActiveTime+(1|Classroom),  
                   data=Math.Data, REML=FALSE)
summary(Model.1)

## Linear mixed model fit by maximum likelihood  ['lmerMod']
## Formula: Math ~ ActiveTime + (1 | Classroom)
##    Data: Math.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##    399.3    408.8   -195.6    391.3       76 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.13111 -0.77650 -0.04481  0.61218  2.50097 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 200.00   14.142  
##  Residual                5.61    2.368  
## Number of obs: 80, groups:  Classroom, 4
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   58.862      7.261   8.107
## ActiveTime    11.269      3.140   3.589
## 
## Correlation of Fixed Effects:
##            (Intr)
## ActiveTime -0.224

• Lets sum it up.
  • Our intercept was 58.86, which was significant
  • Our slope was 11.27, which was significant (and positive)
  • Our random effects changed (now we added fixed effects)

What happened to \(R^2\)?

• To understand the \(R^2\) you need to first see the problem with predicting out random effects models

Plot the final model and \(R^2\) problems

• I find the effects package most accurate

library(effects)
Results.Model.1<-Effect(c("ActiveTime"),Model.1,
     xlevels=list(ActiveTime=seq(0,1,.2)))
     
Results.Model.1<-as.data.frame(Results.Model.1)

Final.Fixed.Plot.1 <-ggplot(data = Results.Model.1, 
                            aes(x = ActiveTime, y =fit))+
  geom_line(size=2)+
  coord_cartesian(xlim = c(0, 1),ylim = c(0, 100))+ 
  geom_ribbon(aes(ymin=fit-se, ymax=fit+se),alpha=.2)+
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score")+ 
  theme(legend.position = "none")
Final.Fixed.Plot.1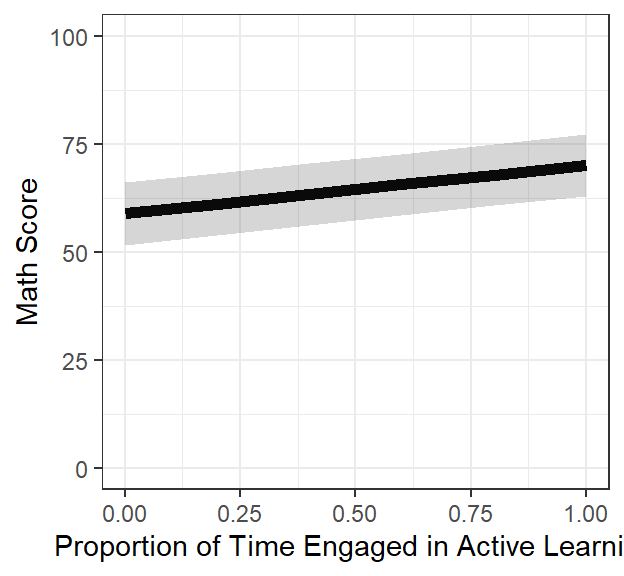

• Someone will ask you, “I want to see the real data”, meaning they want to see how the line fits the data.
• We plot the fixed effect on top of the raw data

#Fixed only, removed random effects
Math.Data$Model.1.Fitted<-predict(Model.1, re.form=NA)
     
ClassRoom.Plot.Bad <-ggplot(data = Math.Data)+ 
  coord_cartesian(xlim = c(0, 1),ylim = c(0, 100))+ 
  geom_point( aes(x = ActiveTime, y=Math, 
                                   colour = Classroom, shape=Classroom))+
  geom_line(aes(x = ActiveTime, y=Model.1.Fitted))+
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score")+ 
  theme(legend.position = "top")
ClassRoom.Plot.Bad

• Next, they will say, “Wow your model sucks and your \(R^2\) must be terrible. You suck as a modeler!”
• To test the \(R^2\) of the fixed effect of the final model over the raw data (meaning we IGNORE the random effects), all we have to do is run a linear regression of the fitted data fixed data to the raw data
• Nakagawa and Schielzeth (2013): function from https://github.com/jslefche/rsquared.glmm/blob/master/rsquaredglmm.R
  • \(R^2_{Marginal}\) = (fixed variance / Total variance)

\[ R^2_{Marginal} = \frac{\sigma^2_{fixed}} {\sigma^2_{fixed}+\sigma^2_{random}+\sigma^2_{residual}} \]

library(performance)
r2_nakagawa(Model.1)

## # R2 for Mixed Models
## 
##   Conditional R2: 0.974
##      Marginal R2: 0.044

• The Marginal \(R^2\) is terrible.

• Often you cannot simply add a scatterplot. However, there are ways around this (but you end up plotting every classroom)

• There is a fast and dirty method (but it will not work well when you have lots of control variables)

# Fixed + Random effects
Math.Data$Model.1.Fitted.Random<-predict(Model.1) 
     
ClassRoom.Plot.Better <-ggplot(data = Math.Data)+ 
  coord_cartesian(xlim = c(0, 1),ylim = c(0, 100))+ 
  geom_point(aes(x = ActiveTime, y=Math, 
                                   colour = Classroom, shape=Classroom))+
  geom_line(aes(x = ActiveTime, y=Model.1.Fitted.Random, 
                                  colour = Classroom))+
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Plot.Better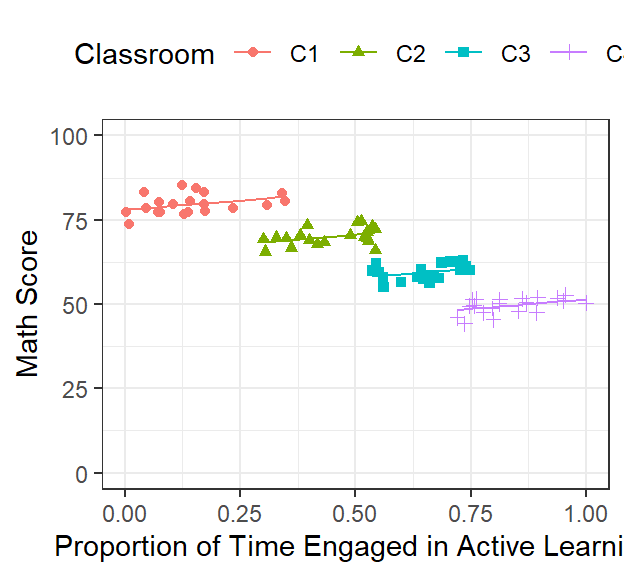

• This is what the model basically fit (controlling for the random effect)!

• a more accurate way to graph it is show the data in its clusters

ClassRoom.Plot.Best <-ggplot(data = Math.Data, group=Classroom)+ 
  facet_wrap(~Classroom)+
  coord_cartesian(xlim = c(0, 1),ylim = c(25, 100))+ 
  geom_point(aes(x = ActiveTime, y=Math, 
                                   colour = Classroom, shape=Classroom))+
  geom_line(aes(x = ActiveTime, y=Model.1.Fitted.Random))+
  xlab("Proportion of Time Engaged in Active Learning")+
  ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Plot.Best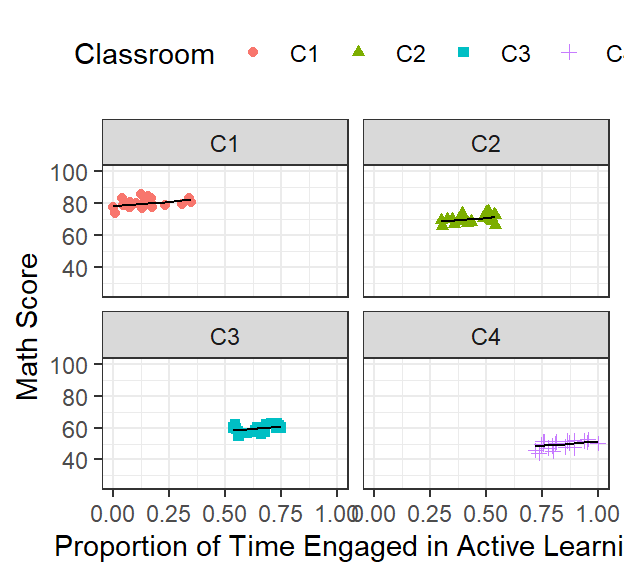

• The conditional \(R^2\) will be crazy high now (fixed variance + random variance/ Total variance)

\[ R^2_{conditional} = \frac{\sigma^2_{fixed}+\sigma^2_{random}} {\sigma^2_{fixed}+\sigma^2_{random}+\sigma^2_{residual}} \]

r2_nakagawa(Model.1)

## # R2 for Mixed Models
## 
##   Conditional R2: 0.974
##      Marginal R2: 0.044

\(R^2\)

• Both \(R^2\) values (fixed or fixed + random) don’t really have any meaning in the traditional sense
  • I showed you before with ICC how much of the variance was explained by the random effect
• Now I am just making it look like I fit all the data and I am the best modeler in the world.
  • In reality it is hard to really how good our fit is, so instead, we ask the question is the model with our predicts a better “fit” than our null or lower order model.

Deviance testing (-2 Log-Likelihood)

• We will cover the theory of this more next week
• For now just look at the pvalue (is model 1 better than the null model)

anova(Model.Null,Model.1)

## Data: Math.Data
## Models:
## Model.Null: Math ~ 1 + (1 | Classroom)
## Model.1: Math ~ ActiveTime + (1 | Classroom)
##            npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## Model.Null    3 408.59 415.74 -201.30   402.59                         
## Model.1       4 399.27 408.80 -195.64   391.27 11.321  1  0.0007662 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Centering

• I have not yet shown you how to center the IV correctly
• There are two approaches: Grand mean vs Group centering
  • When to center at the grand mean or the group?
    • This depends on your question and the data

Grand mean

• You may want to ask a grand mean question (how all people are impacted by the predictor regardless of group), but the data may not allow that question to be asked (if the predictor is confounded with group)
  • For example, in our example its dangerous to make predictions as ActiveTime range is confounded with classroom!
    • Remember be careful about making predictions about data you do not have

Math.Data$ActiveTime.C<-scale(Math.Data$ActiveTime, center=TRUE, scale=FALSE)
Model.1.GM<-lmer(Math ~ActiveTime.C+(1|Classroom),  
                   data=Math.Data, REML=FALSE)
summary(Model.1.GM)

## Linear mixed model fit by maximum likelihood  ['lmerMod']
## Formula: Math ~ ActiveTime.C + (1 | Classroom)
##    Data: Math.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##    399.3    408.8   -195.6    391.3       76 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.13111 -0.77650 -0.04481  0.61218  2.50097 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 200.00   14.142  
##  Residual                5.61    2.368  
## Number of obs: 80, groups:  Classroom, 4
## 
## Fixed effects:
##              Estimate Std. Error t value
## (Intercept)    64.704      7.076   9.144
## ActiveTime.C   11.269      3.140   3.589
## 
## Correlation of Fixed Effects:
##             (Intr)
## ActiveTim.C 0.000

• You will notice the slope is the same as before, but intercept changed
• The intercept is now the mean of ActiveTime = 0.5183501
• Why? See below:

Math.Data$Model.1.Fitted.Random.GM<-predict(Model.1.GM) #plots fixed Random effects
     
ClassRoom.Plot.Better <-ggplot()+ 
  coord_cartesian(xlim = c(-.5,.5),ylim = c(0, 100))+ 
  geom_point(data = Math.Data, aes(x = ActiveTime.C, y=Math, 
                                   colour = Classroom, shape=Classroom))+
  geom_line(data = Math.Data, aes(x = ActiveTime.C, y=Model.1.Fitted.Random.GM, 
                                  colour = Classroom))+
  xlab("Proportion of Time Engaged in Active Learning\n(Grand Mean Centered)")+
  ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Plot.Better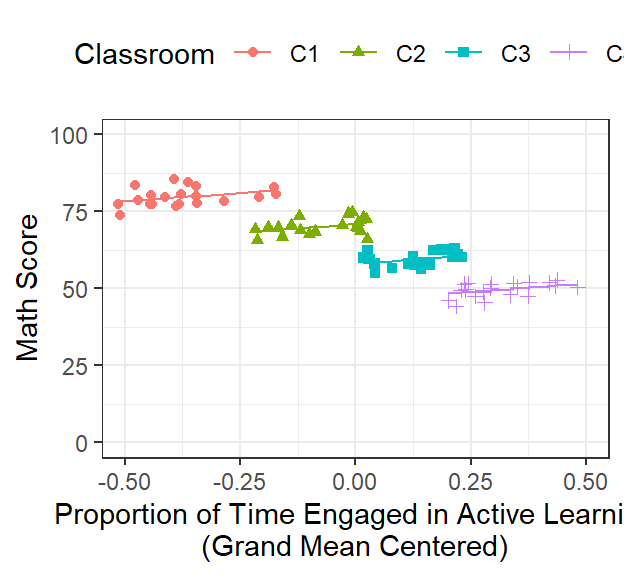

Group centering

• Group centering asks how does the within-group variation of the predictor predicts the outcome
  • This is often a very interesting question and may not always differ in story from the grand mean
• However, technically its meaning has changed!
  • So, you must think about what it means for your data to have centered within group

### Rescale IV
library(dplyr)
Math.Data<-Math.Data %>% 
  group_by(Classroom) %>% 
  mutate(ActiveTime.Class.Centered = ActiveTime - mean(ActiveTime))

• In this case our model will change a bit

Model.1.GC<-lmer(Math ~ActiveTime.Class.Centered+(1|Classroom),  
                   data=Math.Data, REML=FALSE)
summary(Model.1.GC)

## Linear mixed model fit by maximum likelihood  ['lmerMod']
## Formula: Math ~ ActiveTime.Class.Centered + (1 | Classroom)
##    Data: Math.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##    397.4    406.9   -194.7    389.4       76 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.16057 -0.78325 -0.04672  0.62451  2.50992 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 126.937  11.267  
##  Residual                5.606   2.368  
## Number of obs: 80, groups:  Classroom, 4
## 
## Fixed effects:
##                           Estimate Std. Error t value
## (Intercept)                 64.704      5.640  11.473
## ActiveTime.Class.Centered   11.990      3.159   3.795
## 
## Correlation of Fixed Effects:
##             (Intr)
## ActvTm.Cl.C 0.000

• The slope and intercept changed. Why? See below:

Math.Data$Model.1.Fitted.Random.GC<-predict(Model.1.GC) #plots fixed Random effects
     
ClassRoom.Plot.Better <-ggplot()+ 
  coord_cartesian(xlim = c(-.3,.3),ylim = c(0, 100))+ 
  geom_point(data = Math.Data, aes(x = ActiveTime.Class.Centered, y=Math, 
                                   colour = Classroom, shape=Classroom))+
  geom_line(data = Math.Data, aes(x = ActiveTime.Class.Centered, y=Model.1.Fitted.Random.GC, 
                                  colour = Classroom))+
  xlab("Proportion of Time Engaged in Active Learning\n(Centered per Classroom)")+
  ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Plot.Better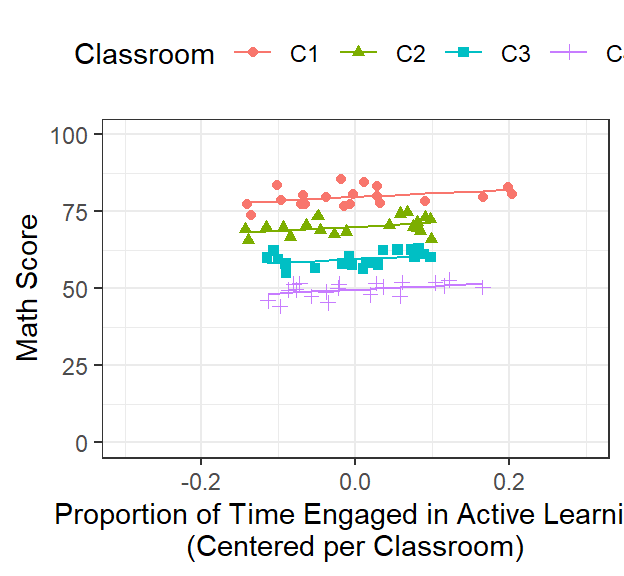

• Make sure to pay attention to the x-axis!