Subjects & Items: Parsimonious Modeling

Maximal Modeling

• Last week we reviewed why Barr et al., 2013 proposed to reduce the type I error rate and increase the power using the maximal random structure: lmer(DV~ A*B + (1+A*B:Subjects) + (1+A*B:Items))
• However, we ran into convergence issue in practice and seemed like trial and error was needed to find the best random structure combination. Further, the more within-subject factors you have, the more complex you random structure become and harder it is to reduce.

Parsimonious Approach

Bates et al. (2015) [RePsychLing package] & Matuschek et al. (2017) provide a principled approach to finding the best random structure for your data. Bates et al. suggest the convergence issues are because the random effects are too complex for the actual data (and overparameterized non-convergent LMM are not interpretable). They provide the example of in a 2x2 within-subject design you will have [(2X2 subjects) + (2X2 items) + 1 / 2] = 10 random parameters. When you go to 2x2x2, we will get 36 random parameters. A warning sign that your model is overparameterized are high random correlations, \(r > [-.8 , .8]\).

They suggest conducting a PCA analysis of the random effects (of the maximal model) to determine how random components are really needed explaining and if we need all the parameters we are using (like in factor analysis we can examine a scree plot). Even if the maximal model converges does not mean we need all those random parameters. The benefit of pruning the random effects back allows us to protect our Type I error but increase our power (Matuschek et al., 2017).

Once we figure out the most complex structure the data can sustain, we can use model fit comparisons of nested models to find the best random effects.

Simulation

• We will simulate a full crossed study with 30 subjects and 10 items, but we will examine results were layers levels of random effects to see how parsimonious modeling works.

: Fully crossed: (1+C1*C2|Subject) + (1+C1*C2|Item) + (1|Subject:Item)

• we will ignore the (1|Subject:Item) for simplicity today
• Simulations generated in Excel File we reviewed at the start of class.
• 2 x 2 repeated measure with 10 items: Population Effect: \(Y = 4X_1-4X_2+4X_1X_2+10\)
• [Simulation results in Sim8.csv]
• Conditions are effects coded \((-.5, .5)\)
• Download Data

DataSim8<-read.csv("Mixed/Sim8.csv")
DataSim8$C1<-factor(DataSim8$Condition1)
DataSim8$C2<-as.factor(DataSim8$Condition2)
DataSim8$Item<-as.factor(DataSim8$Item)
DataSim8$Subject<-as.factor(DataSim8$Subject)

Simulation 1: No Random Slopes/Items

• Here we simulate population effects for our 2x2 design, but for each subject we simply add noise to each measurement \(Y = 4X_1-4X_2+4X_1X_2+10 + \epsilon\) . Thus there are No random slopes per subject, and there are no item level effects. In short, this is basically a plain old linear regression, and every measurement per subject is independent (an lm model would be fine with this data).

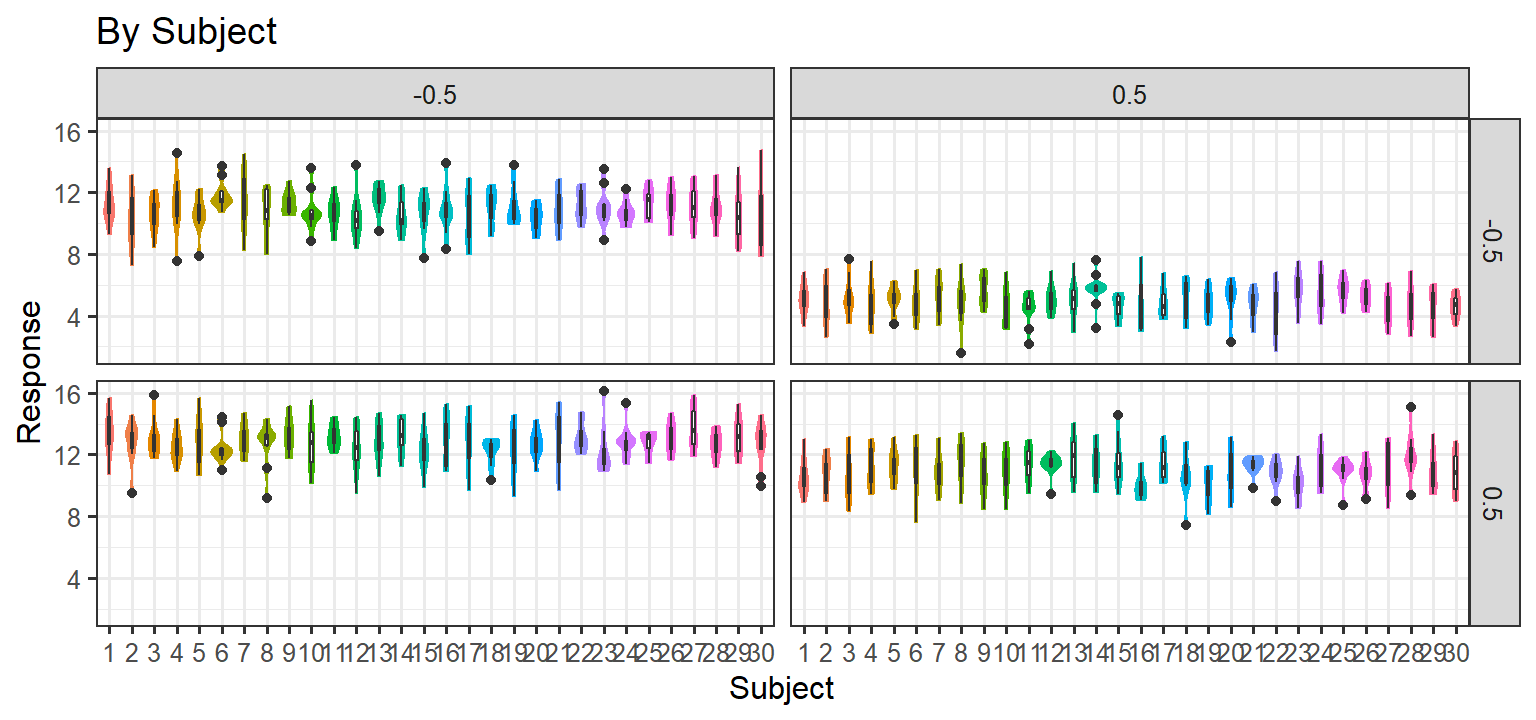
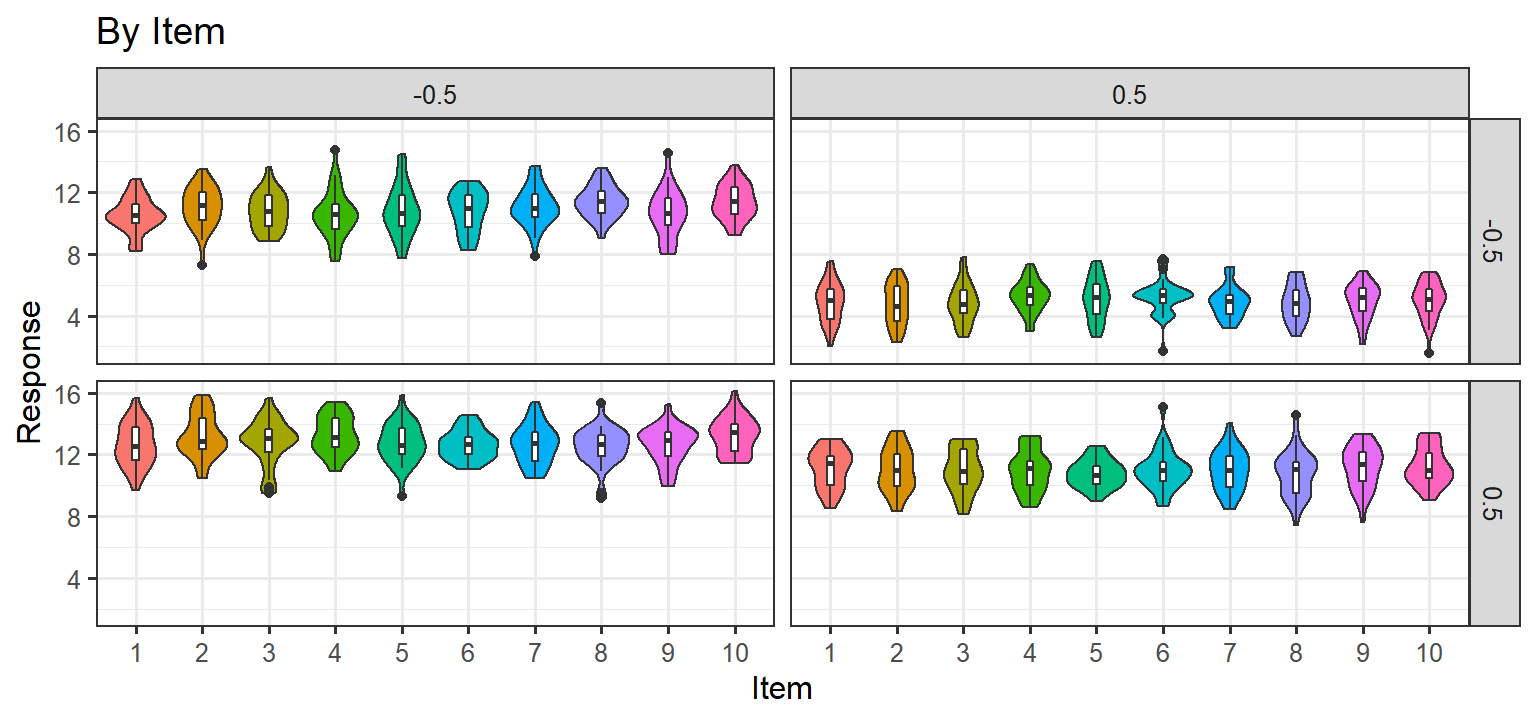
Parsimonious Stages

• Step 1: (1+C1*C2|Subject) + (1+C1*C2|Item)

library(lme4)
FullMax.SSNoise<-lmer(DV_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1*Condition2|Item),
              data=DataSim8, REML=FALSE)
summary(FullMax.SSNoise, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 |  
##     Subject) + (1 + Condition1 * Condition2 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4045.5   4172.7  -1997.7   3995.5     1175 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.95067 -0.66431  0.01886  0.66489  3.13739 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr             
##  Subject  (Intercept)           0.000212 0.01456                   
##           Condition1            0.059057 0.24302  1.00             
##           Condition2            0.006627 0.08141  1.00  1.00       
##           Condition1:Condition2 0.068101 0.26096  1.00  1.00  1.00 
##  Item     (Intercept)           0.004994 0.07066                   
##           Condition1            0.012173 0.11033   0.44            
##           Condition2            0.024671 0.15707  -0.83  0.13      
##           Condition1:Condition2 0.062291 0.24958  -0.09 -0.94 -0.47
##  Residual                       1.604201 1.26657                   
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            9.93133    0.04293 15.31430  231.32  < 2e-16 ***
## Condition1             3.97857    0.09238 18.67659   43.07  < 2e-16 ***
## Condition2            -3.88643    0.08964 13.92792  -43.36 2.93e-16 ***
## Condition1:Condition2  4.09045    0.17288 16.22527   23.66 5.24e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• The model failed to converge and problems with our correlations and zero intercepts
• Step 2: extract the PCA of the random structure from the maximal model

library(RePsychLing)
FullMax.SSNoise.PCA<-rePCA(FullMax.SSNoise)
summary(FullMax.SSNoise.PCA)

## $Subject
## Importance of components:
##                         [,1]      [,2]      [,3]      [,4]
## Standard deviation     0.289 0.0007822 5.401e-05 3.246e-06
## Proportion of Variance 1.000 0.0000100 0.000e+00 0.000e+00
## Cumulative Proportion  1.000 1.0000000 1.000e+00 1.000e+00
## 
## $Item
## Importance of components:
##                          [,1]   [,2]      [,3]      [,4]
## Standard deviation     0.2221 0.1247 4.451e-05 1.171e-05
## Proportion of Variance 0.7603 0.2397 0.000e+00 0.000e+00
## Cumulative Proportion  0.7603 1.0000 1.000e+00 1.000e+00

• For Subject: we see the first component captures 100% of the random variance.
• For Item: we see the first two components capture 100% of the random variance.
• Step 3: Reduce complexity Cycle:

Cycle 1

• The random correlations are showing problems, lets remove them.

FullMax.SSNoise.2<-lmer(DV_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2||Subject)
              +(1+Condition1*Condition2||Item),
              data=DataSim8, REML=FALSE)
summary(FullMax.SSNoise.2, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## DV_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 ||  
##     Subject) + (1 + Condition1 * Condition2 || Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4026.2   4092.4  -2000.1   4000.2     1187 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.93808 -0.67371  0.01669  0.64739  3.14696 
## 
## Random effects:
##  Groups    Name                  Variance  Std.Dev. 
##  Subject   (Intercept)           0.000e+00 0.000e+00
##  Subject.1 Condition1            4.845e-02 2.201e-01
##  Subject.2 Condition2            7.051e-10 2.655e-05
##  Subject.3 Condition1:Condition2 9.043e-10 3.007e-05
##  Item      (Intercept)           2.898e-04 1.702e-02
##  Item.1    Condition1            0.000e+00 0.000e+00
##  Item.2    Condition2            8.432e-03 9.182e-02
##  Item.3    Condition1:Condition2 2.042e-03 4.519e-02
##  Residual                        1.629e+00 1.276e+00
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)            9.93133    0.03723 10.00456  266.76  < 2e-16 ***
## Condition1             3.97857    0.08392 29.99973   47.41  < 2e-16 ***
## Condition2            -3.88643    0.07919  9.99973  -49.08 2.98e-13 ***
## Condition1:Condition2  4.09045    0.14805  9.97458   27.63 9.34e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Recheck the PCA

FullMax.SSNoise.PCA2<-rePCA(FullMax.SSNoise.2)
summary(FullMax.SSNoise.PCA2)

## $Subject
## Importance of components:
##                          [,1]      [,2]      [,3] [,4]
## Standard deviation     0.1725 2.356e-05 2.081e-05    0
## Proportion of Variance 1.0000 0.000e+00 0.000e+00    0
## Cumulative Proportion  1.0000 1.000e+00 1.000e+00    1
## 
## $Item
## Importance of components:
##                           [,1]    [,2]    [,3] [,4]
## Standard deviation     0.07195 0.03541 0.01334    0
## Proportion of Variance 0.78338 0.18970 0.02692    0
## Cumulative Proportion  0.78338 0.97308 1.00000    1

• Model is still overparameterized.

Cycle 2

• Remove the zero random effect

FullMax.SSNoise.3<-lmer(DV_SSNoise ~ Condition1*Condition2
              +(1+Condition1||Subject)
              +(1+Condition2||Item),
              data=DataSim8, REML=FALSE)
summary(FullMax.SSNoise.3, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 || Subject) +  
##     (1 + Condition2 || Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4018.2   4064.0  -2000.1   4000.2     1191 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.93921 -0.67450  0.01678  0.64702  3.14649 
## 
## Random effects:
##  Groups    Name        Variance  Std.Dev.
##  Subject   (Intercept) 0.0000000 0.00000 
##  Subject.1 Condition1  0.0484452 0.22010 
##  Item      (Intercept) 0.0002885 0.01698 
##  Item.1    Condition2  0.0084285 0.09181 
##  Residual              1.6286530 1.27619 
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                         Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)              9.93133    0.03723   10.00135  266.76  < 2e-16 ***
## Condition1               3.97857    0.08393   30.00000   47.41  < 2e-16 ***
## Condition2              -3.88643    0.07919   10.00007  -49.08 2.98e-13 ***
## Condition1:Condition2    4.09045    0.14736 1150.00164   27.76  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Recheck the PCA

FullMax.SSNoise.PCA3<-rePCA(FullMax.SSNoise.3)
summary(FullMax.SSNoise.PCA3)

## $Subject
## Importance of components:
##                          [,1] [,2]
## Standard deviation     0.1725    0
## Proportion of Variance 1.0000    0
## Cumulative Proportion  1.0000    1
## 
## $Item
## Importance of components:
##                           [,1]    [,2]
## Standard deviation     0.07194 0.01331
## Proportion of Variance 0.96691 0.03309
## Cumulative Proportion  0.96691 1.00000

• Model is still way overparameterized.

Cycle 3

• Clear we don’t need the random slope on the subject.
• Given that random slope on items captures .03% of the variance we may not need it.

FullMax.SSNoise.4<-lmer(DV_SSNoise ~ Condition1*Condition2
              +(1|Subject)
              +(1|Item),
              data=DataSim8, REML=FALSE)
summary(FullMax.SSNoise.4, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SSNoise ~ Condition1 * Condition2 + (1 | Subject) + (1 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4015.4   4051.0  -2000.7   4001.4     1193 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.8825 -0.6529  0.0059  0.6545  3.1948 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev.
##  Subject  (Intercept) 0.0000000 0.00000 
##  Item     (Intercept) 0.0001682 0.01297 
##  Residual             1.6429917 1.28179 
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                         Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)              9.93133    0.03723    9.97956  266.76   <2e-16 ***
## Condition1               3.97857    0.07400 1189.97847   53.76   <2e-16 ***
## Condition2              -3.88643    0.07400 1189.97847  -52.52   <2e-16 ***
## Condition1:Condition2    4.09045    0.14801 1189.97847   27.64   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Check fit

## Data: DataSim8
## Models:
## FullMax.SSNoise.4: DV_SSNoise ~ Condition1 * Condition2 + (1 | Subject) + (1 | Item)
## FullMax.SSNoise.3: DV_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 || Subject) + (1 + Condition2 || Item)
##                   npar    AIC  BIC  logLik deviance Chisq Df Pr(>Chisq)
## FullMax.SSNoise.4    7 4015.4 4051 -2000.7   4001.4                    
## FullMax.SSNoise.3    9 4018.2 4064 -2000.1   4000.2 1.175  2     0.5557

Results of Simulation 1

Random Intercepts model is as good a fit as that last overparameterized model. As would expect, there are no random slopes or item level effects (LMM is not needed, but the process told us that pretty clearly)

Simulation 2: Random Slopes per subject + Noise/No Item level effect

• Here we let each subject have their own slope for each condition (1 & 2) and the interaction. We also add noise to each trial, but items have no random effect. Thus there are ARE random slopes per subject, and there are no item level effects. If this approach matches the data, we will be left with this random structure: (1+C1*C2|Subject) + (1|Item)

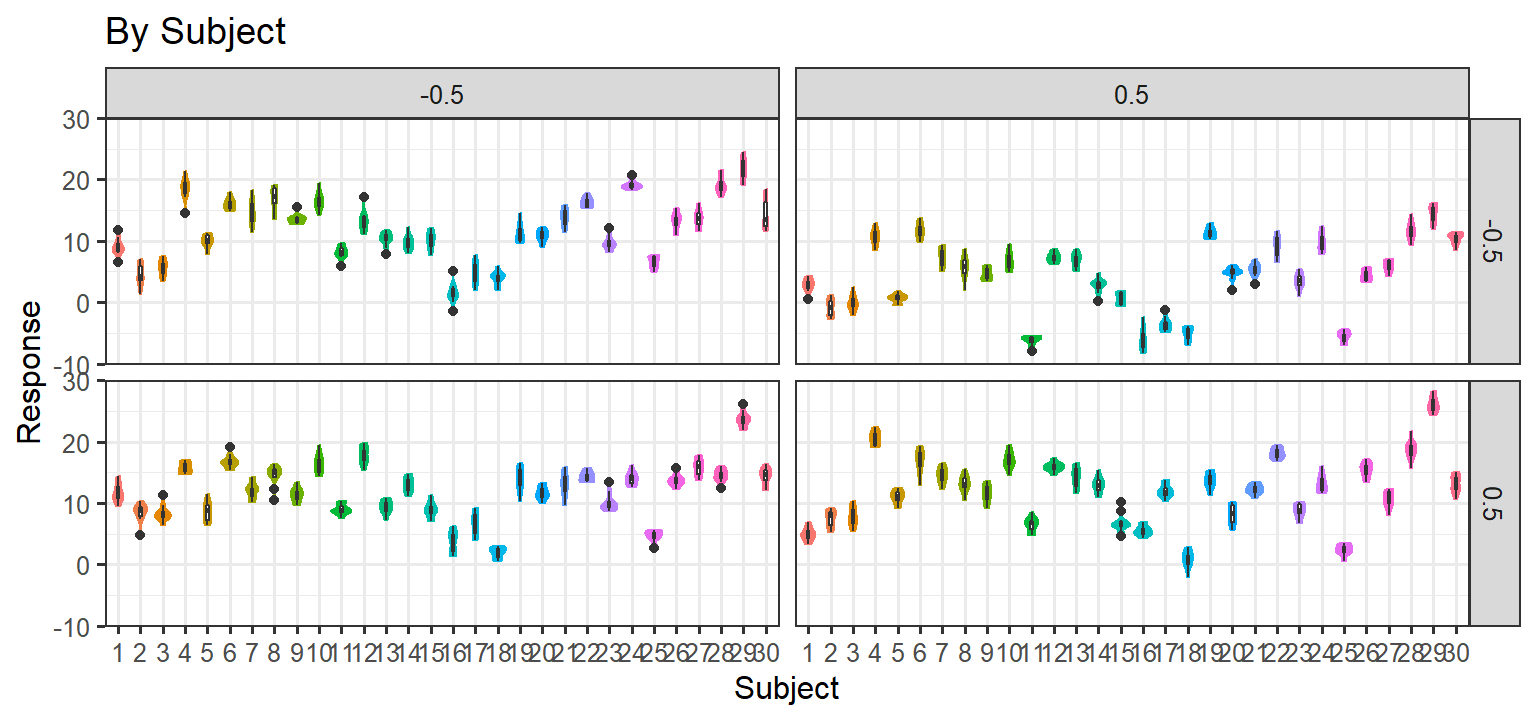
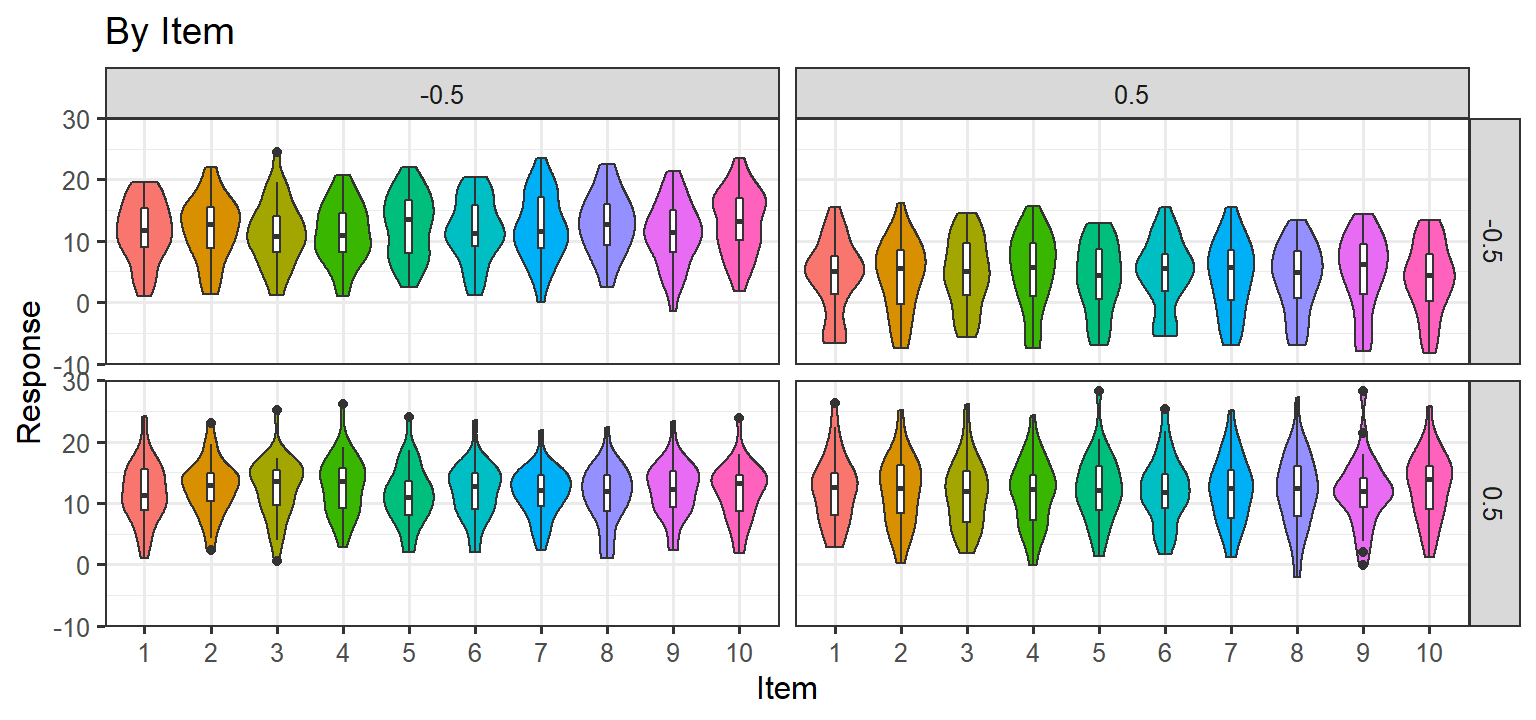
Parsimonious Stages

• Step 1: (1+C1*C2|Subject) + (1+C1*C2|Item)

DV_SS_RSlope_SSNoise.M1<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1*Condition2|Item),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M1, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 + Condition1 * Condition2 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4539.2   4666.4  -2244.6   4489.2     1175 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.8240 -0.6370  0.0118  0.6150  3.7034 
## 
## Random effects:
##  Groups   Name                  Variance  Std.Dev. Corr             
##  Subject  (Intercept)           23.436815 4.84116                   
##           Condition1             4.416334 2.10151  -0.20            
##           Condition2             4.036480 2.00910   0.39  0.08      
##           Condition1:Condition2 13.515658 3.67636   0.03  0.27  0.05
##  Item     (Intercept)            0.006239 0.07898                   
##           Condition1             0.022577 0.15026   0.15            
##           Condition2             0.029861 0.17280  -0.93  0.23      
##           Condition1:Condition2  2.707920 1.64558   0.39 -0.85 -0.71
##  Residual                        1.624477 1.27455                   
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.0711     0.8850 30.0546  11.380 2.03e-12 ***
## Condition1              3.8278     0.3936 30.7373   9.726 6.77e-11 ***
## Condition2             -3.7412     0.3781 31.0274  -9.895 4.08e-11 ***
## Condition1:Condition2   7.5843     0.8620 33.4311   8.799 3.22e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• The model fit and everything seems to be OK, but random correlations on the items are bit high.
• Step 2: extract the PCA of the random structure from the maximal model

DV_SS_RSlope_SSNoise.M1.PCA<-rePCA(DV_SS_RSlope_SSNoise.M1)
summary(DV_SS_RSlope_SSNoise.M1.PCA)

## $Subject
## Importance of components:
##                          [,1]   [,2]    [,3]    [,4]
## Standard deviation     3.8711 2.9343 1.61133 1.32623
## Proportion of Variance 0.5361 0.3080 0.09289 0.06293
## Cumulative Proportion  0.5361 0.8442 0.93707 1.00000
## 
## $Item
## Importance of components:
##                          [,1]    [,2]      [,3]     [,4]
## Standard deviation     1.2988 0.12740 0.0001189 3.64e-20
## Proportion of Variance 0.9905 0.00953 0.0000000 0.00e+00
## Cumulative Proportion  0.9905 1.00000 1.0000000 1.00e+00

• For Subject: we see all components capture some random variance, but the last term is rather a small amount. Maybe we don’t need the interaction (we will check this later)?

• For Item: we see the first two components capture 100% of the random variance. So we really don’t need all that complexity.

• Step 3: Reduce complexity Cycle

Cycle 1

• Keep Subjects the same for now, but remove the random slopes per subject as 99% of the variance was captured by the random intercepts

DV_SS_RSlope_SSNoise.M2<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1*Condition2||Item),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M2, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 + Condition1 * Condition2 || Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4534.5   4631.2  -2248.2   4496.5     1181 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7800 -0.6295  0.0127  0.6215  3.5679 
## 
## Random effects:
##  Groups   Name                  Variance  Std.Dev. Corr             
##  Subject  (Intercept)           23.432281 4.84069                   
##           Condition1             4.410880 2.10021  -0.20            
##           Condition2             4.034431 2.00859   0.39  0.08      
##           Condition1:Condition2 13.508926 3.67545   0.03  0.27  0.05
##  Item     (Intercept)            0.001747 0.04179                   
##  Item.1   Condition1             0.000000 0.00000                   
##  Item.2   Condition2             0.014630 0.12095                   
##  Item.3   Condition1:Condition2  2.708513 1.64576                   
##  Residual                        1.639378 1.28038                   
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.0711     0.8847 30.0274  11.384 2.03e-12 ***
## Condition1              3.8278     0.3905 30.0135   9.802 7.24e-11 ***
## Condition2             -3.7412     0.3760 30.3695  -9.949 4.52e-11 ***
## Condition1:Condition2   7.5843     0.8620 33.3288   8.799 3.31e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Recheck the PCA

DV_SS_RSlope_SSNoise.M2.PCA<-rePCA(DV_SS_RSlope_SSNoise.M2)
summary(DV_SS_RSlope_SSNoise.M2.PCA)

## $Subject
## Importance of components:
##                          [,1]   [,2]    [,3]    [,4]
## Standard deviation     3.8530 2.9208 1.60211 1.31972
## Proportion of Variance 0.5362 0.3081 0.09271 0.06291
## Cumulative Proportion  0.5362 0.8444 0.93709 1.00000
## 
## $Item
## Importance of components:
##                         [,1]    [,2]    [,3] [,4]
## Standard deviation     1.285 0.09447 0.03264    0
## Proportion of Variance 0.994 0.00537 0.00064    0
## Cumulative Proportion  0.994 0.99936 1.00000    1

• Still overparameterized for random effect on items

Cycle 2

• Remove condtion 2 from items

DV_SS_RSlope_SSNoise.M3<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1||Item),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M3, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 + Condition1 || Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4617.4   4703.9  -2291.7   4583.4     1183 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9268 -0.6401  0.0307  0.6732  2.9642 
## 
## Random effects:
##  Groups   Name                  Variance  Std.Dev.  Corr             
##  Subject  (Intercept)           2.343e+01 4.840e+00                  
##           Condition1            4.394e+00 2.096e+00 -0.20            
##           Condition2            4.015e+00 2.004e+00  0.39  0.08      
##           Condition1:Condition2 1.326e+01 3.642e+00  0.03  0.27  0.05
##  Item     (Intercept)           2.245e-04 1.498e-02                  
##  Item.1   Condition1            3.258e-09 5.708e-05                  
##  Residual                       1.822e+00 1.350e+00                  
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.0711     0.8846 30.0105   11.38 2.05e-12 ***
## Condition1              3.8278     0.3906 29.9989    9.80 7.30e-11 ***
## Condition2             -3.7412     0.3741 29.9974  -10.00 4.56e-11 ***
## Condition1:Condition2   7.5843     0.6829 30.0137   11.11 3.75e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Recheck the PCA

DV_SS_RSlope_SSNoise.M3.PCA<-rePCA(DV_SS_RSlope_SSNoise.M3)
summary(DV_SS_RSlope_SSNoise.M3.PCA)

## $Subject
## Importance of components:
##                          [,1]   [,2]    [,3]    [,4]
## Standard deviation     3.6544 2.7471 1.51483 1.24734
## Proportion of Variance 0.5395 0.3049 0.09271 0.06286
## Cumulative Proportion  0.5395 0.8444 0.93714 1.00000
## 
## $Item
## Importance of components:
##                          [,1]      [,2]
## Standard deviation     0.0111 4.229e-05
## Proportion of Variance 1.0000 1.000e-05
## Cumulative Proportion  1.0000 1.000e+00

• Model is still overparameterized for items

Cycle 3

• It seems we should only have intercepts only for items

DV_SS_RSlope_SSNoise.M4<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1|Item),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M4, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4615.4   4696.8  -2291.7   4583.4     1184 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9268 -0.6401  0.0307  0.6732  2.9642 
## 
## Random effects:
##  Groups   Name                  Variance  Std.Dev. Corr             
##  Subject  (Intercept)           2.343e+01 4.84031                   
##           Condition1            4.393e+00 2.09593  -0.20            
##           Condition2            4.016e+00 2.00398   0.39  0.08      
##           Condition1:Condition2 1.326e+01 3.64178   0.03  0.27  0.05
##  Item     (Intercept)           2.215e-04 0.01488                   
##  Residual                       1.822e+00 1.34992                   
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.0711     0.8846 30.0137  11.385 2.04e-12 ***
## Condition1              3.8278     0.3905 30.0100   9.802 7.25e-11 ***
## Condition2             -3.7412     0.3741 29.9897 -10.001 4.58e-11 ***
## Condition1:Condition2   7.5843     0.6829 30.0172  11.106 3.74e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00236296 (tol = 0.002, component 1)

• Check fit

## Data: DataSim8
## Models:
## DV_SS_RSlope_SSNoise.M4: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 | Subject) + (1 | Item)
## DV_SS_RSlope_SSNoise.M3: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 | Subject) + (1 + Condition1 || Item)
##                         npar    AIC    BIC  logLik deviance Chisq Df Pr(>Chisq)
## DV_SS_RSlope_SSNoise.M4   16 4615.4 4696.8 -2291.7   4583.4                    
## DV_SS_RSlope_SSNoise.M3   17 4617.4 4703.9 -2291.7   4583.4     0  1     0.9982

• Removing items did not hurt us

Cycle 4

• It seems we should remove the random interaction at subjects?

DV_SS_RSlope_SSNoise.M5<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1+Condition2|Subject)
              +(1|Item),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M5, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 +  
##     Condition2 | Subject) + (1 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4965.2   5026.2  -2470.6   4941.2     1188 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.86669 -0.66924  0.02599  0.64881  2.87445 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr       
##  Subject  (Intercept) 23.411   4.838               
##           Condition1   4.304   2.075    -0.20      
##           Condition2   3.925   1.981     0.39  0.09
##  Item     (Intercept)  0.000   0.000               
##  Residual              2.719   1.649               
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                        Estimate Std. Error        df t value Pr(>|t|)    
## (Intercept)             10.0711     0.8847   30.0032  11.384 2.05e-12 ***
## Condition1               3.8278     0.3905   30.0073   9.801 7.27e-11 ***
## Condition2              -3.7412     0.3740   30.0015 -10.002 4.55e-11 ***
## Condition1:Condition2    7.5843     0.1904 1109.9980  39.833  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Items is gone now as well, but removing the interaction hurt us?

• Check fit

## Data: DataSim8
## Models:
## DV_SS_RSlope_SSNoise.M5: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 + Condition2 | Subject) + (1 | Item)
## DV_SS_RSlope_SSNoise.M4: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 | Subject) + (1 | Item)
##                         npar    AIC    BIC  logLik deviance  Chisq Df
## DV_SS_RSlope_SSNoise.M5   12 4965.2 5026.2 -2470.6   4941.2          
## DV_SS_RSlope_SSNoise.M4   16 4615.4 4696.8 -2291.7   4583.4 357.76  4
##                         Pr(>Chisq)    
## DV_SS_RSlope_SSNoise.M5               
## DV_SS_RSlope_SSNoise.M4  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Model 4 was better, but let’s try one more simplification

DV_SS_RSlope_SSNoise.M6<-lmer(DV_SS_RSlope_SSNoise ~ Condition1*Condition2
              +(1+Condition1*Condition2||Subject),
              data=DataSim8, REML=FALSE)
summary(DV_SS_RSlope_SSNoise.M6, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 || Subject)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4610.5   4656.3  -2296.2   4592.5     1191 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.92704 -0.62995  0.03026  0.67443  2.97098 
## 
## Random effects:
##  Groups    Name                  Variance Std.Dev.
##  Subject   (Intercept)           23.435   4.841   
##  Subject.1 Condition1             4.394   2.096   
##  Subject.2 Condition2             4.015   2.004   
##  Subject.3 Condition1:Condition2 13.267   3.642   
##  Residual                         1.822   1.350   
## Number of obs: 1200, groups:  Subject, 30
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.0711     0.8847 30.0002  11.384 2.06e-12 ***
## Condition1              3.8278     0.3906 30.0000   9.801 7.30e-11 ***
## Condition2             -3.7412     0.3740 30.0001 -10.002 4.55e-11 ***
## Condition1:Condition2   7.5843     0.6830 30.0003  11.104 3.78e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Check fit

## Data: DataSim8
## Models:
## DV_SS_RSlope_SSNoise.M6: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 || Subject)
## DV_SS_RSlope_SSNoise.M4: DV_SS_RSlope_SSNoise ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 | Subject) + (1 | Item)
##                         npar    AIC    BIC  logLik deviance  Chisq Df
## DV_SS_RSlope_SSNoise.M6    9 4610.5 4656.3 -2296.2   4592.5          
## DV_SS_RSlope_SSNoise.M4   16 4615.4 4696.8 -2291.7   4583.4 9.0836  7
##                         Pr(>Chisq)
## DV_SS_RSlope_SSNoise.M6           
## DV_SS_RSlope_SSNoise.M4     0.2467

• Model 6 is basically as good as model 4

Results of Simulation 2

• Model 6 seems best which makes sense given how we simulated the data, and we have cut the random parameters down by 7. You will notice the t-values from models 4 and 6 are very similar. Those parameters were not doing much for us. Also, items did not do anything for us, but that is logical given they did not vary.

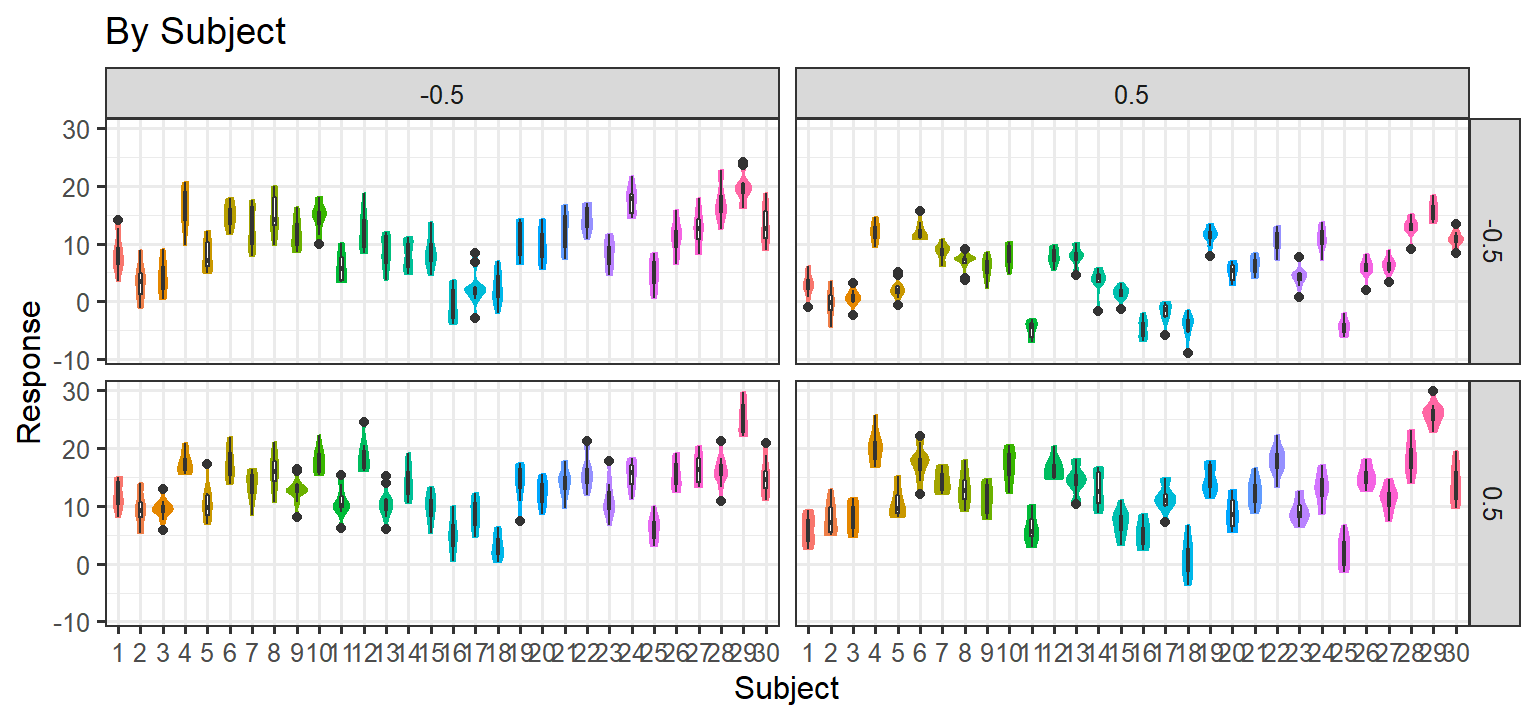
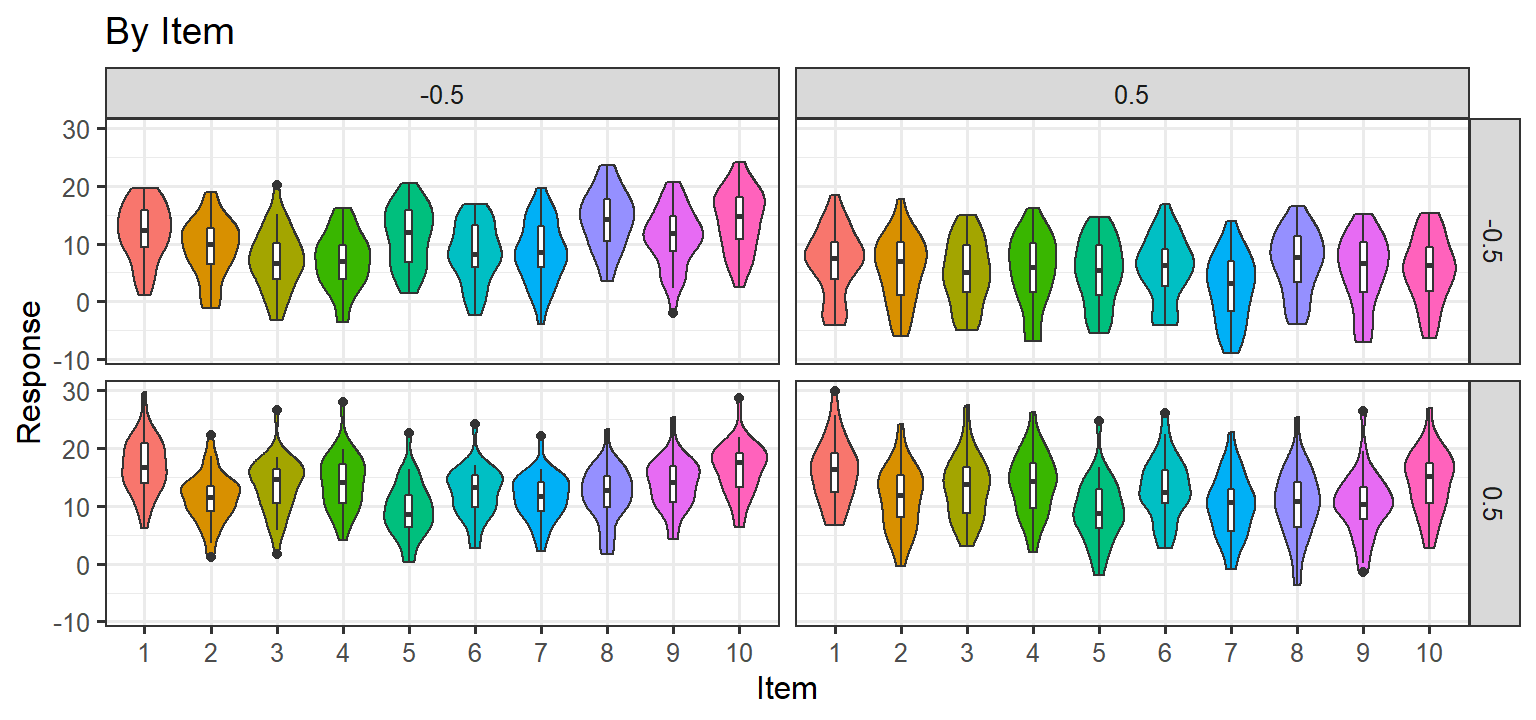
Simulation 3: Random Slopes per subject + Noise/Item level Random Effects

• Here we let each subject have their own slope for each condition (1 & 2) and the interaction. We also add noise to each trial, and each item has a random effect. Thus there are ARE random slopes per subject and per item. and there are no item level effects. If this approach matches the data, we will be left with this random structure: (1+C1*C2|Subject) + (1+C1*C2|Item)

Parsimonious Stages

• Step 1: (1+C1*C2|Subject) + (1+C1*C2|Item)

Max.M1<-lmer(DV_SS_RSlope_SSNoise_Items ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1*Condition2|Item),
              data=DataSim8, REML=FALSE)
summary(Max.M1, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## DV_SS_RSlope_SSNoise_Items ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 + Condition1 * Condition2 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4619.4   4746.6  -2284.7   4569.4     1175 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9978 -0.6342  0.0002  0.6443  3.5752 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr             
##  Subject  (Intercept)           23.551   4.853                     
##           Condition1             4.507   2.123    -0.20            
##           Condition2             4.096   2.024     0.38  0.09      
##           Condition1:Condition2  3.489   1.868     0.10  0.21  0.09
##  Item     (Intercept)            2.194   1.481                     
##           Condition1             5.177   2.275     0.25            
##           Condition2             2.256   1.502    -0.32  0.47      
##           Condition1:Condition2  2.599   1.612     0.23 -0.60 -0.69
##  Residual                        1.640   1.281                     
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.1912     1.0029 39.2576  10.162 1.50e-12 ***
## Condition1              4.7773     0.8206 16.0111   5.822 2.59e-05 ***
## Condition2             -2.9977     0.6063 22.2226  -4.944 5.87e-05 ***
## Condition1:Condition2   3.9174     0.6309 18.3156   6.209 6.81e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00415805 (tol = 0.002, component 1)

• The model fit and everything seems to be OK, but random correlations on the items are bit high.
• Step 2: extract the PCA of the random structure from the maximal model

Max.M1.PCA<-rePCA(Max.M1)
summary(Max.M1.PCA)

## $Subject
## Importance of components:
##                          [,1]   [,2]    [,3]    [,4]
## Standard deviation     3.8626 1.7788 1.40911 1.29085
## Proportion of Variance 0.6864 0.1456 0.09135 0.07666
## Cumulative Proportion  0.6864 0.8320 0.92334 1.00000
## 
## $Item
## Importance of components:
##                          [,1]   [,2]   [,3]    [,4]
## Standard deviation     2.1269 1.4167 0.7041 0.65489
## Proportion of Variance 0.6068 0.2692 0.0665 0.05752
## Cumulative Proportion  0.6068 0.8760 0.9425 1.00000

• For Subject & Item: we see all components capture some random variance.

• Step 3: Reduce complexity Cycle

Cycle 1

• The only thing I can try to simply is to remove the random correlations and see if it does not change the fit.
• Remove effects on items:

Max.M2<-lmer(DV_SS_RSlope_SSNoise_Items ~ Condition1*Condition2
              +(1+Condition1*Condition2|Subject)
              +(1+Condition1*Condition2||Item),
              data=DataSim8, REML=FALSE)
summary(Max.M2, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## DV_SS_RSlope_SSNoise_Items ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 | Subject) + (1 + Condition1 * Condition2 || Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4621.1   4717.8  -2291.5   4583.1     1181 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9004 -0.6446  0.0127  0.6317  3.5407 
## 
## Random effects:
##  Groups   Name                  Variance Std.Dev. Corr             
##  Subject  (Intercept)           23.608   4.859                     
##           Condition1             4.527   2.128    -0.20            
##           Condition2             4.115   2.028     0.38  0.08      
##           Condition1:Condition2  3.514   1.875     0.10  0.22  0.09
##  Item     (Intercept)            2.240   1.497                     
##  Item.1   Condition1             5.197   2.280                     
##  Item.2   Condition2             2.273   1.508                     
##  Item.3   Condition1:Condition2  2.619   1.618                     
##  Residual                        1.640   1.281                     
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.1912     1.0061 38.8892  10.129 1.84e-12 ***
## Condition1              4.7773     0.8223 15.9698   5.810 2.68e-05 ***
## Condition2             -2.9977     0.6082 22.0265  -4.929 6.24e-05 ***
## Condition1:Condition2   3.9174     0.6332 18.1802   6.187 7.37e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Check fit

  	npar	AIC	BIC	logLik	deviance	Chisq	Df	Pr(>Chisq)
  Max.M2	19	4621.094	4717.806	-2291.547	4583.094	NA	NA	NA
  Max.M1	25	4619.369	4746.621	-2284.685	4569.369	13.72516	6	0.0328616

• Model 1 was better
• Next, remove random effects on Subjects:

Max.M3<-lmer(DV_SS_RSlope_SSNoise_Items ~ Condition1*Condition2
              +(1+Condition1*Condition2||Subject)
              +(1+Condition1*Condition2|Item),
              data=DataSim8, REML=FALSE)
summary(Max.M3, corr=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## DV_SS_RSlope_SSNoise_Items ~ Condition1 * Condition2 + (1 + Condition1 *  
##     Condition2 || Subject) + (1 + Condition1 * Condition2 | Item)
##    Data: DataSim8
## 
##      AIC      BIC   logLik deviance df.resid 
##   4615.5   4712.2  -2288.7   4577.5     1181 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9901 -0.6311  0.0072  0.6479  3.5794 
## 
## Random effects:
##  Groups    Name                  Variance Std.Dev. Corr             
##  Subject   (Intercept)           23.583   4.856                     
##  Subject.1 Condition1             4.522   2.126                     
##  Subject.2 Condition2             4.105   2.026                     
##  Subject.3 Condition1:Condition2  3.494   1.869                     
##  Item      (Intercept)            2.212   1.487                     
##            Condition1             5.194   2.279     0.26            
##            Condition2             2.267   1.506    -0.33  0.46      
##            Condition1:Condition2  2.606   1.614     0.23 -0.61 -0.69
##  Residual                         1.640   1.281                     
## Number of obs: 1200, groups:  Subject, 30; Item, 10
## 
## Fixed effects:
##                       Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)            10.1912     1.0043 39.1091  10.148 1.63e-12 ***
## Condition1              4.7773     0.8219 15.9698   5.812 2.67e-05 ***
## Condition2             -2.9977     0.6074 22.0934  -4.935 6.10e-05 ***
## Condition1:Condition2   3.9174     0.6316 18.2527   6.202 7.02e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Check fit

## Data: DataSim8
## Models:
## Max.M3: DV_SS_RSlope_SSNoise_Items ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 || Subject) + (1 + Condition1 * Condition2 | Item)
## Max.M1: DV_SS_RSlope_SSNoise_Items ~ Condition1 * Condition2 + (1 + Condition1 * Condition2 | Subject) + (1 + Condition1 * Condition2 | Item)
##        npar    AIC    BIC  logLik deviance Chisq Df Pr(>Chisq)
## Max.M3   19 4615.5 4712.2 -2288.7   4577.5                    
## Max.M1   25 4619.4 4746.6 -2284.7   4569.4 8.088  6     0.2317

Model 3 is no worse a fit than Model 1.

Results of Simulation 3

• Model 3 is basically as good as model 1 (the maximal model), but we reduced the complexity and removed 6 random parameters. You will notice the t-values from models 1 and 3 are very similar. Those parameters were not doing much for us.