Exploratory Factor Analysis

EFA

• A multivariate method in which to determine the relationships and patterns between variables.
  • EFA examines a pattern of correlations/covariances between the items and tries to determine if they are influenced by the same or a different underlying factor.
  • EFA requires the data to be multivariate normal and have linear relationships
    • If you violate these assumptions, you can move to Multidimensional scaling (MDS), which is more flexible
  • EFA is different from Confirmatory Factor Analysis (CFA) in which you are trying to confirm a specific set of attempts to confirm how things should be related to one another using an SEM model
• EFA usages: (see Yong & Pearce, 2013)
  • 1. Develop Scales: such as Big 5 Personality
  • 2. Item’s Analysis: which test items go together (to test specific constructs)
  • 3. Dimensionality reduction: Which items/questions/features are most important (strength of which things bind together) and create “factor scores” representing underlying constructs for use in other analyses.

Collect items measured in the same units

• You might need to reverse score the items or recode/transform them
  • Usually Likert scales

Visualize the patterns in the data

• Helpful to look at the patterns before you go further

• Take data (BFI228) of the “study on personality and relationship satisfaction (Luo, 2005). The participants were 228 undergraduate students at a large public university in the US. The data were participants’ self-ratings on the 44 items of the Big Five Inventory (John, Donahue, & Kentle, 1991). These items are Likert variables: disagree strongly (1), disagree a little (2), neither agree nor disagree (3), agree a little (4), and agree strongly (5)”. Taken from the EFAutilities package.

library(psych)
library(corrplot)
library(EFAutilities)
data(BFI228)
DataSet<-as.data.frame(BFI228)
corrplot(cor(DataSet, method='spearman'), order = "hclust", 
         hclust.method = "ward.D2", tl.col='black', tl.cex=.75)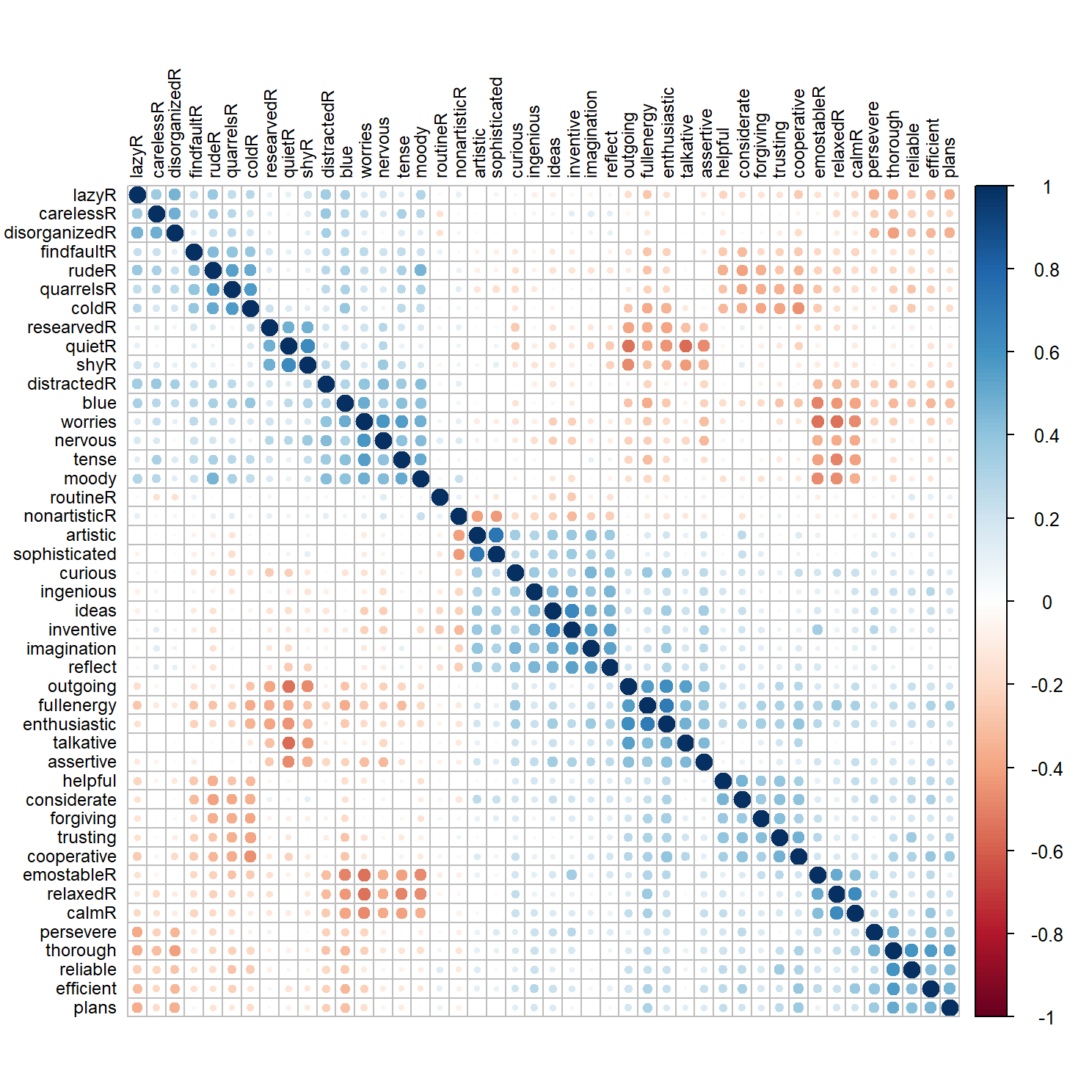 

Do I have enough data to proceed?

• Kaiser Meyer Olkin (KMO) Measure of Sampling Adequacy (Howard, 2016)
• You could remove anything below .6 and if the overall is below .6 you cannot do a EFA

KMO	Interpretation	Use?
0.00 to 0.50	Unacceptable	No
0.50 to 0.60	Miserable	No
0.60 to 0.70	Mediocre	Yes
0.70 to 0.80	Middling	Yes
0.80 to 0.90	Meritorious	Yes
0.90 to 1.00	Marvelous	Yes

KMO(DataSet)

## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = DataSet)
## Overall MSA =  0.83
## MSA for each item = 
##     talkative    researvedR    fullenergy  enthusiastic        quietR 
##          0.81          0.81          0.81          0.85          0.86 
##     assertive          shyR      outgoing    findfaultR       helpful 
##          0.91          0.78          0.84          0.87          0.83 
##     quarrelsR     forgiving      trusting         coldR   considerate 
##          0.84          0.82          0.81          0.83          0.83 
##         rudeR   cooperative      thorough     carelessR      reliable 
##          0.84          0.82          0.85          0.88          0.81 
## disorganizedR         lazyR     persevere     efficient         plans 
##          0.78          0.81          0.78          0.85          0.84 
##   distractedR          blue      relaxedR         tense       worries 
##          0.85          0.90          0.83          0.87          0.87 
##    emostableR         moody         calmR       nervous         ideas 
##          0.84          0.83          0.86          0.87          0.87 
##       curious     ingenious   imagination     inventive      artistic 
##          0.84          0.85          0.77          0.80          0.72 
##      routineR       reflect  nonartisticR sophisticated 
##          0.56          0.84          0.75          0.67

Remove an item

Remove routineR as it is below .6

DataSet.2 <- subset(DataSet, select = -c(routineR))

Get correlation/covariances matrix

• The type of correlation is important:
• If you have ordinal or nominal data you might want to switch from Pearson to Spearman, or poly- or tetra-choric correlations (for better fitting in IRT analysis)
• Most psychologists just ignore this and use Pearson as that is all SPSS can do (but we will use Spearman as it’s easy to compute)
  • Note: I have created the correlation matrix for the later factor analysis by hand. The psych will do it for you but read the function carefully to see what it defaults to doing

CM<-cor(DataSet.2, method = "spearman", use="complete.obs")

Select the number of factors

• You might have a specific number in mind, or it can be approximated from the data.

1. The Kaiser criterion: a number of factors equal to the number of the eigenvalues of the correlation matrix that is greater than one.
2. The “Scree test” is a lot of the eigenvalues of the correlation matrix in descending order

• What are eigenvalues? http://setosa.io/ev/eigenvectors-and-eigenvalues/

Selecting from the scree plot can be accomplished in a few different ways:

• Visually: When does the plot level off
• Parallel Analysis: (basically what random correlations would give you for the same number of subjects and items)
• Optimal Coordinate: extrapolation of the preceding eigenvalue by a regression line between the eigenvalue coordinates and the last eigenvalue coordinates
• Acceleration Factor: When the slope change most abruptly (elbow)
• Note: Don’t use the default of “1” heuristic that many people just apply.

library(nFactors)

ev <- eigen(CM) # get eigenvalues
ap <- parallel(subject=nrow(DataSet.2),var=ncol(DataSet.2),
  rep=100,cent=.05)
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea)
plotnScree(nS)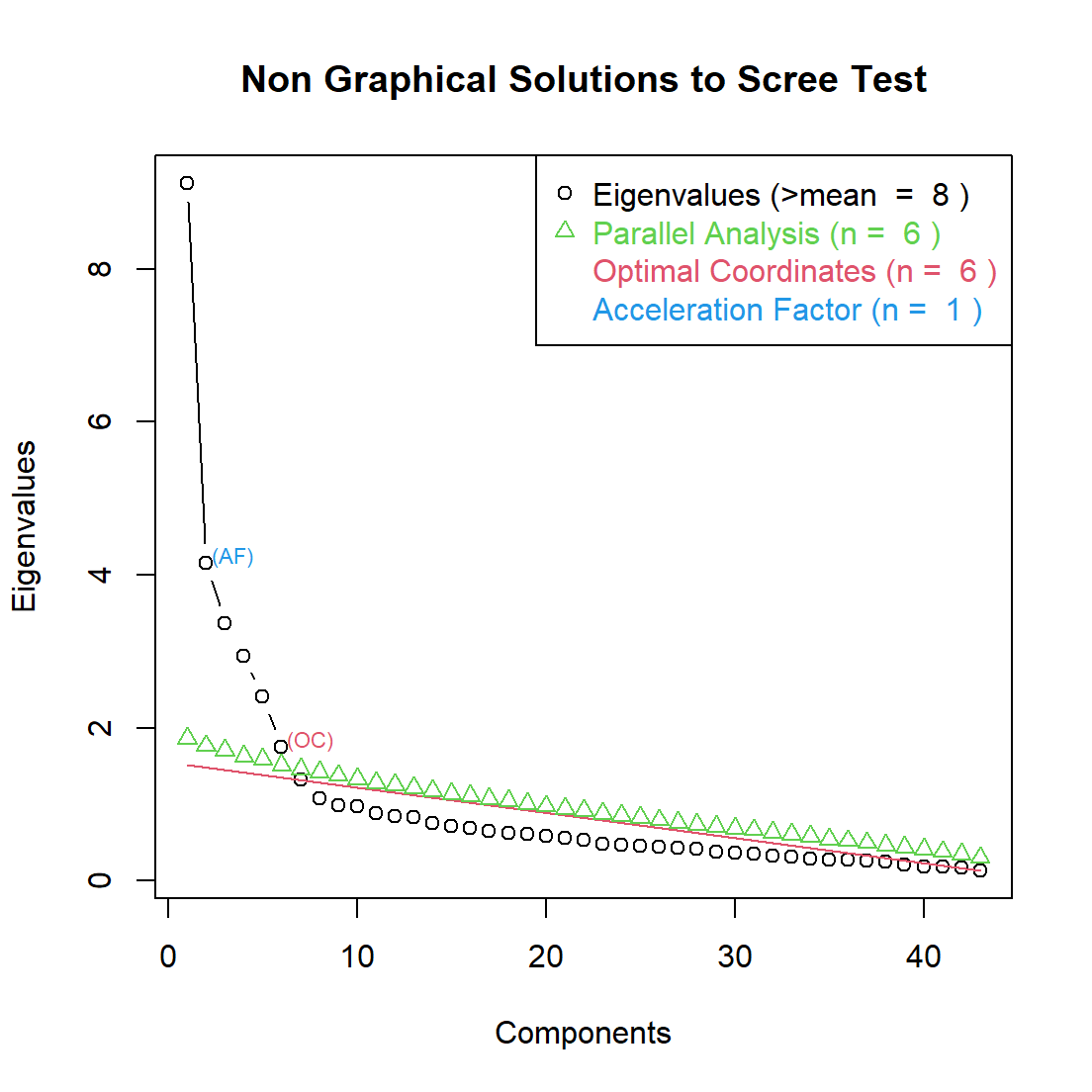

• Results suggest 6, but we will force a 5-factor solution to match the Big 5

Extract your initial solution

• Extraction methods: principal components analysis (PCA), maximum likelihood (ML), and principal axis factoring (PAF).
  • PCA is not a factor analysis method, but it is often used as it tries to put most of the variance into the first factor
  • ML is often used, but it’s sensitive to normality violations
    • ML allows comparison between models (Howard, 2016)
      
    • Note: if ML fitting fails you can do OLS fitted analysis (calling minres, which will give a similar response to ML and is the default in the psych package)
  • PAF is less sensitive to normality violation but less generalizable
    • Can be more accurate under assumption violations, but less flexible than ML (Howard, 2016)
      
  • There are many other types, such as Bayesian methods and methods for specific types of data (best to research each for your specific issue at hand). Today we will do ML fitting:

mle.Intial <- fa(CM,5, fm="mle",rotate="none")
print(mle.Intial$loadings, cutoff=0.2)

## 
## Loadings:
##               ML1    ML2    ML3    ML4    ML5   
## talkative      0.377  0.413 -0.366  0.264       
## researvedR    -0.388         0.413              
## fullenergy     0.676                            
## enthusiastic   0.653  0.330         0.247       
## quietR        -0.445 -0.351  0.497              
## assertive      0.483  0.334 -0.209              
## shyR          -0.411         0.512              
## outgoing       0.554  0.234 -0.383  0.302       
## findfaultR    -0.414                       0.238
## helpful        0.390         0.249  0.235       
## quarrelsR     -0.461  0.334 -0.228         0.311
## forgiving      0.387                0.266 -0.311
## trusting       0.433                0.348 -0.202
## coldR         -0.495  0.249        -0.337  0.351
## considerate    0.400         0.460  0.262 -0.256
## rudeR         -0.499  0.281                0.322
## cooperative    0.507                0.401       
## thorough       0.504 -0.242  0.265         0.481
## carelessR     -0.275  0.428                     
## reliable       0.432         0.246  0.237  0.285
## disorganizedR -0.260  0.378               -0.373
## lazyR         -0.427  0.265               -0.209
## persevere      0.385         0.309         0.344
## efficient      0.515         0.244         0.370
## plans          0.418                0.218  0.412
## distractedR   -0.425  0.301         0.250       
## blue          -0.589  0.324                     
## relaxedR       0.488 -0.305        -0.337       
## tense         -0.444  0.375  0.300  0.287       
## worries       -0.556  0.216         0.482       
## emostableR     0.535               -0.326       
## moody         -0.477  0.329         0.351       
## calmR          0.521 -0.201        -0.255       
## nervous       -0.467         0.315  0.438       
## ideas          0.439  0.452  0.243 -0.251       
## curious        0.423  0.309                     
## ingenious      0.351  0.350  0.295              
## imagination    0.335  0.546  0.256              
## inventive      0.411  0.454  0.331 -0.368       
## artistic       0.265  0.354  0.390              
## reflect        0.351  0.530  0.208              
## nonartisticR  -0.249                            
## sophisticated  0.204  0.275  0.416 -0.211       
## 
##                  ML1   ML2   ML3   ML4   ML5
## SS loadings    8.571 3.596 2.843 2.454 1.862
## Proportion Var 0.199 0.084 0.066 0.057 0.043
## Cumulative Var 0.199 0.283 0.349 0.406 0.449

fa.diagram(mle.Intial)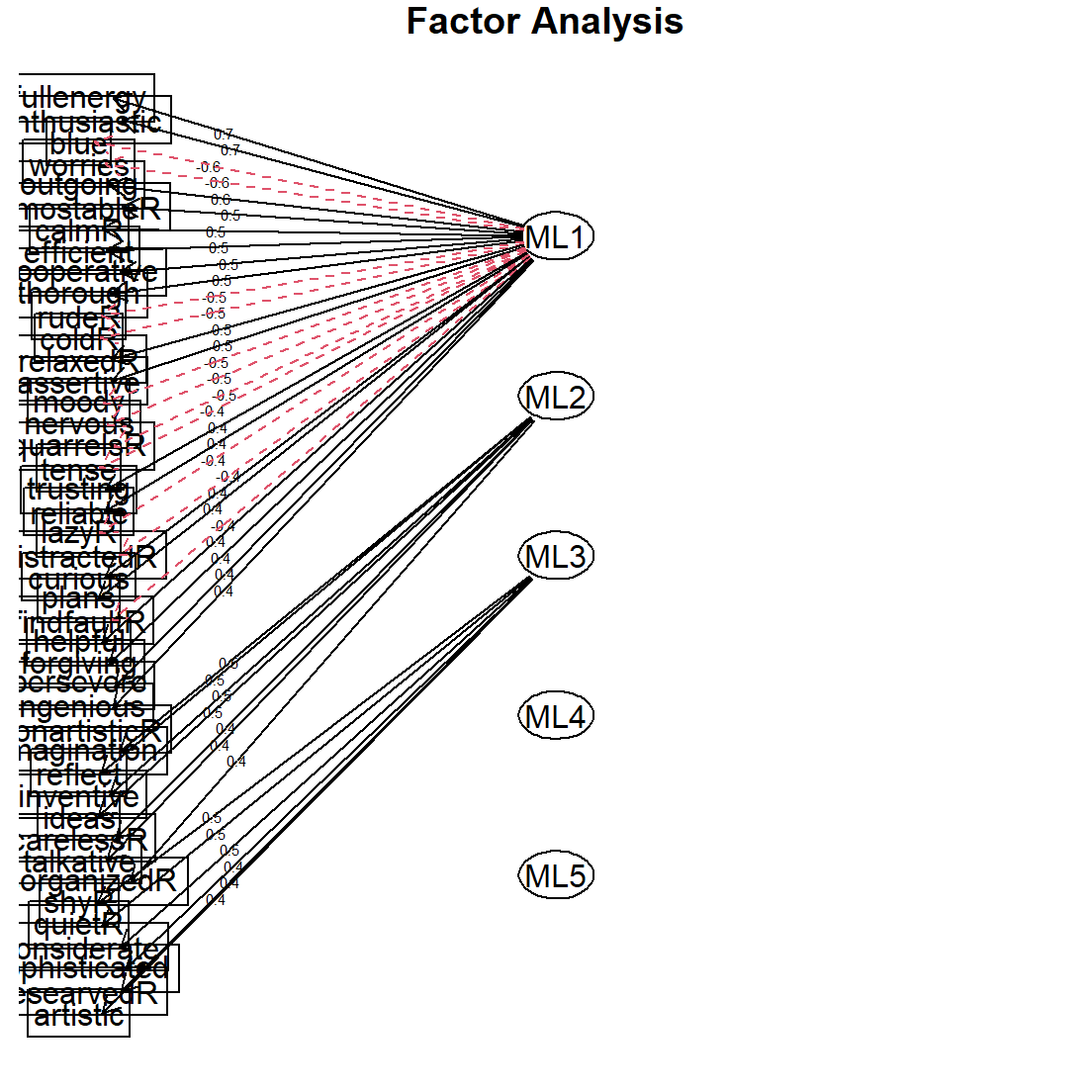

Rotate your factors to a final solution

• Think of each factor a dimension and the problem is there is a nearly infinite set of dimensions that could explain your data
• We need a way to help come up with a solution that is more interpretable (and reliable)
• By rotating your factors, you attempt to find a factor solution that is equal to that obtained in the initial extraction, but which has the most straightforward interpretation
• The simplest solution has 5 features (summarized in Abdi, 2003)
  • 1. each row contains at least one zero
  • 2. for each column, there are at least as many zeros as there are columns
  • 3. for any pair of factors, there are some variables with zero loadings on one factor and large loadings on the other factor
  • 4. for any pair of factors, there is a sizable proportion of zero loadings
  • 5. for any pair of factors, there is only a small number of large loadings
• There are many different types of rotation, but they all try to get the strongest effect on the small subset of items.

There are two families of rotations: - Orthogonal rotations: uncorrelated factors (e.g., varimax, quartimax, equimax) - Oblique rotations: produce correlated factors (e.g., promax)

• Varimax is the most popular orthogonal rotation: “simple solution means that each factor has a small number of large loadings and a large number of zero (or small) loadings” (Abdi, 2003)
  • Quartimax tries to find less factors and equimax balanced between varimax and quartimax

Orthogonal Rotation

• Loadings: We tend to consider a loading at between .3 or .4 (see Howard, 2016 for review)
  • Howard, 2016 recommends the .40–.30–.20 rule:
    • Primary factor above 0.40
    • Alternative factors below 0.30
    • Demonstrate a difference of 0.20 between their primary and alternative factor loadings

mle.VM <- fa(CM,5, fm="mle",rotate="varimax")
print(mle.VM$loadings, cutoff=0.2)

## 
## Loadings:
##               ML4    ML2    ML1    ML3    ML5   
## talkative                           0.707       
## researvedR     0.216               -0.546       
## fullenergy    -0.227         0.387  0.536       
## enthusiastic          0.296  0.417  0.605       
## quietR                             -0.781       
## assertive             0.319         0.526       
## shyR           0.218               -0.655       
## outgoing                     0.244  0.722       
## findfaultR     0.290        -0.420              
## helpful                      0.499              
## quarrelsR      0.278        -0.619              
## forgiving                    0.567              
## trusting                     0.570              
## coldR                       -0.687              
## considerate           0.280  0.626              
## rudeR          0.348        -0.572              
## cooperative                  0.567  0.218  0.281
## thorough                                   0.753
## carelessR      0.327                      -0.384
## reliable                     0.269         0.577
## disorganizedR                             -0.583
## lazyR          0.211        -0.212        -0.468
## persevere             0.266                0.530
## efficient                                  0.634
## plans                                      0.641
## distractedR    0.522                      -0.310
## blue           0.527        -0.267 -0.200 -0.287
## relaxedR      -0.646                            
## tense          0.696                            
## worries        0.747                            
## emostableR    -0.597  0.203  0.214              
## moody          0.688                            
## calmR         -0.530                       0.226
## nervous        0.634               -0.275       
## ideas                 0.688                     
## curious               0.444         0.235       
## ingenious             0.577                     
## imagination           0.689                     
## inventive             0.770                     
## artistic              0.603                     
## reflect               0.649         0.210       
## nonartisticR         -0.391                     
## sophisticated         0.557                     
## 
##                  ML4   ML2   ML1   ML3   ML5
## SS loadings    4.322 4.007 3.862 3.813 3.321
## Proportion Var 0.101 0.093 0.090 0.089 0.077
## Cumulative Var 0.101 0.194 0.284 0.372 0.449

fa.diagram(mle.VM)

Useful to examine the two factors that account for the most variance visually

• We will need to extract the factor loading

VM.load = mle.VM$loadings[,1:2]
plot(VM.load, type="n")
text(VM.load,labels=colnames(DataSet.2),cex=.75) # add variable names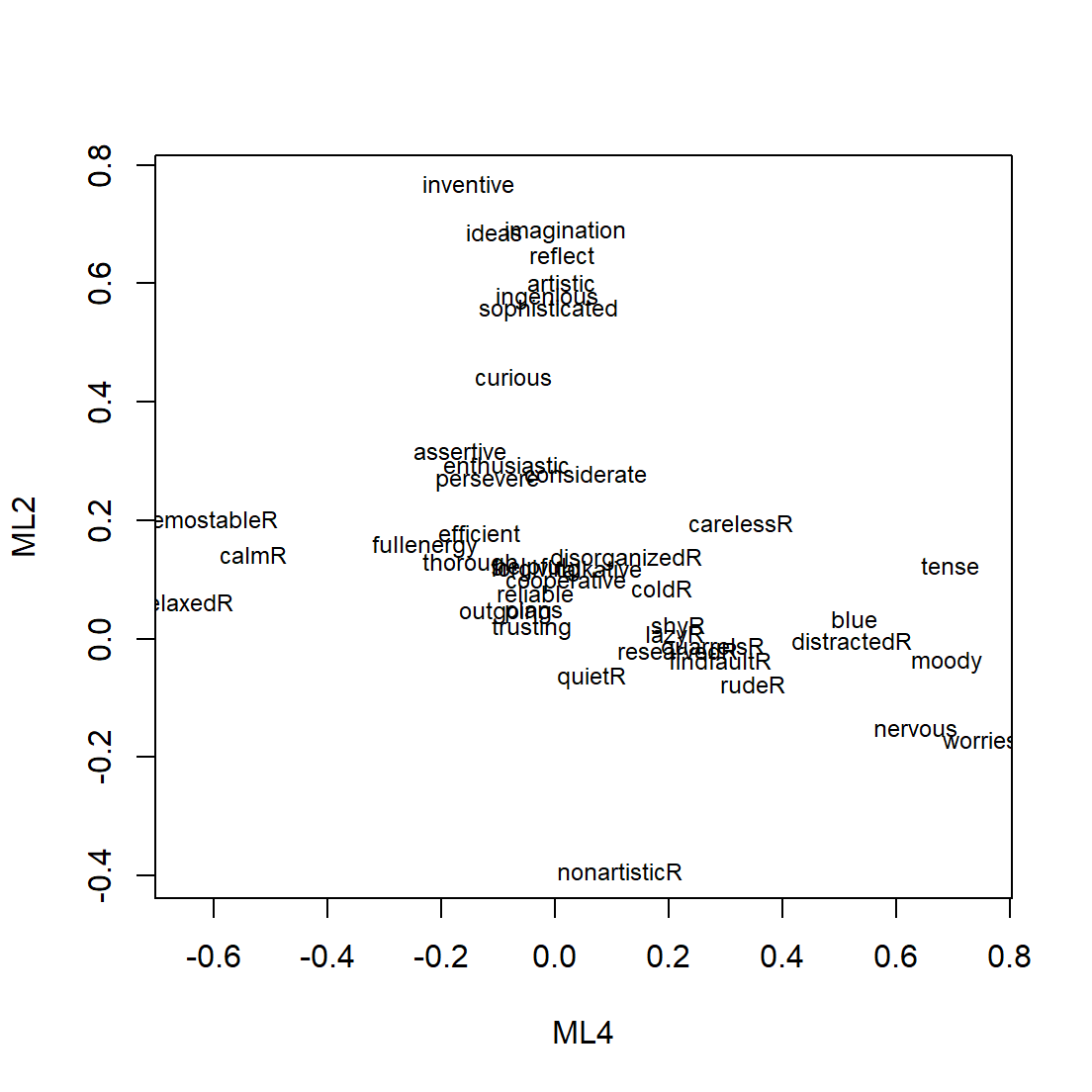

Oblique Rotation

• When we examine the promax, meaning now will allow for (small) correlation between factors. Oblique rotations were suggested by Thurstone
  • Promax performs a varimax rotation, and then it allows the factors to correlate through raising the factor loadings to a specified power (often 4) and useful for large datasets (see Howard, 2016)
  • Direct Oblimin, is another popular type, is harder to use as it requires you set a delta

mle.PM <- fa(CM,5, fm="mle",rotate="Promax")
print(mle.PM$loadings, cutoff=0.2)

## 
## Loadings:
##               ML4    ML2    ML1    ML3    ML5   
## talkative                           0.750       
## researvedR                         -0.548       
## fullenergy                   0.315  0.494       
## enthusiastic                 0.368  0.575       
## quietR                             -0.817       
## assertive             0.267         0.491       
## shyR                               -0.672       
## outgoing                            0.740       
## findfaultR     0.245        -0.425              
## helpful                      0.507              
## quarrelsR      0.202        -0.650              
## forgiving                    0.611              
## trusting                     0.590              
## coldR                       -0.734              
## considerate           0.215  0.661              
## rudeR          0.292        -0.589              
## cooperative                  0.555              
## thorough                                   0.813
## carelessR      0.270  0.248               -0.369
## reliable                                   0.601
## disorganizedR                             -0.635
## lazyR                                     -0.455
## persevere             0.223                0.578
## efficient                                  0.667
## plans                                      0.697
## distractedR    0.505                      -0.263
## blue           0.466                            
## relaxedR      -0.669                            
## tense          0.737                            
## worries        0.792                            
## emostableR    -0.617                            
## moody          0.733                            
## calmR         -0.514                            
## nervous        0.688         0.218              
## ideas                 0.688                     
## curious               0.411                     
## ingenious             0.572                0.216
## imagination           0.698                     
## inventive             0.793                     
## artistic              0.619                     
## reflect               0.651                     
## nonartisticR         -0.398                     
## sophisticated         0.583        -0.230       
## 
##                  ML4   ML2   ML1   ML3   ML5
## SS loadings    4.299 3.914 3.812 3.720 3.389
## Proportion Var 0.100 0.091 0.089 0.087 0.079
## Cumulative Var 0.100 0.191 0.280 0.366 0.445

fa.diagram(mle.PM)

Useful to examine the two factors that account for the most variance visually

• We will need to extract the factor loading

PM.load = mle.PM$loadings[,1:2]
plot(PM.load, type="n")
text(PM.load,labels=colnames(DataSet.2),cex=.75) # add variable names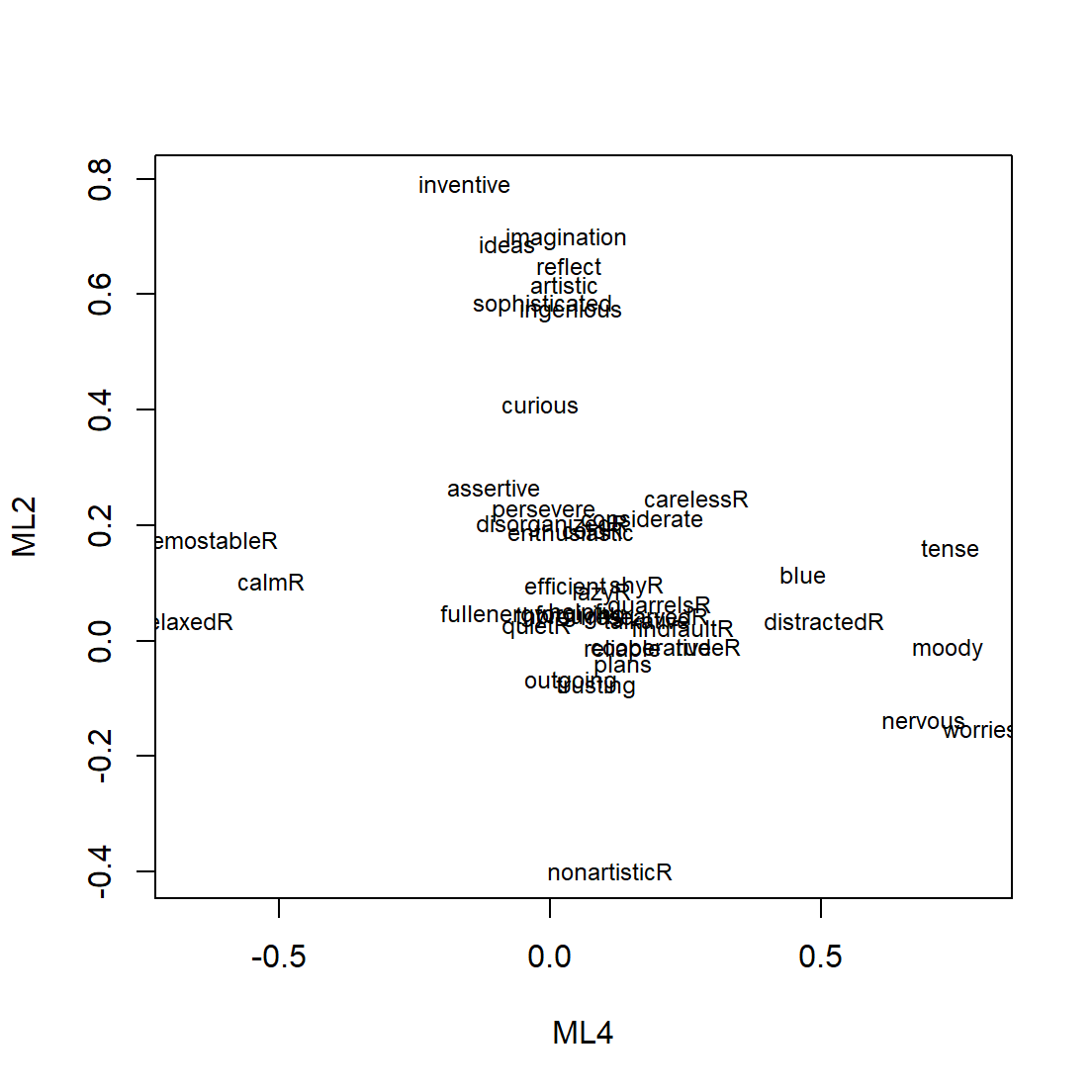

Interpret the Loadings

• This loading can be interpreted as like a part correlations (the variables are all controlled for)
• You have to name the construct based on the pattern of positive and negative loadings
• You could reverse score the loadings to make it easier
• Let’s name our factors from the varimax and promax and see what our 5 personality constructs might be

Extract factor scores

• You can construct factor scores for each subject and conduct additional analysis (in standardized units [z-scores])
• For example, you boiled down these items to 5 factors, you can run 5 regression on these constructs (they could be predictors or predicted)
• There are many ways to extract scores per person based on the factor analysis (how much each person fits with the construct), most common are:
  • Regression (aka Thurstone). Does not correct for bias in the estimation of the scores per person
  • Bartlett’s: which is an older method for correcting for bias in the estimation of the scores per person
  • ten Berge’s: corrects for bias and keeps the correlation matrix for oblique rotations

Regression

• Uses the estimated parameters from a factor analysis to define linear combinations of observed variables that generate factor scores. The scores may be correlated even when factors were set to be orthogonal

mle.VM.Score.R <- factor.scores(DataSet.2,mle.VM, method = "Thurstone")
#Cor
round(mle.VM.Score.R$r.scores,3)

##        ML4   ML2    ML1    ML3    ML5
## ML4  1.000 0.016 -0.033 -0.026 -0.023
## ML2  0.016 1.000  0.065  0.031  0.024
## ML1 -0.033 0.065  1.000  0.055  0.105
## ML3 -0.026 0.031  0.055  1.000  0.014
## ML5 -0.023 0.024  0.105  0.014  1.000

# Mean
round(apply(mle.VM.Score.R$scores,2, mean),3)

## ML4 ML2 ML1 ML3 ML5 
##   0   0   0   0   0

# SD
round(apply(mle.VM.Score.R$scores,2, sd),3)

##   ML4   ML2   ML1   ML3   ML5 
## 0.931 0.947 0.930 0.926 0.918

ten Berge’s

• Corrects for bias in the scores and keep the variables uncorrelated when factors are orthogonal

mle.VM.Score.TB <- factor.scores(DataSet.2,mle.VM, method = "tenBerge")
#Cor
round(mle.VM.Score.TB$r.scores,3)

##     ML4 ML2 ML1 ML3 ML5
## ML4   1   0   0   0   0
## ML2   0   1   0   0   0
## ML1   0   0   1   0   0
## ML3   0   0   0   1   0
## ML5   0   0   0   0   1

# Mean
round(apply(mle.VM.Score.TB$scores,2, mean),3)

## ML4 ML2 ML1 ML3 ML5 
##   0   0   0   0   0

# SD
round(apply(mle.VM.Score.TB$scores,2, sd),3)

## ML4 ML2 ML1 ML3 ML5 
##   1   1   1   1   1

• Also works with our oblique rotation

mle.PM.Score.TB <- factor.scores(DataSet.2,mle.PM, method = "tenBerge")
#Cor
round(mle.PM.Score.TB$r.scores,3)

##        ML4    ML2    ML1    ML3    ML5
## ML4  1.000 -0.109 -0.334 -0.309 -0.424
## ML2 -0.109  1.000  0.245  0.269  0.178
## ML1 -0.334  0.245  1.000  0.250  0.448
## ML3 -0.309  0.269  0.250  1.000  0.225
## ML5 -0.424  0.178  0.448  0.225  1.000

# Mean
round(apply(mle.PM.Score.TB$scores,2, mean),3)

## ML4 ML2 ML1 ML3 ML5 
##   0   0   0   0   0

# SD
round(apply(mle.PM.Score.TB$scores,2, sd),3)

## ML4 ML2 ML1 ML3 ML5 
##   1   1   1   1   1

References

Abdi, H. (2003). Factor rotations in factor analyses. Encyclopedia for Research Methods for the Social Sciences. Sage: Thousand Oaks, CA, 792-795.

Howard, M. C. (2016). A Review of Exploratory Factor Analysis Decisions and Overview of Current Practices: What We Are Doing and How Can We Improve?. International Journal of Human-Computer Interaction, 32(1), 51-62.

Yong, A. G., & Pearce, S. (2013). A beginner’s guide to factor analysis: Focusing on exploratory factor analysis. Tutorials in Quantitative Methods for Psychology, 9(2), 79-94.