Longitudinal

Longitudinal Designs

• Longitudinal generally means you measure a person over time. Thus, the person is the level 2 (the cluster) and Time is the level 1.
  • At least 3 measurements for that person: Longitudinal can be defined in seconds, minutes, days, weeks, years, or decades.
  • Time is repeated measure on the subject, but you are interested in charting how they change over time

Mixed Model framework for Longitudinal

• Mixed models have some major advantages over RM ANOVA approach to dealing with time
  • 1. Intercept differences: do different treatments have different baselines
  • 2. Slope differences between treatments
  • 3. Growth curves: Are slopes linear or curvilinear
    • 3a) Each subject can have a different slope and slope shape
  • 4. Time measurements do not need to be the same for each subject: Subject 1: Month 1,2,4,6, Subject 2: Month 2,3,5,7
    • 4a) This because you can have missing data in your measurements: in RM ANOVA this would mean you lose the whole subject
  • 5. You test for discontinuities in time: For example, treatment changes during the measurements (think elbow shaped slope)
    • Subjects have 3 baselines: Month 1, 2, 3 and at Month 4 they start treatment, and you have two more measurements. Thus you want to see if the slope during no treatment for that subject changes after treatment
      
  • 6. We can measure Time Fixed Covariates: Covariate does not change over the measurement period (DV = Depression score at each treatment, Covariate = Trait Anxiety level)
  • 7. We can measure Time Variable Covariates: Covariate that change over the measurement period (DV = Depression score at each treatment, Covariate = State Anxiety level during a therapy session)
  • 8. Interact Time Fixed and Time Variable covariates
  • 9. You can control the covariance structure and use autoregressive structures (but not in lme4)
  • 10. Deal with nested forms of Time: For example, month to month change in Anxiety levels, but you can also examine hour to hour Anxiety levels (nested in the month they were collected)

Simplest Type of Longitudinal Model

Children with ASD typically have difficulty with motor skill and poor interpersonal coordination. Their reduced ability to coordinate with people maybe be causing them to be left out of play with other children isolating them. Past efforts to improve their interpersonal coordination have often failed because children with ASD are overwhelmed by people. So training sessions often fail. However, children with ASD gravitate towards electronics and have been observed to be interested and comfortable with robots. Srinivasan et al., (2015) hypothesized that children with ASD might be better at coordinating with robots because a) children with ASD love robots, and b) robots are less threatening as they convey less information (not overwhelming the child). Srinivasan et al., (2015) found that having children “dance” with dancing robots improved their interpersonal coordination ability.

Today we will examine a simulated study of interpersonal coordination on 12 children with ASD. Each child underwent 6 training sessions (including the baseline where they had an ASD assessment to see where they were on the spectrum; Chlebowski et al. 2010). The children were asked to “dance” with an instructor and their parent in each of the 6 sessions. In the last part of the session their degree of coordination (from 0 - 1) with the new instructor who was in the room during the session, but did not dance. For half the children the instructor was human, and for the other half, the instructor was a robot.

Data

• As with all our other analysis, the data is in long format (for Longitudinal you might see it called period-period data)
  • Time is coded to start at 0 (baseline or first measurement).
  • Instructor (0,1): 0: Human; 1: Robot
  • Coordination (0-1): Degree of coordination (DV)
  • ASD: ASD spectrum score (possible covariate)
  • Download data

LongSim<-read.csv("Mixed/LongData1.csv")

Subject	Time	Instructor	Coordination	ASD
1	0	0	0.2220880	26.07486
1	1	0	0.2780595	26.07486
1	2	0	0.2701741	26.07486
1	3	0	0.1431913	26.07486
1	4	0	0.4037957	26.07486
1	5	0	0.3261772	26.07486

Coding

• Decisions have to be made about how to code Instructor
  • Dummy or effects code it? For today lets just dummy code our treatment

#Dummy
LongSim$Instructor.D<-factor(LongSim$Instructor,
                             levels = c(0,1),
                             labels = c("Human","Robot"))

• Decisions have to be made about how to code Time. Each again will change how we interpret our model. We will code it out now for later:
  • We can leave Time as is: it starts at 0 and progresses in the units of measurements
  • Center time Time: So there are 6 sessions (0-5), thus center is 2.5: So Session # - 2.5
  • (Note: yes you can Zscore time or Zscore and NOT center as well)

# Centered
LongSim$Time.C<-scale(LongSim$Time, scale=F, center=T)[,]

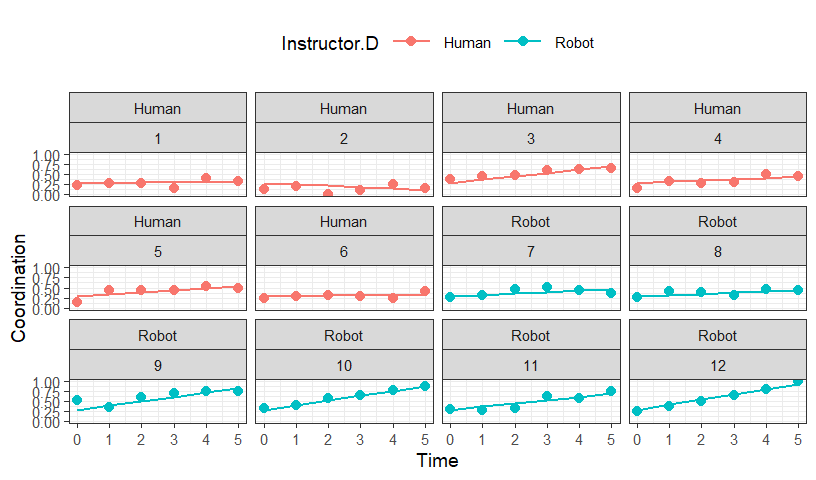
Spaghetti Plots

• Longitudinal Models are best assessed with spaghetti plots. When you have a small number of subjects, you can plot it as “facets.”
• We will plot each person in a facet and add their linear model for each subject

# Make sure that subject is a factor
LongSim$Subject<-as.factor(LongSim$Subject)

Speg.1<-ggplot(data = LongSim, aes(x=Time,y=Coordination))+
  facet_wrap(~Subject)+
  geom_point(aes(color=Instructor.D))+
  geom_smooth(method='lm', se=FALSE,aes(color=Instructor.D))+
  xlab("Time")+ylab("Coordination")+
  theme_bw()+
  theme(legend.position = "top")
Speg.1

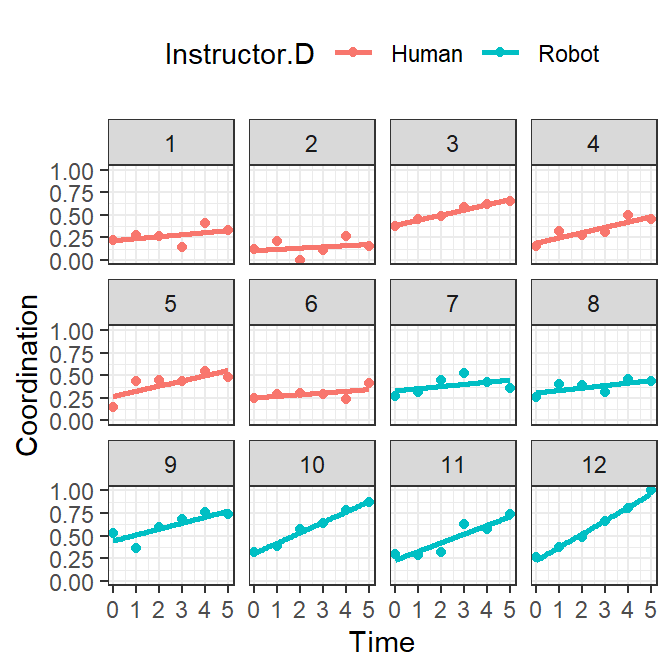
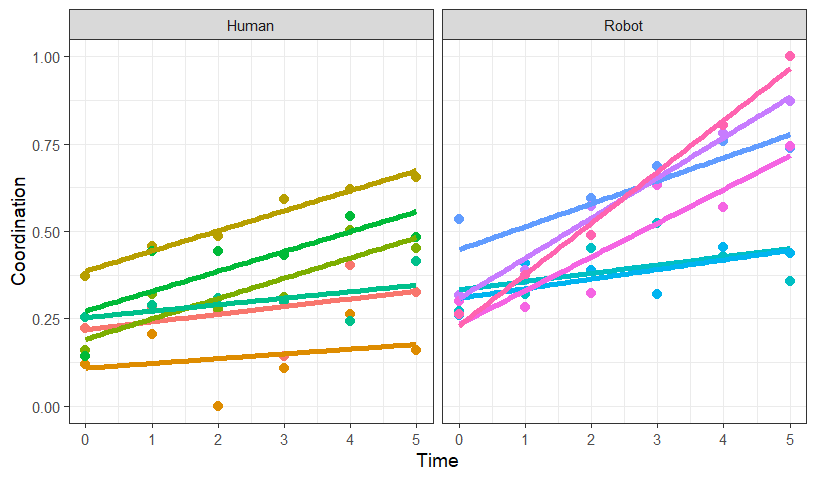
• If you have too many subjects, you can plot the results like this instead
• On the left, you can fit a regression per subject, on the right you plot lines instead of the slope

theme_set(theme_bw(base_size = 7, base_family = ""))

Speg.2<-ggplot(data = LongSim, aes(x=Time,y=Coordination, group=Subject, color=Subject))+
  facet_wrap(~Instructor.D)+
  geom_point()+
  geom_smooth(method='lm', se=FALSE)+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "none")
Speg.2

Speg.3<-ggplot(data = LongSim, aes(x=Time,y=Coordination, group=Subject, color=Subject))+
  facet_wrap(~Instructor.D)+
  geom_point()+
  geom_line()+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "none")
Speg.3

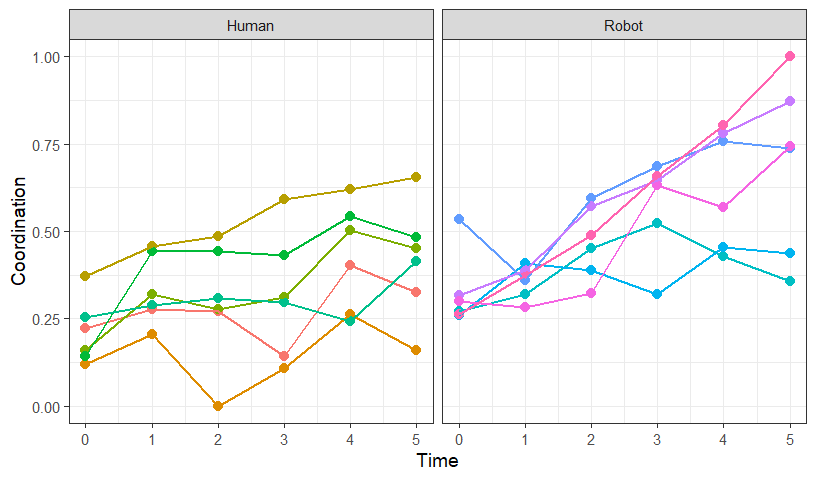
Modeling to Examine Random Structure

• The subject is the Level 2 variable (just like in our repeated measures mixed models)
• We can show that via our ICC analysis

Intercepts only model

Null<-lmer(Coordination ~ 1+(1|Subject), data=LongSim, REML=FALSE)
sjstats::icc(Null)

## # Intraclass Correlation Coefficient
## 
##     Adjusted ICC: 0.420
##   Unadjusted ICC: 0.420

Intercepts only plot

• Predict out the model results
• Dots = Real data
• Line = Predicted result

theme_set(theme_bw(base_size = 7, base_family = ""))

LongSim$Null<-predict(Null, newdata=LongSim)

Speg.Null.1<-ggplot(data = LongSim)+
  facet_wrap(~Subject)+
  geom_point(aes(x=Time,y=Coordination,color=Instructor.D))+
  geom_line(aes(x=Time,y=Null, color=Instructor.D))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "top")
Speg.Null.1

Speg.Null.2<-ggplot(data = LongSim)+
  facet_wrap(~Instructor.D)+
  geom_point(aes(x=Time,y=Coordination, group=Subject,color=Subject))+
  geom_line(aes(x=Time,y=Null,group=Subject,color=Subject))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "none")
Speg.Null.2

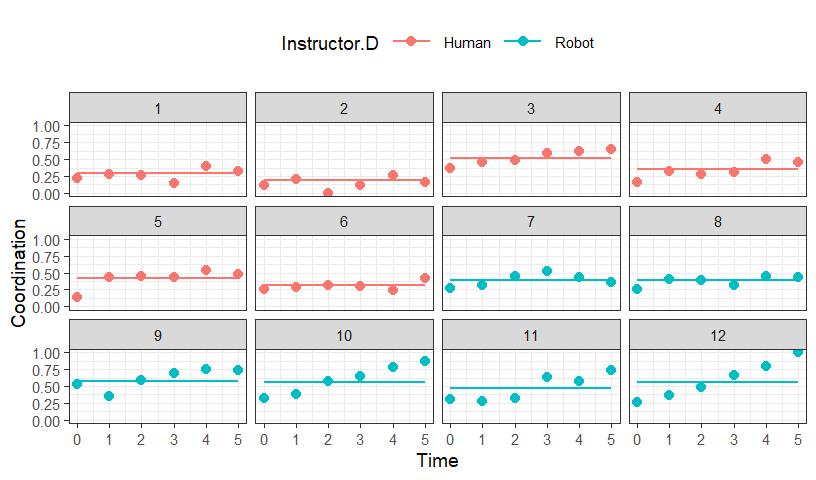
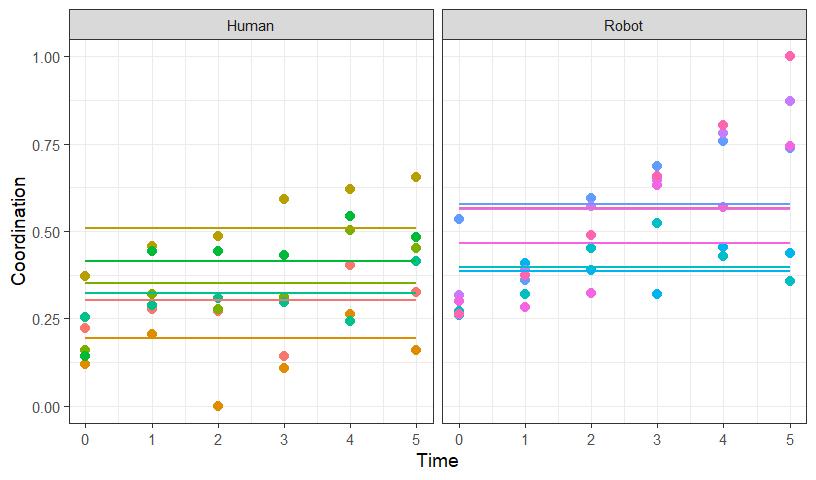- Notice that each subject has their own intercept, but no slope

Random Intercepts and Slopes Model

• We will let the intercept and Time vary relative to each subject: (1+Time|Subject)
  • Note you can block the correlation between the slope/intercept like before if the correlation is -1/1: (1+Time||Subject)

RISlope<-lmer(Coordination ~ 1+(1+Time|Subject), data=LongSim, REML=FALSE)
summary(RISlope)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ 1 + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -102.0    -90.6     56.0   -112.0       67 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.21989 -0.52703  0.01245  0.55970  2.00199 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 0.004804 0.06931      
##           Time        0.004751 0.06893  0.42
##  Residual             0.005488 0.07408      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##             Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)  0.26005    0.02481 12.00035   10.48 2.15e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Random Intercept and Slopes Plot

• Predict out the model results
• Dots = Real data
• Line = Predicted result

theme_set(theme_bw(base_size = 7, base_family = ""))

LongSim$RISlope<-predict(RISlope, newdata=LongSim)
Speg.R.I.Slope.1<-ggplot(data = LongSim)+
  facet_wrap(~Subject)+
  geom_point(aes(x=Time,y=Coordination, color=Instructor.D))+
  geom_line(aes(x=Time,y=RISlope, color=Instructor.D))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "top")
Speg.R.I.Slope.1

Speg.R.I.Slope.2<-ggplot(data = LongSim)+
  facet_wrap(~Instructor.D)+
  geom_point(aes(x=Time,y=Coordination, group=Subject,color=Subject))+
  geom_line(aes(x=Time,y=RISlope,group=Subject,color=Subject))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "none")
Speg.R.I.Slope.2

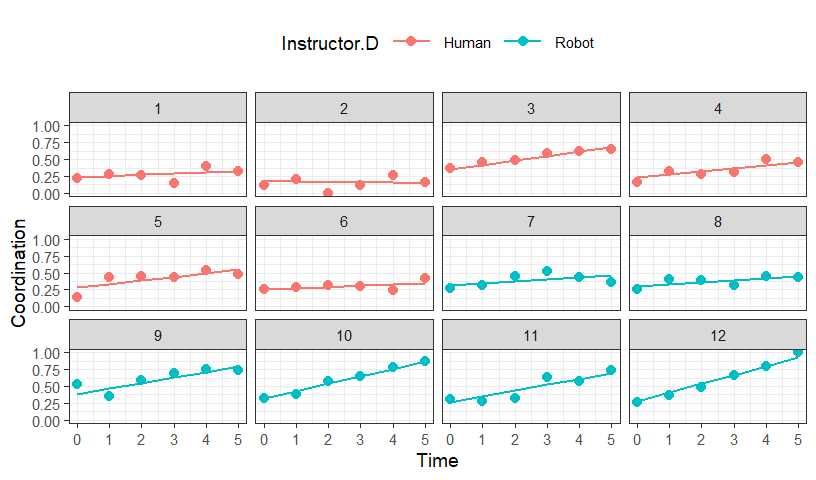
Random Slopes Only Model

• It could be there is no random intercept, so you can remove it (but you need to have a reason)
• We will let Time vary relative to each subject: (0+Time|Subject)

RSlope<-lmer(Coordination ~ 1+(0+Time|Subject), data=LongSim, REML=FALSE)
summary(RSlope)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ 1 + (0 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##    -99.3    -92.5     52.6   -105.3       69 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.54802 -0.53178 -0.00811  0.59543  2.92944 
## 
## Random effects:
##  Groups   Name Variance Std.Dev.
##  Subject  Time 0.005376 0.07332 
##  Residual      0.007289 0.08538 
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##             Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)  0.28463    0.01739 65.05840   16.36   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

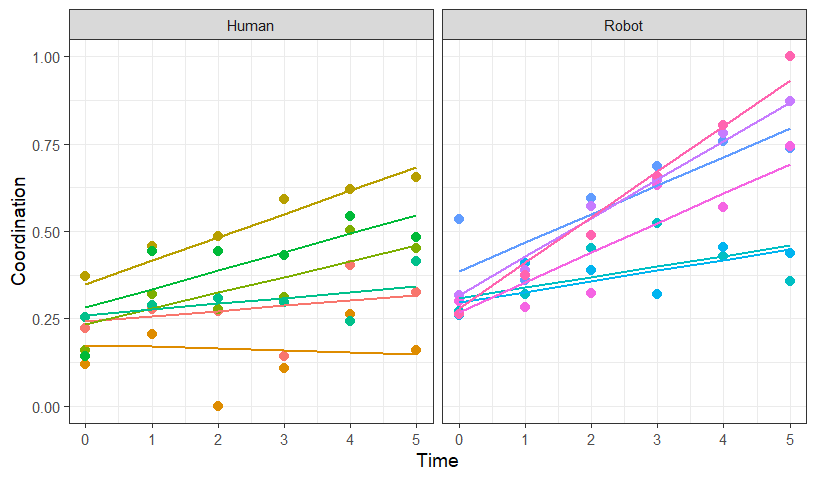
Random Slopes Only Plot

• Predict out the model results
• Dots = Real data
• Line = Predicted result

theme_set(theme_bw(base_size = 7, base_family = ""))

LongSim$RSlope<-predict(RSlope, newdata=LongSim)

Speg.R.Slope.1<-ggplot(data = LongSim)+
  facet_wrap(Instructor.D~Subject)+
  geom_point(aes(x=Time,y=Coordination, color=Instructor.D))+
  geom_line(aes(x=Time,y=RSlope, color=Instructor.D))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "top")
Speg.R.Slope.1

Speg.R.Slope.2<-ggplot(data = LongSim)+
  facet_wrap(~Instructor.D)+
  geom_point(aes(x=Time,y=Coordination, group=Subject,color=Subject))+
  geom_line(aes(x=Time,y=RSlope,group=Subject,color=Subject))+
  xlab("Time")+ylab("Coordination")+
  theme(legend.position = "none")
Speg.R.Slope.2

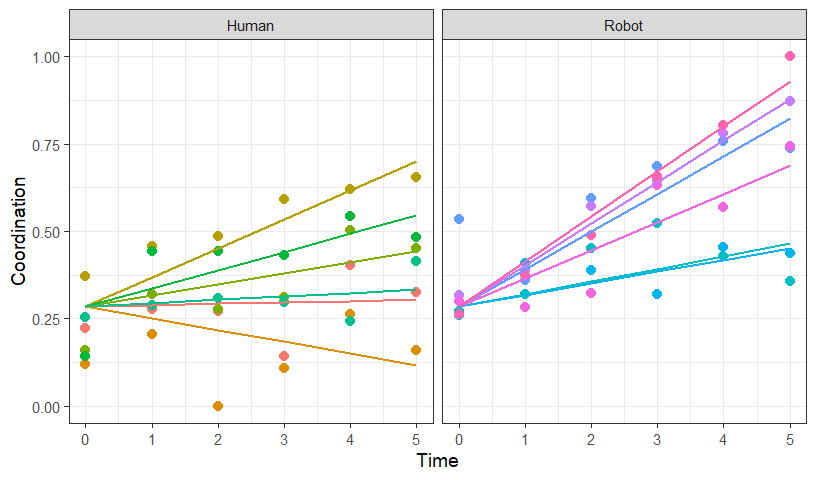
• Note: The intercepts for each subject are the same.
• You can also guess that this model will not be a good fit as the last one, which we can test:

anova(RSlope,RISlope)

## Data: LongSim
## Models:
## RSlope: Coordination ~ 1 + (0 + Time | Subject)
## RISlope: Coordination ~ 1 + (1 + Time | Subject)
##         npar      AIC     BIC logLik deviance  Chisq Df Pr(>Chisq)  
## RSlope     3  -99.287 -92.457 52.643  -105.29                       
## RISlope    5 -102.000 -90.617 56.000  -112.00 6.7134  2    0.03485 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Modeling for Results

• The goal above was to understand the random effects. This is useful if you want to understand your data, but when you move to modeling for publication you will want to set your random effects and move to fixed effect testing
• The most obvious structure for most longitudinal (2 level) data is to use random slopes and intercepts (watch that correlation between them)
• We will now also explore the different coding schemes to understand the models

Non-Centered Time & Dummy coded Instructor

• Note: because Instructor is 0/1 coded you can also enter that into the model instead of it as a factor (you will get the same answer)

Main effects

MainEffect.1<-lmer(Coordination ~ Time+Instructor.D+(1+Time|Subject), data=LongSim, REML=FALSE)
summary(MainEffect.1, correlation=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time + Instructor.D + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -113.8    -97.9     63.9   -127.8       65 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.15774 -0.56020  0.04558  0.61775  1.91569 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 0.003360 0.05796      
##           Time        0.001327 0.03642  0.15
##  Residual             0.005488 0.07408      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                   Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)        0.23232    0.03206 12.08500   7.247  9.8e-06 ***
## Time               0.05852    0.01169 11.99995   5.005 0.000307 ***
## Instructor.DRobot  0.08358    0.04509 11.99994   1.854 0.088498 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

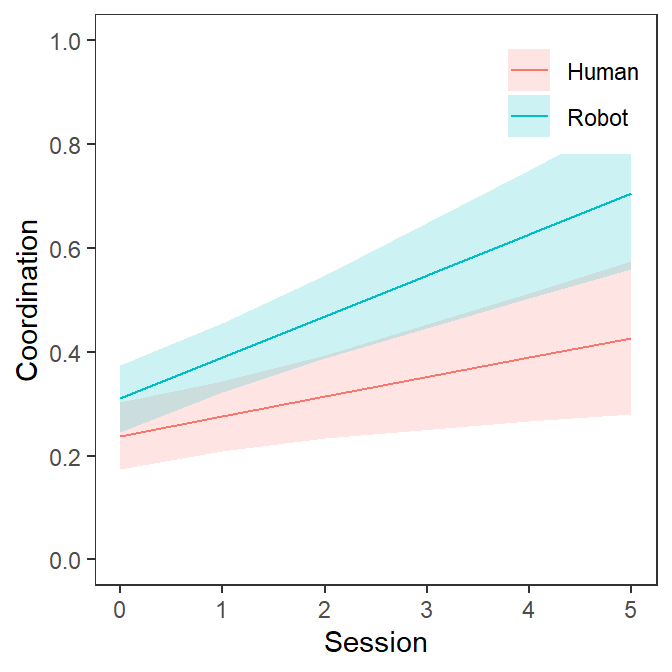
Interpretation

• Time: After each session, the kids get are better at coordinating regardless of Instruction (the estimate is the slope over sessions)
• Instructor.DRobot: t < 1.96 (so not significant). Had it been significant it would mean that kids who had the robot instructor had overall higher coordination [averaged over all session] (the estimate reported is the difference between human and robot)

Interaction

Interaction.1<-lmer(Coordination ~ Time*Instructor.D+(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Interaction.1, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time * Instructor.D + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -115.5    -97.3     65.7   -131.5       64 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.17344 -0.56178  0.04976  0.64212  2.08058 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev. Corr
##  Subject  (Intercept) 0.0033241 0.05766      
##           Time        0.0008965 0.02994  0.25
##  Residual             0.0054877 0.07408      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                        Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)             0.23829    0.03214 12.00007   7.414 8.12e-06 ***
## Time                    0.03777    0.01420 11.99972   2.660   0.0208 *  
## Instructor.DRobot       0.07163    0.04546 12.00007   1.576   0.1411    
## Time:Instructor.DRobot  0.04148    0.02008 11.99972   2.065   0.0612 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretation

• Time: slope over sessions for kids who had the human instructor.
  
• Instructor.DRobot: It is the difference between human and robot when Time = 0 [Baseline].
  • To prove this we can fit the model and subtract the fitted values: Robot @ Time 0 - Human @ Time 0

library(effects)
effect(c("Time*Instructor.D"),Interaction.1)

Time	Instructor.D	fit	se	lower	upper
0	Human	0.2383	0.0321	0.1742	0.3024
1	Human	0.2761	0.0334	0.2093	0.3428
2	Human	0.3138	0.0401	0.2338	0.3938
4	Human	0.3894	0.0616	0.2665	0.5123
5	Human	0.4272	0.0741	0.2793	0.5751
0	Robot	0.3099	0.0321	0.2458	0.3741
1	Robot	0.3892	0.0334	0.3224	0.4559
2	Robot	0.4684	0.0401	0.3884	0.5484
4	Robot	0.6269	0.0616	0.5040	0.7499
5	Robot	0.7062	0.0741	0.5583	0.8541

- Estimate of **Instructor.DRobot**: 0.3099211 - 0.2382928 = 0.0716283
    - Note: *You are missing the simple effect of Human @ Time 0*. Relevel instructor to test if you need to know.

• Time:Instructor.DRobot: slope over sessions difference = slope @ robot instructor - slope @ human instructor

Centered Time & Dummy coded Instructor

• Note: Because Instructor is 0/1 coded you can also enter that into the model instead of it as factor (you will get the same answer)

Main effects

MainEffect.2<-lmer(Coordination ~ Time.C+Instructor.D+(1+Time|Subject), data=LongSim, REML=FALSE)
summary(MainEffect.2, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time.C + Instructor.D + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -113.8    -97.9     63.9   -127.8       65 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.15774 -0.56020  0.04558  0.61775  1.91569 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 0.003360 0.05796      
##           Time        0.001327 0.03642  0.15
##  Residual             0.005488 0.07408      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                   Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)        0.37861    0.04105 14.18874   9.223 2.26e-07 ***
## Time.C             0.05852    0.01169 11.99995   5.005 0.000307 ***
## Instructor.DRobot  0.08358    0.04509 11.99994   1.854 0.088498 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretation

• Same as non-centered

Interaction

• Now things will change because the zero-point in time is now the middle of the session (not the baseline)

Interaction.2<-lmer(Coordination ~ Time.C*Instructor.D+(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Interaction.2, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time.C * Instructor.D + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -115.5    -97.3     65.7   -131.5       64 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.17344 -0.56178  0.04976  0.64212  2.08058 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev. Corr
##  Subject  (Intercept) 0.0033241 0.05766      
##           Time        0.0008965 0.02994  0.25
##  Residual             0.0054877 0.07408      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                          Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)               0.33273    0.04476 11.99999   7.434  7.9e-06 ***
## Time.C                    0.03777    0.01420 11.99972   2.660   0.0208 *  
## Instructor.DRobot         0.17533    0.06329 11.99999   2.770   0.0170 *  
## Time.C:Instructor.DRobot  0.04148    0.02008 11.99972   2.065   0.0612 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretation

• Time: slope for kids who had the human instructor.
  
• Instructor.DRobot: It is the difference between human and robot when Time = 0. But remember Time 0 equals the Middle Session!
  • To prove this, we can fit the model and subtract the fitted values: Robot @ Time 0 - Human @ Time 0 [Middle session]

effect(c("Time.C*Instructor.D"),Interaction.2)

Time.C	Instructor.D	fit	se	lower	upper
-2	Human	0.2572	0.0320	0.1933	0.3211
-1	Human	0.2950	0.0362	0.2227	0.3672
0	Human	0.3327	0.0448	0.2434	0.4220
1	Human	0.3705	0.0556	0.2595	0.4816
2	Human	0.4083	0.0678	0.2730	0.5435
-2	Robot	0.3495	0.0320	0.2857	0.4134
-1	Robot	0.4288	0.0362	0.3565	0.5011
0	Robot	0.5081	0.0448	0.4188	0.5974
1	Robot	0.5873	0.0556	0.4763	0.6984
2	Robot	0.6666	0.0678	0.5313	0.8018

- Estimate of **Instructor.DRobot**: 0.5080641 - 0.3327298 = 0.1753344

• Time:Instructor.DRobot: slope over sessions difference = slope @ robot instructor - slope @ human instructor

Summary

• To center time or not center time?
• This all depends on what story you need to tell
• In the interaction model:
  • if you don’t center time, you are talking about the baseline. In this case, it seems very useful to be able to say the kids with ASD started out at the same level of coordination and over time their slopes changed
  • if you center time you are talking about the middle session, I find this less useful for the question at hand, but keep it in mind that you can examine it this way

Plot our Final Model

• We can use the effects package and ggplot to plot the fitted model

library(effects)
Fitted.I1<-effect(c("Time*Instructor.D"),Interaction.1)
Fitted.I1<-as.data.frame(Fitted.I1)

Fitted.Plot<-ggplot(data = Fitted.I1, aes(x=Time,y=fit, group=Instructor.D))+
  geom_line(aes(color=Instructor.D))+
  geom_ribbon(aes(ymin=lower,ymax=upper,fill=Instructor.D),alpha=.2)+
  xlab("Session")+ylab("Coordination")+
  scale_y_continuous(lim=c(0,1),breaks = seq(0, 1,.2)) +
  theme_bw()+
  theme(legend.position = c(.85,.875),
        legend.title = element_blank(),
        panel.grid.major = element_line(linetype = "blank"),
        panel.grid.minor = element_line(linetype = "blank"))
Fitted.Plot

Fixed Covariates

• We had a covariate: each kids autism spectrum score.
• We can simply add it to our model if we want to control for it, but you really should center it so you intercept does not change.

LongSim$ASD.C<-scale(LongSim$ASD, scale=F, center=T)[,]

• You can add it to your model just as any regression

Cov1.Model<-lmer(Coordination ~ Time*Instructor.D+ASD.C
                +(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Cov1.Model, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time * Instructor.D + ASD.C + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -125.0   -104.5     71.5   -143.0       63 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.13957 -0.60777  0.05259  0.66668  1.77972 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 0.001085 0.03294      
##           Time        0.001052 0.03244  1.00
##  Residual             0.004844 0.06960      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                          Estimate Std. Error         df t value Pr(>|t|)    
## (Intercept)             0.2739315  0.0261886 18.4814776  10.460 3.39e-09 ***
## Time                    0.0377748  0.0148838 12.3504929   2.538 0.025558 *  
## Instructor.DRobot       0.0003509  0.0391905 19.1578812   0.009 0.992948    
## ASD.C                  -0.0657266  0.0167110 25.5959845  -3.933 0.000569 ***
## Time:Instructor.DRobot  0.0414824  0.0210488 12.3504929   1.971 0.071583 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

Note: the correlation between the intercept and slope = 1, so we should block that moving forward and we would go back and block it in prior models to they are all have the same random structure. For now we will ignore it and move on

anova(Interaction.1,Cov1.Model)

## Data: LongSim
## Models:
## Interaction.1: Coordination ~ Time * Instructor.D + (1 + Time | Subject)
## Cov1.Model: Coordination ~ Time * Instructor.D + ASD.C + (1 + Time | Subject)
##               npar     AIC      BIC logLik deviance  Chisq Df Pr(>Chisq)    
## Interaction.1    8 -115.48  -97.265 65.739  -131.48                         
## Cov1.Model       9 -124.95 -104.462 71.476  -142.95 11.474  1  0.0007059 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Our slope is no longer significant, meaning the covariate might be explaining some of our interaction at the mean level of ASD score. This is suggestive of 3-way interaction.

Cov2.Model<-lmer(Coordination ~ Time*Instructor.D*ASD.C
                +(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Cov2.Model, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time * Instructor.D * ASD.C + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -127.7   -100.4     75.9   -151.7       60 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.25728 -0.53957 -0.00054  0.73048  1.68226 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev. Corr
##  Subject  (Intercept) 0.0005812 0.02411      
##           Time        0.0004871 0.02207  1.00
##  Residual             0.0047984 0.06927      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                               Estimate Std. Error        df t value Pr(>|t|)
## (Intercept)                   0.290973   0.027451 25.063026  10.600 9.49e-11
## Time                          0.042820   0.013615 13.221798   3.145  0.00761
## Instructor.DRobot            -0.005657   0.037056 25.063026  -0.153  0.87989
## ASD.C                        -0.097154   0.028438 25.063026  -3.416  0.00217
## Time:Instructor.DRobot        0.051314   0.018379 13.221798   2.792  0.01506
## Time:ASD.C                   -0.009305   0.014105 13.221798  -0.660  0.52075
## Instructor.DRobot:ASD.C       0.051776   0.034086 25.063026   1.519  0.14128
## Time:Instructor.DRobot:ASD.C  0.036742   0.016906 13.221798   2.173  0.04849
##                                 
## (Intercept)                  ***
## Time                         ** 
## Instructor.DRobot               
## ASD.C                        ** 
## Time:Instructor.DRobot       *  
## Time:ASD.C                      
## Instructor.DRobot:ASD.C         
## Time:Instructor.DRobot:ASD.C *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

anova(Cov1.Model,Cov2.Model)

## Data: LongSim
## Models:
## Cov1.Model: Coordination ~ Time * Instructor.D + ASD.C + (1 + Time | Subject)
## Cov2.Model: Coordination ~ Time * Instructor.D * ASD.C + (1 + Time | Subject)
##            npar     AIC     BIC logLik deviance  Chisq Df Pr(>Chisq)  
## Cov1.Model    9 -124.95 -104.46 71.476  -142.95                       
## Cov2.Model   12 -127.74 -100.42 75.872  -151.74 8.7914  3     0.0322 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

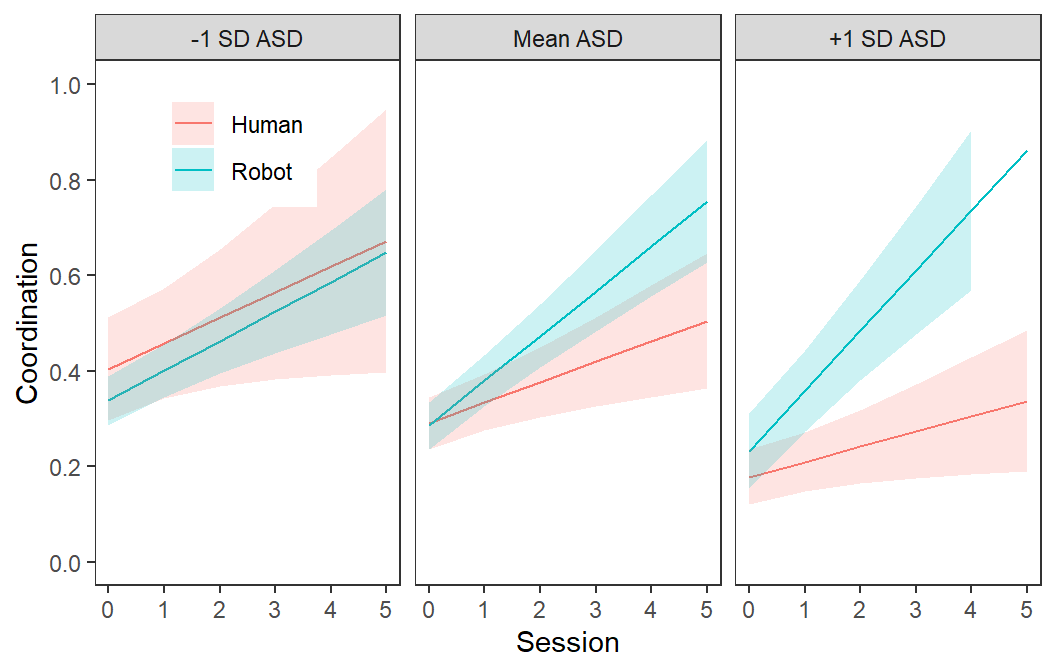
• The three way improved the model fit.
• Time:Instructor.DRobot: is the slope over sessions difference = slope @ robot instructor - slope @ human instructor [@ at the average ASD level]
• Time:Instructor.DRobot:ASD.C: is the slope over sessions difference = slope @ robot instructor - slope @ human instructor [as a function of ASD score]
  • So the slope difference between robot and human instructor is getting larger as ASD level increases. See the plot below to understand this:

Plot 3-Way

• We will plot it like any other interaction in a regression involving two continuous variables
• We will need to find 1 SD above/below the mean of the covariate (which was mean centered)

SDN1<- -sd(LongSim$ASD.C)
SDP1<- +sd(LongSim$ASD.C)

Fitted.Cov2<-effect(c("Time*Instructor.D*ASD.C"),Cov2.Model, 
                    xlevel=list(Time=seq(0,5,1),
                                ASD.C=c(SDN1,0,SDP1)))
Fitted.Cov2<-as.data.frame(Fitted.Cov2)

Fitted.Cov2$ASD<-factor(Fitted.Cov2$ASD.C, 
                           levels=c(SDN1,0,SDP1),
                           labels=c("-1 SD ASD","Mean ASD","+1 SD ASD"))

Fitted.Plot.2<-ggplot(data = Fitted.Cov2, aes(x=Time,y=fit, group=Instructor.D))+
  facet_grid(~ASD)+
  geom_line(aes(color=Instructor.D))+
  geom_ribbon(aes(ymin=lower,ymax=upper,fill=Instructor.D),alpha=.2)+
  xlab("Session")+ylab("Coordination")+
  scale_y_continuous(lim=c(0,1),breaks = seq(0, 1,.2)) +
  theme_bw()+
  theme(legend.position = c(.15,.85),
        legend.title = element_blank(),
        panel.grid.major = element_line(linetype = "blank"),
        panel.grid.minor = element_line(linetype = "blank"))
Fitted.Plot.2

Test of Simple Interactions

• If you want to know if the interaction is significant at each level of ASD score, you simply have to re-center the ASD. We already know the middle plot was significant. We are going to watch the Time:Instructor.DRobot terms as we change the center point at ASD.C

Test -1 SD of ASD

• We move the center to be -1 SD by adding 1 SD

LongSim$ASD.N1sd<-LongSim$ASD.C+sd(LongSim$ASD.C)
Cov2.Model.Simple.N1sd<-lmer(Coordination ~ Time*Instructor.D*ASD.N1sd
                +(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Cov2.Model.Simple.N1sd, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time * Instructor.D * ASD.N1sd + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -127.7   -100.4     75.9   -151.7       60 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.25728 -0.53957 -0.00054  0.73048  1.68226 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev. Corr
##  Subject  (Intercept) 0.0005812 0.02411      
##           Time        0.0004871 0.02207  1.00
##  Residual             0.0047984 0.06927      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                                  Estimate Std. Error        df t value Pr(>|t|)
## (Intercept)                      0.404358   0.053652 25.063026   7.537 6.74e-08
## Time                             0.053680   0.026610 13.221798   2.017  0.06444
## Instructor.DRobot               -0.066083   0.059432 25.063026  -1.112  0.27673
## ASD.N1sd                        -0.097154   0.028438 25.063026  -3.416  0.00217
## Time:Instructor.DRobot           0.008433   0.029477 13.221798   0.286  0.77924
## Time:ASD.N1sd                   -0.009305   0.014105 13.221798  -0.660  0.52075
## Instructor.DRobot:ASD.N1sd       0.051776   0.034086 25.063026   1.519  0.14128
## Time:Instructor.DRobot:ASD.N1sd  0.036742   0.016906 13.221798   2.173  0.04849
##                                    
## (Intercept)                     ***
## Time                            .  
## Instructor.DRobot                  
## ASD.N1sd                        ** 
## Time:Instructor.DRobot             
## Time:ASD.N1sd                      
## Instructor.DRobot:ASD.N1sd         
## Time:Instructor.DRobot:ASD.N1sd *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Time:Instructor.DRobot is not significant. So the left panel is our graph is not an interaction

Test +1 SD of ASD

• We move the center to be +1 SD by subtracting 1 SD

LongSim$ASD.P1sd<-LongSim$ASD.C-sd(LongSim$ASD.C)
Cov2.Model.Simple.P1sd<-lmer(Coordination ~ Time*Instructor.D*ASD.P1sd
                +(1+Time|Subject), data=LongSim, REML=FALSE)
summary(Cov2.Model.Simple.P1sd, correlation=F)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Coordination ~ Time * Instructor.D * ASD.P1sd + (1 + Time | Subject)
##    Data: LongSim
## 
##      AIC      BIC   logLik deviance df.resid 
##   -127.7   -100.4     75.9   -151.7       60 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.25728 -0.53957 -0.00054  0.73048  1.68226 
## 
## Random effects:
##  Groups   Name        Variance  Std.Dev. Corr
##  Subject  (Intercept) 0.0005812 0.02411      
##           Time        0.0004871 0.02207  1.00
##  Residual             0.0047984 0.06927      
## Number of obs: 72, groups:  Subject, 12
## 
## Fixed effects:
##                                  Estimate Std. Error        df t value Pr(>|t|)
## (Intercept)                      0.177587   0.028836 25.063027   6.159 1.92e-06
## Time                             0.031961   0.014302 13.221798   2.235  0.04330
## Instructor.DRobot                0.054770   0.048776 25.063027   1.123  0.27213
## ASD.P1sd                        -0.097154   0.028438 25.063027  -3.416  0.00217
## Time:Instructor.DRobot           0.094195   0.024192 13.221798   3.894  0.00179
## Time:ASD.P1sd                   -0.009305   0.014105 13.221798  -0.660  0.52075
## Instructor.DRobot:ASD.P1sd       0.051776   0.034086 25.063027   1.519  0.14128
## Time:Instructor.DRobot:ASD.P1sd  0.036742   0.016906 13.221798   2.173  0.04849
##                                    
## (Intercept)                     ***
## Time                            *  
## Instructor.DRobot                  
## ASD.P1sd                        ** 
## Time:Instructor.DRobot          ** 
## Time:ASD.P1sd                      
## Instructor.DRobot:ASD.P1sd         
## Time:Instructor.DRobot:ASD.P1sd *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Time:Instructor.DRobot is significant (as it has to be). So the right panel in our graph is an interaction.
• In summary, our two way interaction changes as function of ASD score

References

Chlebowski, C., Green, J. A., Barton, M. L., & Fein, D. (2010). Using the childhood autism rating scale to diagnose autism spectrum disorders. Journal of autism and developmental disorders, 40(7), 787-799.

Srinivasan, S. M., Kaur, M., Park, I. K., Gifford, T. D., Marsh, K. L., & Bhat, A. N. (2015). The effects of rhythm and robotic interventions on the imitation/praxis, interpersonal synchrony, and motor performance of children with autism spectrum disorder (ASD): a pilot randomized controlled trial. Autism research and treatment.