Stepwise and Hierarchical

Making the intercept and slopes makes sense!

• When to use depends on your questions. However, centering is safest to do (and is often recommended)
  • Centering
  • Zscore
  • POMP
• You need to decide on whether it makes sense to transform both DV and IVs or one or the other.
• Let’s make a practice dataset to explore
• We will transform just the IVs for now:

library(car) #graph data
library(stargazer)
# IQ scores of 5 people
Y<-c(85, 90, 100, 120, 140)
# Likert scale rating of liking of reading books (1 hate to 7 love)
X1<-c(1,2,4,6,7)
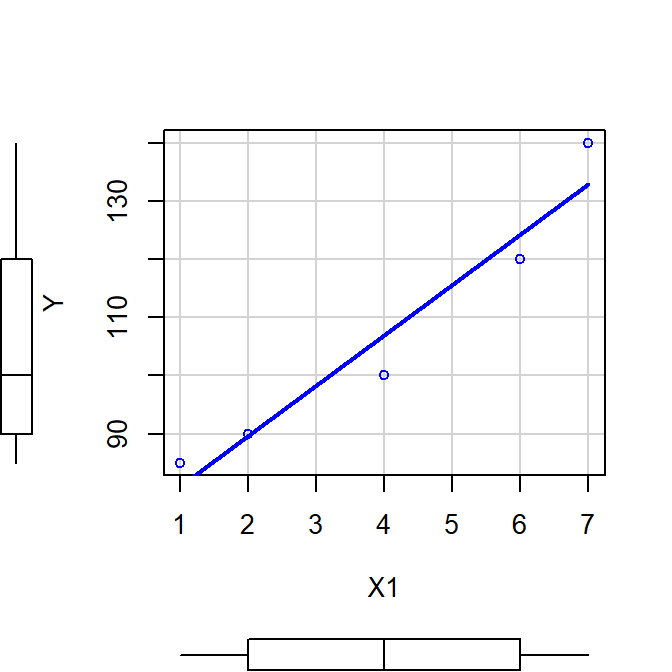
scatterplot(Y~X1, smooth=FALSE)
Mr<-lm(Y~X1)
stargazer(Mr,type="html",
          intercept.bottom = FALSE, notes.append = FALSE, header=FALSE)

	Dependent variable:
	Y
Constant	72.385***
	(6.010)
X1	8.654***
	(1.305)
Observations	5
R2	0.936
Adjusted R2	0.915
Residual Std. Error	6.655 (df = 3)
F Statistic	43.958*** (df = 1; 3)
Note:	p<0.1; p<0.05; p<0.01

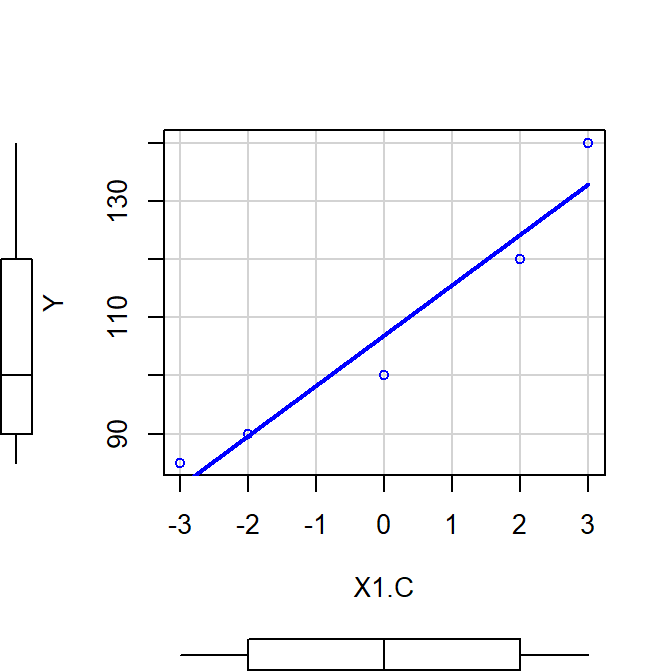
Center

• \(Center = {X - M}\)
• Intercept is not at the MEAN of IV (no 0 of IV)
• Does NOT changes meaning of slope
• R: scale(Data,scale=FALSE)[,]
  • scale add a dimension to our new variable, and we can remove it using [,]
    • We usually don’t need this, but it can mess up sometime down the road

X1.C<-scale(X1,scale=FALSE)[,]
scatterplot(Y~X1.C, smooth=FALSE)
Mc<-lm(Y~X1.C)
stargazer(Mc,type="html",
          intercept.bottom = FALSE, notes.append = FALSE, header=FALSE)

	Dependent variable:
	Y
Constant	107.000***
	(2.976)
X1.C	8.654***
	(1.305)
Observations	5
R2	0.936
Adjusted R2	0.915
Residual Std. Error	6.655 (df = 3)
F Statistic	43.958*** (df = 1; 3)
Note:	p<0.1; p<0.05; p<0.01

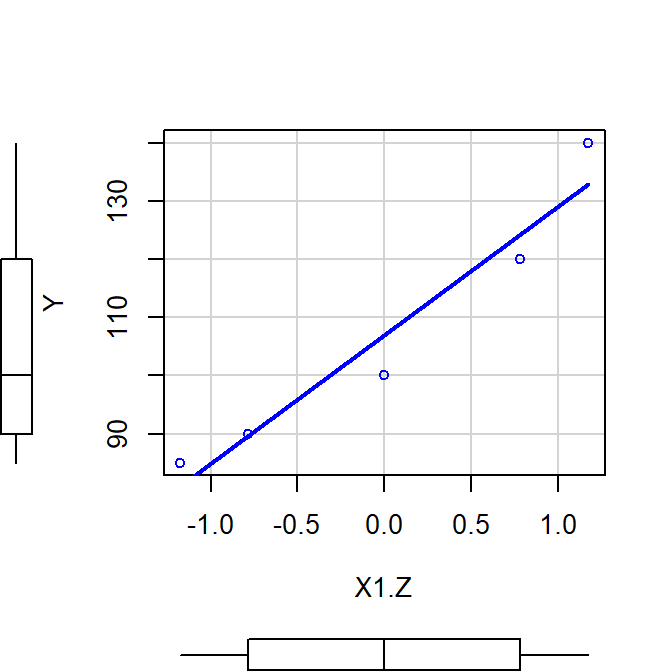
Zscore

• \(Z = \frac{X - M}{s}\)
• Intercept is not at the MEAN of IV (no 0 of IV)
• Slope changes meaning: no longer in unites of original DV, now in sd units
• R: scale(data)[,]

#Zscore
X1.Z<-scale(X1)[,] 
scatterplot(Y~X1.Z, smooth=FALSE)
Mz<-lm(Y~X1.Z)
stargazer(Mz,type="html",
          intercept.bottom = FALSE, notes.append = FALSE, header=FALSE)

	Dependent variable:
	Y
Constant	107.000***
	(2.976)
X1.Z	22.063***
	(3.328)
Observations	5
R2	0.936
Adjusted R2	0.915
Residual Std. Error	6.655 (df = 3)
F Statistic	43.958*** (df = 1; 3)
Note:	p<0.1; p<0.05; p<0.01

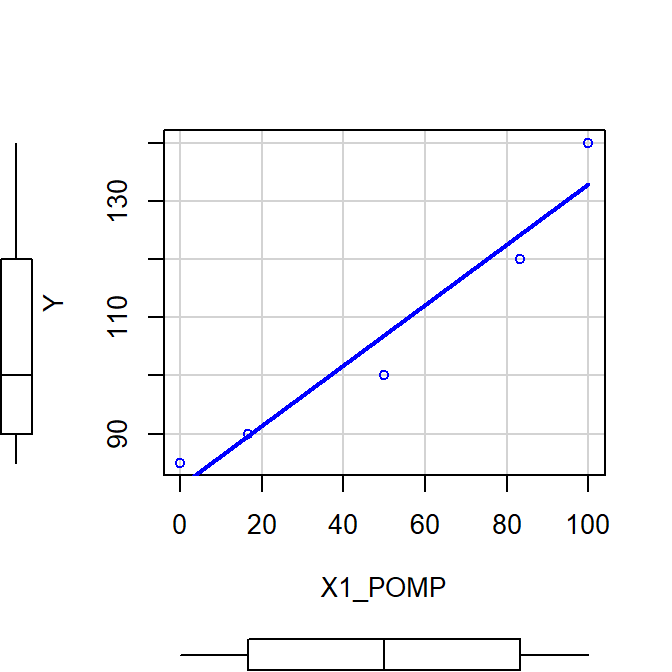
POMP

• \(POMP = \frac{X - MinX}{Max_X - Min_X}*100\)
• Note: I like to X 100 cause I find it easier to think in percent (not proportion)
• Useful when data are bounded (or scaled funny)
• Intercept is again at 0 of IV [but the slopes is different, so the intercept changes a bit]
• Does changes meaning of slope: is now a function of percent change of IV

X1_POMP = (X1 - min(X1)) / (max(X1) - min(X1))*100
scatterplot(Y~X1_POMP, smooth=FALSE)
Mp<-lm(Y~X1_POMP)
stargazer(Mp,type="html",
          intercept.bottom = FALSE, notes.append = FALSE, header=FALSE)

	Dependent variable:
	Y
Constant	81.038***
	(4.919)
X1_POMP	0.519***
	(0.078)
Observations	5
R2	0.936
Adjusted R2	0.915
Residual Std. Error	6.655 (df = 3)
F Statistic	43.958*** (df = 1; 3)
Note:	p<0.1; p<0.05; p<0.01

Simultaneous Regression (standard approach)

• Put all your variables in and see what the effect is of each term
• Very conservative approach
• Does not allow you to understand additive effects very easily
• You noticed this problem when we were trying to explain Health ~ Years married + Age
• Had you only looked at this final model you might never have understood that Years married acted as a good predictor on its own.
• Also what if you have a theory you want to test? You need to see the additive effects.

Hierarchical Modeling

• Is the change in \(R^2\), meaningful (Model 2 \(R^2\) - Model 1 \(R^2\))?
• The order in which models are run are meaningful
• Terms in models do not need to be analyzed one at a time, but can be entered as ‘sets’
• a set of variables are theoretically or experimentally driven
• So Model 2 \(R^2\) - Model 1 \(R^2\) meaningful?

Hierarchical Modeling driven by the researcher

• Forward selection: Start with simple models and get more complex nested models
• Backward selection: Start with complex nested models and get more simple
• Stepwise selection: can be viewed as a variation of the forward selection method (one predictor at a time) but predictors are deleted in subsequent steps if they no longer contribute appreciable unique prediction
• Which you choose is can depend on how you like to ask questions

Forward Selection of nested models

• A common approach “model building”
• Again let’s make up our dummy data

library(MASS) #create data
py1 =.6 #Cor between X1 (ice cream) and happiness
py2 =.4 #Cor between X2 (Brownies) and happiness
p12= .2 #Cor between X1 (ice cream) and X2 (Brownies)
Means.X1X2Y<- c(10,10,10) #set the means of X and Y variables
CovMatrix.X1X2Y <- matrix(c(1,p12,py1, p12,1,py2, py1,py2,1),3,3) # creates the covariate matrix 
set.seed(42)
CorrDataT<-mvrnorm(n=100, mu=Means.X1X2Y,Sigma=CovMatrix.X1X2Y, empirical=TRUE)
CorrDataT<-as.data.frame(CorrDataT)
colnames(CorrDataT) <- c("IceCream","Brownies","Happiness")

library(corrplot)
corrplot(cor(CorrDataT), method = "number")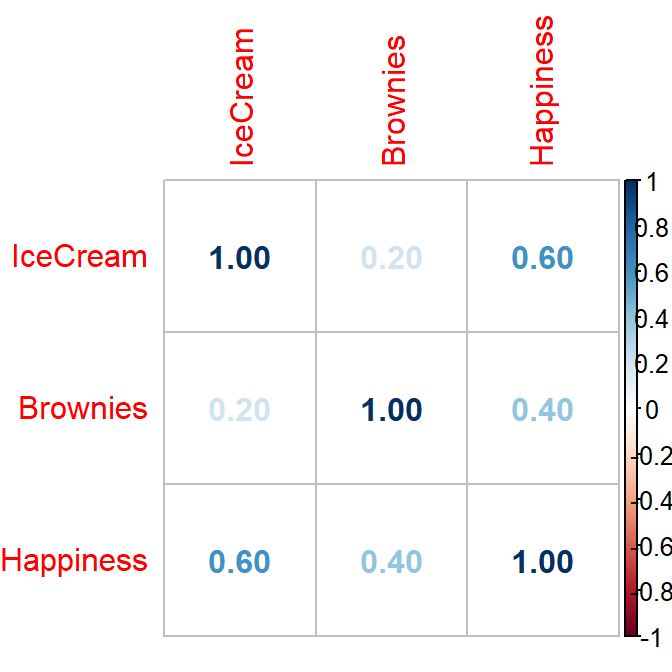

First alittle side track…

• Remember the \(R2\) values are reported as F values right?
• This means you can actually get an ANOVA like table for the model
• for example:

###############Model 1 
Ice.Model<-lm(Happiness~ IceCream, data = CorrDataT)
anova(Ice.Model)

## Analysis of Variance Table
## 
## Response: Happiness
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## IceCream   1  35.64  35.640  55.125 4.193e-11 ***
## Residuals 98  63.36   0.647                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• The \(R2\) this is explained to unexplained variance (like in our ANOVA)
• \(R^2 = \frac{SS_{explained}}{SS_{explained}+SS_{residual}}\)
• just to check: anova(Ice.Model) 64.36
• which matched the \(R^2\) that R gives us 0.36
• When we check to see which model is best we actually test the differences

Lets forward-fit our models

• Model 1 (Smaller model)

Ice.Model<-lm(Happiness~ IceCream, data = CorrDataT)
R2.Model.1<-summary(Ice.Model)$r.squared

• Model 2 (Larger model)

###############Model 1 
Ice.Brown.Model<-lm(Happiness~ IceCream+Brownies, data = CorrDataT)
R2.Model.2<-summary(Ice.Brown.Model)$r.squared

library(stargazer)
stargazer(Ice.Model,Ice.Brown.Model,type="html",
          column.labels = c("Model 1", "Model 2"),
          intercept.bottom = FALSE,
          single.row=FALSE, 
          star.cutoffs = c(0.1, 0.05, 0.01, 0.001),
          star.char = c("@", "*", "**", "***"), 
          notes= c("@p < .1 *p < .05 **p < .01 ***p < .001"),
          notes.append = FALSE, header=FALSE)

	Dependent variable:
	Happiness
	Model 1	Model 2
	(1)	(2)
Constant	4.000***	1.667@
	(0.812)	(0.982)
IceCream	0.600***	0.542***
	(0.081)	(0.077)
Brownies		0.292***
		(0.077)
Observations	100	100
R2	0.360	0.442
Adjusted R2	0.353	0.430
Residual Std. Error	0.804 (df = 98)	0.755 (df = 97)
F Statistic	55.125*** (df = 1; 98)	38.366*** (df = 2; 97)
Note:	@p < .1 p < .05 p < .01 p < .001

• Let’s the difference in \(R^2\)
  • \(R_{Change}^2\) =\(R_{Larger}^2\) - \(R_{Smaller}^2\)
• In R, we call for function anova and use an \(F\) where the degrees of freedom is the number of parameter differences between Larger and Smaller model

R2.Change<-R2.Model.2-R2.Model.1
anova(Ice.Model,Ice.Brown.Model)

## Analysis of Variance Table
## 
## Model 1: Happiness ~ IceCream
## Model 2: Happiness ~ IceCream + Brownies
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1     98 63.360                                  
## 2     97 55.275  1     8.085 14.188 0.0002838 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• The \(R_{Change}^2\) = 0.0816667 is significant
  
• So, in other words, we see model 2 fit the data better than model 1.

Backward-fitting of nested models

• You as does taking away variables reduce my \(R^2\) significantly
• Sometimes used to validate you have a parsimonious model
• You might forward-fit a set of variables and backward fit critical ones to test a specific hypothesis
• Using the same data as above, we will get the same values (just negative)
  • \(R_{Change}^2\) =\(R_{smaller}^2\) - \(R_{Larger}^2\)

###############Model 1.B 
Ice.Brown.Model<-lm(Happiness~ IceCream+Brownies, data = CorrDataT)
R2.Model.1.B<-summary(Ice.Brown.Model)$r.squared
###############Model 2.B
Ice.Model<-lm(Happiness~ IceCream, data = CorrDataT)
R2.Model.2.B<-summary(Ice.Model)$r.squared
R2.Change.B<-R2.Model.2.B-R2.Model.1.B
anova(Ice.Brown.Model,Ice.Model)

## Analysis of Variance Table
## 
## Model 1: Happiness ~ IceCream + Brownies
## Model 2: Happiness ~ IceCream
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1     97 55.275                                  
## 2     98 63.360 -1    -8.085 14.188 0.0002838 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• The \(R_{Change}^2\) = -0.0816667 is significant
  
• So, in other words, we see model 1 is a worse fit of the data than model 2

Stepwise modeling by Computer

• Stepwise with many predicts is often done by computer and it does not always assume nested models (you can add and remove at the same)
• Exploratory: you have too many predictors and have no idea where to start
• You give the computer a larger number of predictors, and the computer decides the best fit model
• Sounds good, right? No, as the results can be unstable
  • Change one variable in the set and the final model can change
  • High chance of type I and type II error
  • The computer makes decisions based on Akaike information criterion (AIC) not selected based on a change in \(R^2\), because models are not nested
  • also computer makes decisions purely on fit values and has nothing do with a theory
  • Solutions are often unique to that particular dataset
  • The best model is often the one that parses a theory and only a human can do that at present
• Not really publishable because of these problems

Parsing influence

• As models get bigger and bigger its becomes a challenge to figure out the unique contribution to \(R^2\) of each variable
• There are many computation solutions that you can select from, but we will use one called lmg
• you can read about all the different ones here: https://core.ac.uk/download/pdf/6305006.pdf
• these methods are not well known in psychology, but can be very useful when people ask you what the relative importance of each variable is
• two approaches: show absolute \(R^2\) for each term or the relative % of \(R^2\) for each term

library(relaimpo)
# In terms of R2
calc.relimp(Ice.Brown.Model) 

## Response variable: Happiness 
## Total response variance: 1 
## Analysis based on 100 observations 
## 
## 2 Regressors: 
## IceCream Brownies 
## Proportion of variance explained by model: 44.17%
## Metrics are not normalized (rela=FALSE). 
## 
## Relative importance metrics: 
## 
##                lmg
## IceCream 0.3208333
## Brownies 0.1208333
## 
## Average coefficients for different model sizes: 
## 
##           1X       2Xs
## IceCream 0.6 0.5416667
## Brownies 0.4 0.2916667

# as % of R2
calc.relimp(Ice.Brown.Model,rela = TRUE) 

## Response variable: Happiness 
## Total response variance: 1 
## Analysis based on 100 observations 
## 
## 2 Regressors: 
## IceCream Brownies 
## Proportion of variance explained by model: 44.17%
## Metrics are normalized to sum to 100% (rela=TRUE). 
## 
## Relative importance metrics: 
## 
##                lmg
## IceCream 0.7264151
## Brownies 0.2735849
## 
## Average coefficients for different model sizes: 
## 
##           1X       2Xs
## IceCream 0.6 0.5416667
## Brownies 0.4 0.2916667

Final notes:

• If you play with lots of predictors and do lots of models, something will be significant

• Type I error is a big problem because of the ‘researcher degree of freedom problem’

• Type II increases as a function of the number of predictors. a) you slice too much pie, b) each variable might try to each eat someone else’s slice

• Less is more: ask targeted questions with as orthogonal a set of variables as you can