Multi-Level Modeling: Two Levels

Multi-Level Models

• Hierarchical designs: Students nested in classrooms [Clustered data] with student-level predictors
  • We will examine the effect of adding level 1 random slopes first today
• Multilevel designs: Students nested in classrooms with student-level and classroom-level predictors
  • Examine random slopes of level 2 variables

Example

• Last week we found that active learning improved math scores. We replicate this study and expand into level 2 predictions and examine random slopes.
• You want to measure how students respond to a new type of active learning method (computer-based) in math class
• You measure students math scores (DV) and the proportion of time (IV) they spend using the computer (which you assign)
  • You expect that the more time they spend doing the active learning method, the higher their math test scores will be
• You also measure how supportive (control and/or moderator) each student feels the teacher is about this new method.
  • Also, maybe if the students feel the teacher approves of the new method, they might engage with it more
• You tell two the teachers that the active learning method works and the other two its experimental [Told level 2 variable]
  • You want to know if the teacher needs to believe the program works for it to have an effect
• You have access to different classrooms with 50 students per class
• Let’s go collect (simulate) our study.

Simulation

• Set the same slope of proportion of time (plus noise)
• Different intercept per class (plus noise) [which will implicitly correlate with supportive]
• Different slope per class on supportive (plus noise)
• Teachers in Classrooms 1 and 2 were Told the program works and 3 & 4 that it is experimental
• Set an interaction between proportion of time and supportive

#Set seed so your answers are all the same
set.seed(9)
# Sample Per class room people
n1 <- 50; n2 <- 50; n3 <- 50; n4 <- 50
N<-n1+n2+n3+n4 # Total N
# Uniform distrobution of ActiveTime per classroom
X1 <- runif(n1, 0, 1); X2 <- runif(n2, 0, 1)
X3 <- runif(n3, 0, 1); X4 <- runif(n4, 0, 1)
# Uniform distrobution of support per classroom
Z1 <- runif(n1, 0, 1); Z2 <- runif(n2, 0, 1)
Z3 <- runif(n3, 0, 1); Z4 <- runif(n4, 0, 1)
# Intercepts per classroom
B0.1 <- 80; B0.2 <- 75
B0.3 <- 65; B0.4 <- 68
# Same slope for ActiveTime per classroom + Noise
B1 <- rnorm(n1, 10, sd=2.5); B2 <- rnorm(n2, 10, sd=2.5)
B3 <- rnorm(n3, 10, sd=2.5); B4 <- rnorm(n4, 10, sd=2.5)
# different slope for support per classroom + Noise
g1 <- rnorm(n1, 10, sd=2.5); g2 <- rnorm(n2, 5, sd=2.5)
g3 <- rnorm(n3, -5, sd=2.5); g4 <- rnorm(n4, 2, sd=2.5)
# Same interaction between ActiveTime*support support per classroom + Noise
f1<- rnorm(n3, 15, sd=2.5); f2<- rnorm(n3, 15, sd=2.5)
f3<- rnorm(n3, 15, sd=2.5); f4<- rnorm(n3, 15, sd=2.5)
# noise per student within each classroom
e1 <- rnorm(n1, 0, sd=2.5); e2 <- rnorm(n2, 0, sd=2.5)
e3 <- rnorm(n3, 0, sd=2.5); e4 <- rnorm(n4, 0, sd=2.5)

# Our equation to  create Y for each classroom
Y1 = B1*scale(X1,scale=F)+g1*Z1+f1*scale(X1,scale=F)*scale(Z1,scale=F) + B0.1 + e1
Y2 = B2*scale(X2,scale=F)+g2*Z2+f2*scale(X2,scale=F)*scale(Z2,scale=F) + B0.2 + e2
Y3 = B3*scale(X3,scale=F)+g3*Z3+f3*scale(X3,scale=F)*scale(Z3,scale=F) + B0.3 + e3
Y4 = B4*scale(X4,scale=F)+g4*Z4+f4*scale(X4,scale=F)*scale(Z4,scale=F) + B0.4 + e4
# Merge classrooms into 1 data.frame
MLM.Data<-data.frame(Math=c(Y1,Y2,Y3,Y4),ActiveTime=c(X1,X2,X3,X4),Support=c(Z1,Z2,Z3,Z4),
                     Classroom=c(rep("C1",n1),rep("C2",n2),rep("C3",n3),rep("C4",n4)),
                     Told=c(rep("Works",n1),rep("Works",n2),
                               rep("Experimental",n3),rep("Experimental",n4)),
                     StudentID=as.factor(1:N))

Plot our Clusters

• Students nested in classrooms

library(ggplot2)
theme_set(theme_bw(base_size = 12, base_family = "")) 

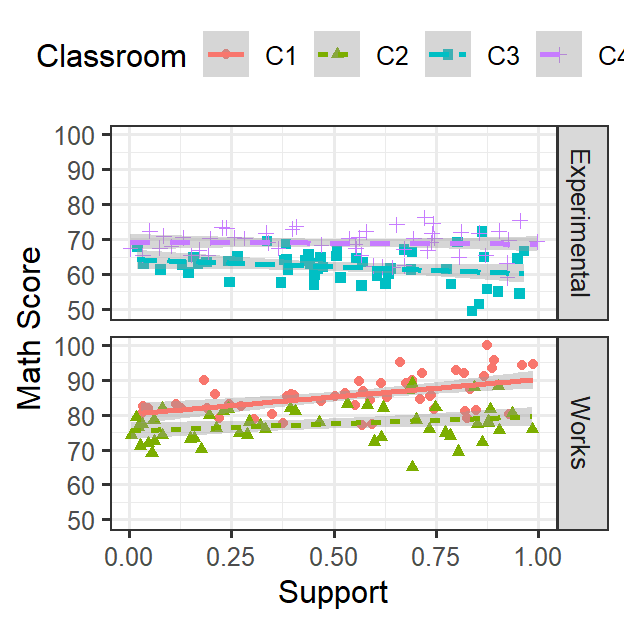
ClassRoom.Active <-ggplot(data = MLM.Data, aes(x = ActiveTime, y=Math,group=Classroom))+
  facet_grid(Told~.)+
  geom_point(aes(colour = Classroom,shape=Classroom))+
  geom_smooth(method = "lm", se = TRUE, aes(colour = Classroom, linetype=Classroom))+
  xlab("Active Learning Time")+ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Active

ClassRoom.Support <-ggplot(data = MLM.Data, aes(x = Support, y=Math,group=Classroom))+
 facet_grid(Told~.)+
  geom_point(aes(colour = Classroom, shape=Classroom))+
  geom_smooth(method = "lm", se = TRUE, aes(colour = Classroom,linetype=Classroom))+
  xlab("Support")+ylab("Math Score")+
  theme(legend.position = "top")
ClassRoom.Support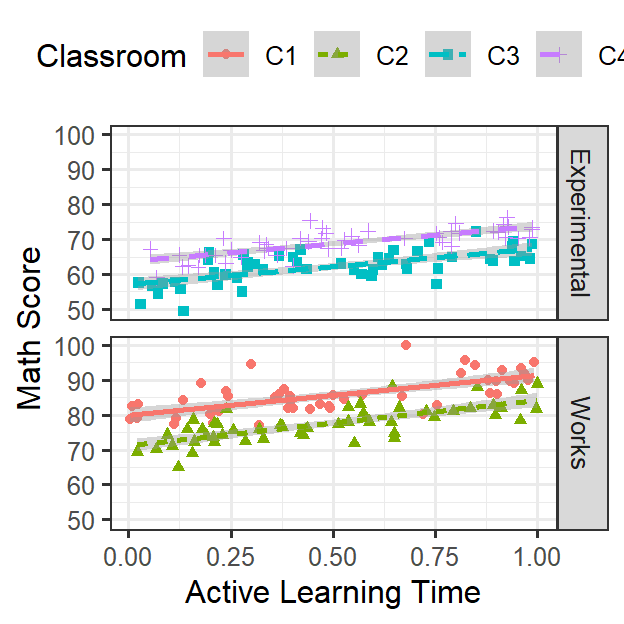

Random Intercepts & Random slopes

• Students are nested in their classroom
• Each classroom can have their own intercept [Random intercept] (like last week)
• As seen in the figure above, support each kid reported is not having a consistent effect on math score
  • This could be for many reasons (such as teachers attitude about active learning)
  • You are mainly interested in the effect of active learning, thus you want to control for support or look for moderation
    • In this case, support seems related to math score, but the effect clearly varies by classroom [Random slope]

Random Slopes of Level 1

• When you set a random slope you are saying that each classroom can have its own slope on that variable
  • You are trying to capture the noise around the population slope, given the multiple measurements of the classrooms (remember which are sort of conceptually repeated measures)
  • That “noise” could be systematic or unsystematic
• There are different perspectives about what should be allowed to be a random slope
  • It is clear that support slope varies as the function of the teacher (that might be systematic error that we want to control for, but in future studies, we could try to explain)
  • It is clear that Active Learning times does not really vary across classrooms

Equations

Level 1 remains the same as last week

Level 2 Intercept

\[B_{0j} = \gamma_{01}W_j+\gamma_{00}+u_{0j} \]

• Where \(W_j\) = predictor of level 2 (classroom)
• Where \(\gamma_{10}\) = new fixed effect on the level 2 predictor of the classroom
• Where \(\gamma_{00}\) = intercept of the classroom
• Where \(u_{0j}\) = random deviation of the classroom intercept from fixed population intercept
• We assume students will vary randomly around the population intercept of classroom

Level 2 Slope

\[B_{1j} = \gamma_{11}W_j+\gamma_{10}+u_{1j} \]

• Where \(W_j\) = predictor of level 2 (classroom)
• Where \(\gamma_{11}\) = new fixed effect on the level 2 predictor of the classroom
• Where \(\gamma_{10}\) = slope of the classroom
• Where \(u_{1j}\) = random deviation of the classroom slope from fixed population slope
• We assume students will vary randomly around the population intercept of classroom
• Note: We would repeat this for each level of classroom we have (g, etc)

Mixed Equation

• We put level 1 and level 2 together \[y_{ij} = (\gamma_{11}W_j+\gamma_{10}+u_{1j})X_{ij} + (\gamma_{01}W_j+\gamma_{00}+u_{0j})+ r_{ij} \]

lmer function

• Review: lmer(DV ~ IV +(1|RandomFactor), …)
  • (1|RandomFactor), means let the intercept of the random factor vary a function of the group (cluster).
  • In our case, (1|Classroom), means that we let each classroom have its own intercept
• Random Slope & Correlated Random intercept: lmer(DV ~ IV +(1+Control|RandomFactor), …)
  • We let each slope of the control variable vary as a function of the group
  • Also, it means we allow each intercept of each classroom correlates with the slope of the control
• Random Slope & Non-Correlated Random intercept: lmer(DV ~ IV +(1+Control||RandomFactor), …)
  • We let each slope of the control variable vary as a function of the group
  • Also, it means we block the intercept of each classroom with correlating with the slope of the control
• Random Slope & No Random intercept: lmer(DV ~ IV +(0+Control|RandomFactor), …)
  • We let each slope of the control variable vary as a function of the group
  • We block the model from calculating a random intercept
    • We would use this model if the random slope and intercept basically yielded the same information (\(r = 1\))

Analysis of Random Level 1 Slopes

• You need to decide about centering. Grand mean or Cluster mean and for both the IV and control
• Support was measured per student, so clearly, its level 1 right…but is it? The degree of support depends on which classroom they belonged too and maybe depends on what the teacher was told about the program (Level 2)
• Activity time in this experiment was assigned condition and does not depends on the classroom, it depends on the student
• However, might how the student response to activity level (level 1) depend on (or be related to) the degree of support, maybe! Let’s find out.

Null Model

• No fixed factors (intercept only)

library(lme4)     #mixed model package by Douglas Bates et al
Model.Null<-lmer(Math ~1+(1|Classroom),  
                   data=MLM.Data, REML=FALSE)
summary(Model.Null)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ 1 + (1 | Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1222.3   1232.2   -608.2   1216.3      197 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.66017 -0.69735  0.00735  0.68158  2.99470 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 78.44    8.857   
##  Residual              23.13    4.809   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##             Estimate Std. Error     df t value Pr(>|t|)    
## (Intercept)   73.551      4.441  4.000   16.56 7.79e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Look at ICC: The var and sd of these values are what was seen in the table above

ICC.Model<-function(Model.Name) {
  tau.Null<-as.numeric(lapply(summary(Model.Name)$varcor, diag))
  sigma.Null <- as.numeric(attr(summary(Model.Name)$varcor, "sc")^2)
  ICC.Null <- tau.Null/(tau.Null+sigma.Null)
  return(ICC.Null)
}

• \(ICC = \frac{\tau}{\tau + \sigma^2}\), where \(\tau\) = 78.443 & \(\sigma^2\) = 23.129
• The ICC = 0.7722889 > 0, meaning we were correct to think of this as MLM problem

Forward-Fitted Modeling Approach

• We want to understand how the models fit the data we will add them in such a way to make sense of our questions and to ensure our model fits
  • We might not report all these models in a paper, but this process is helpful to understand

Add Random Intercepts

• We have to decide on centering for active learning time.
  • Given it looks fairly stable across classrooms and we want to be able to talk about its as general effect, lets grand mean center it

MLM.Data$ActiveTime.GM<-scale(MLM.Data$ActiveTime,scale=F)

Model.1<-lmer(Math ~ActiveTime.GM+(1|Classroom),  
                   data=MLM.Data, REML=FALSE)
summary(Model.1)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM + (1 | Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1091.1   1104.3   -541.6   1083.1      196 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.5503 -0.6569 -0.0730  0.6226  3.6403 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 78.82    8.878   
##  Residual              11.72    3.423   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##               Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)    73.5514     4.4455   4.0000   16.55 7.82e-05 ***
## ActiveTime.GM  11.2642     0.8154 196.0050   13.81  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr)
## ActiveTm.GM 0.000

• Our intercept was 73.55, which was significant
• Our slope was 11.26, which was significant
• Was this a better fit than the null model? Yes! (see below)

anova(Model.Null,Model.1)

## Data: MLM.Data
## Models:
## Model.Null: Math ~ 1 + (1 | Classroom)
## Model.1: Math ~ ActiveTime.GM + (1 | Classroom)
##            npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## Model.Null    3 1222.3 1232.2 -608.17   1216.3                         
## Model.1       4 1091.1 1104.3 -541.55   1083.1 133.24  1  < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Add Fixed Effects of Control

• We have to decide about centering
  • If we center relative the cluster it will mean the degree of support each student felt relative to their teacher.
  • If we center to the grand average it will mean the degree of support each student felt relative to each other.
• Lets go with cluster centering

library(plyr)
# Cluster mean
MLM.Data<-ddply(MLM.Data,.(Classroom), mutate, ClassSupport = mean(Support))
MLM.Data$Support.CC<-MLM.Data$Support-MLM.Data$ClassSupport

• Only add fixed effect of support

Model.2<-lmer(Math ~ ActiveTime.GM+Support.CC+(1|Classroom),  
              data=MLM.Data, REML=FALSE)
summary(Model.2)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM + Support.CC + (1 | Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1078.6   1095.1   -534.3   1068.6      195 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9376 -0.6003  0.0133  0.5959  3.4624 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 78.84    8.879   
##  Residual              10.88    3.299   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##               Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)    73.5514     4.4456   4.0000   16.55 7.82e-05 ***
## ActiveTime.GM  11.4325     0.7870 196.0046   14.53  < 2e-16 ***
## Support.CC      3.1650     0.8157 196.0000    3.88 0.000143 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM
## ActiveTm.GM 0.000        
## Support.CC  0.000  0.055

• Our intercept was 73.55, which was significant
• Our active slope was 11.43, which was significant
• Our support slope was 3.17, which was significant
• Was this a better fit than the model 1? Yes! (see below)

anova(Model.1,Model.2)

## Data: MLM.Data
## Models:
## Model.1: Math ~ ActiveTime.GM + (1 | Classroom)
## Model.2: Math ~ ActiveTime.GM + Support.CC + (1 | Classroom)
##         npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## Model.1    4 1091.1 1104.3 -541.55   1083.1                         
## Model.2    5 1078.6 1095.1 -534.30   1068.6 14.504  1  0.0001399 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Add Level 1 Random Slopes of Control

• But wait, support seemed to vary as a function of the class. We need to add the random slope of support

Model.3<-lmer(Math ~ ActiveTime.GM+Support.CC+(1+Support.CC|Classroom),  
              data=MLM.Data, REML=FALSE)
summary(Model.3)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC | Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1064.3   1087.4   -525.2   1050.3      193 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0342 -0.7269  0.0562  0.5989  3.1819 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev. Corr
##  Classroom (Intercept) 78.85    8.880        
##            Support.CC  13.27    3.643    1.00
##  Residual               9.91    3.148        
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##               Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)    73.5514     4.4454   4.0002  16.546 7.81e-05 ***
## ActiveTime.GM  10.9855     0.7514 196.0033  14.619  < 2e-16 ***
## Support.CC      2.9583     1.9811   3.9466   1.493    0.211    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM
## ActiveTm.GM 0.000        
## Support.CC  0.918  0.021 
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Our intercept was 73.55, which was significant
• Our active slope was 10.99, which was significant
• Our support slope was 2.96, which was NOT significant
  • Why did the fixed effect for support change?
• Was this a better fit than the model 2? Yes! (see below)

anova(Model.2,Model.3)

## Data: MLM.Data
## Models:
## Model.2: Math ~ ActiveTime.GM + Support.CC + (1 | Classroom)
## Model.3: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC | Classroom)
##         npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## Model.2    5 1078.6 1095.1 -534.30   1068.6                         
## Model.3    7 1064.3 1087.4 -525.15   1050.3 18.301  2  0.0001062 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Random Slopes

• Notice the correlation between random slope and the intercep (its 1)
  
• We can block it [(1+Support.CC||Classroom) OR USE (1|Classroom) + (0+Support.CC|Classroom))]

Model.3a<-lmer(Math ~ ActiveTime.GM+Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data, REML=FALSE)
summary(Model.3a)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC || Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1071.8   1091.6   -529.9   1059.8      194 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0272 -0.7003  0.0172  0.5958  3.3308 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 78.85    8.880   
##  Classroom.1 Support.CC  10.69    3.269   
##  Residual                10.06    3.171   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##               Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)    73.5514     4.4454   4.0001  16.545 7.81e-05 ***
## ActiveTime.GM  11.1567     0.7662 194.0181  14.560  < 2e-16 ***
## Support.CC      2.8910     1.8165   3.8582   1.591    0.189    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM
## ActiveTm.GM 0.000        
## Support.CC  0.000  0.020

• Does this change the fit?
• Note below that that 3 is a better fit than 3a,
  • But Model 3 voilated the assumption. So we move on with Model 3a

anova(Model.3,Model.3a)

## Data: MLM.Data
## Models:
## Model.3a: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC || Classroom)
## Model.3: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC | Classroom)
##          npar    AIC    BIC  logLik deviance Chisq Df Pr(>Chisq)   
## Model.3a    6 1071.8 1091.6 -529.90   1059.8                       
## Model.3     7 1064.3 1087.4 -525.15   1050.3 9.491  1   0.002065 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Lets finally test the level 1 and 2 interaction

Model.4<-lmer(Math ~ ActiveTime.GM*Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data, REML=FALSE)
summary(Model.4)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1055.0   1078.1   -520.5   1041.0      193 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9810 -0.6582 -0.0185  0.5562  3.3230 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 76.629   8.754   
##  Classroom.1 Support.CC  13.796   3.714   
##  Residual                 9.087   3.014   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                          Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)               73.6073     4.3821   3.9997  16.797 7.37e-05 ***
## ActiveTime.GM             11.0667     0.7291 193.5746  15.178  < 2e-16 ***
## Support.CC                 3.0609     2.0048   3.9023   1.527    0.203    
## ActiveTime.GM:Support.CC  11.9355     2.6768 192.8449   4.459 1.40e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Spp.CC
## ActiveTm.GM  0.000              
## Support.CC   0.000  0.017       
## AcT.GM:S.CC  0.003 -0.022  0.021

• Our intercept was 73.61, which was significant
• Our active slope was 11.07, which was significant
• Our support slope was 3.06, which was NOT significant
• Our interaction was 3.06, which was significant
• Was this a better fit than the model 3a? Yes! (see below)

anova(Model.3a,Model.4)

## Data: MLM.Data
## Models:
## Model.3a: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC || Classroom)
## Model.4: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
##          npar    AIC    BIC logLik deviance  Chisq Df Pr(>Chisq)    
## Model.3a    6 1071.8 1091.6 -529.9   1059.8                         
## Model.4     7 1055.0 1078.1 -520.5   1041.0 18.792  1  1.458e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Plot the final model

• We will plot in the traditional way
  • Support (-1SD, Mean, +SD)

library(effects)
# Set levels of support
SLevels<-c(mean(MLM.Data$Support.CC)-sd(MLM.Data$Support.CC),
                               mean(MLM.Data$Support.CC),
           mean(MLM.Data$Support.CC)+sd(MLM.Data$Support.CC))
#extract fixed effects
Results.Model.4<-Effect(c("ActiveTime.GM","Support.CC"),Model.4,
     xlevels=list(ActiveTime.GM=seq(-.5,.5,.2), 
                  Support.CC=SLevels))
#Convert to data frame for ggplot
Results.Model.4<-as.data.frame(Results.Model.4)
#Label Support for graphing
Results.Model.4$Support.F<-factor(Results.Model.4$Support.CC,
                        levels=SLevels,
                         labels=c("Low Support", "Mean Support", "High Support"))

#Plot fixed effect
Final.Fixed.Plot.1 <-ggplot(data = Results.Model.4, 
                            aes(x = ActiveTime.GM, y =fit, group=Support.F))+
  geom_line(size=2, aes(color=Support.F,linetype=Support.F))+
  coord_cartesian(xlim = c(-.5, .5),ylim = c(50, 90))+ 
  geom_ribbon(aes(ymin=fit-se, ymax=fit+se, group=Support.F, fill=Support.F),alpha=.2)+
  xlab("Proportion of Time Engaged in Active Learning \nCentered")+
  ylab("Math Score")+ 
  theme(legend.position = "top", 
        legend.title=element_blank())
Final.Fixed.Plot.1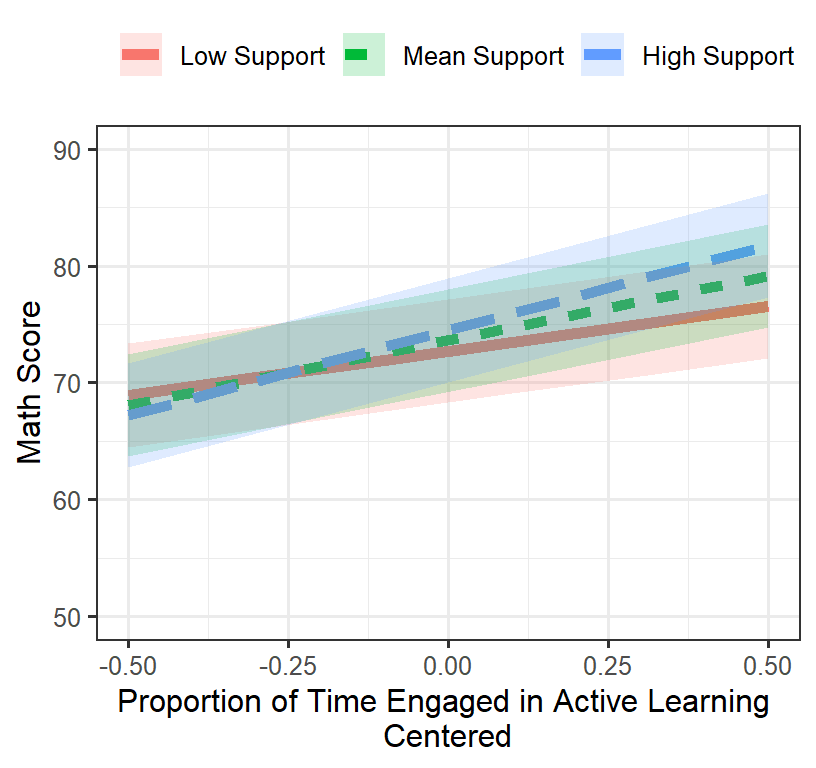

Format Output

library(texreg)
texreg(list(Model.1,Model.2,Model.3a,Model.4), 
       table = FALSE, use.packages = FALSE,
       single.row = FALSE, stars = c(0.001, 0.01, 0.05,0.1),digits=3)

Save the results of modeling

• This lets you make a Doc file

htmlreg(list(Model.1,Model.2,Model.3a,Model.4),file = "ModelResults.doc", 
        single.row = FALSE, stars = c(0.001, 0.01, 0.05,0.1),digits=3,
        inline.css = FALSE, doctype = TRUE, html.tag = TRUE, 
        head.tag = TRUE, body.tag = TRUE)

Re-Examine Random Effects

• Why don’t we let ActiveTime vary as a function of the classroom.
  • There is of course unsystematic error (noise) that we could account for

Model.5<-lmer(Math ~ ActiveTime.GM*Support.CC+(1+ActiveTime.GM+Support.CC||Classroom),  
              data=MLM.Data, REML=FALSE)
summary(Model.5)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## Math ~ ActiveTime.GM * Support.CC + (1 + ActiveTime.GM + Support.CC ||  
##     Classroom)
##    Data: MLM.Data
## 
##      AIC      BIC   logLik deviance df.resid 
##   1056.7   1083.1   -520.3   1040.7      192 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.8928 -0.6345  0.0072  0.5731  3.3479 
## 
## Random effects:
##  Groups      Name          Variance Std.Dev.
##  Classroom   (Intercept)   76.7011  8.7579  
##  Classroom.1 ActiveTime.GM  0.9878  0.9939  
##  Classroom.2 Support.CC    14.5540  3.8150  
##  Residual                   8.9915  2.9986  
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                          Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)               73.6159     4.3841   3.9997  16.792 7.38e-05 ***
## ActiveTime.GM             11.0832     0.8797   3.8113  12.599 0.000302 ***
## Support.CC                 3.1048     2.0516   3.8739   1.513 0.207008    
## ActiveTime.GM:Support.CC  12.0019     2.6642 188.7441   4.505 1.16e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Spp.CC
## ActiveTm.GM  0.000              
## Support.CC   0.000  0.015       
## AcT.GM:S.CC  0.003 -0.017  0.021

• We added alot of degrees of freedom to this model (more random slopes and more correlation between the terms)
• Will this improve the fit? In this case, NO! So adding the extra terms does not really help

anova(Model.4,Model.5)

## Data: MLM.Data
## Models:
## Model.4: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
## Model.5: Math ~ ActiveTime.GM * Support.CC + (1 + ActiveTime.GM + Support.CC || Classroom)
##         npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)
## Model.4    7 1055.0 1078.1 -520.50   1041.0                     
## Model.5    8 1056.7 1083.1 -520.35   1040.7 0.3082  1     0.5788

• We added alot of degrees of freedom to this model (more random slopes and more correlation between the terms)

Simulation Take 2

• Set the different slope of proportion of time (plus noise)
• Different intercept per class (plus noise) [which will implicitly correlate with supportive]
• Different slope per class on supportive (plus noise)
• Set same interaction between proportion of time and supportive
• Teachers in Classrooms 1 and 2 were Told the program works and 3 & 4 that it is experimental

#Set seed so your answers are all the same
set.seed(9)
# Sample Per class room people
n1 <- 50; n2 <- 50; n3 <- 50; n4 <- 50
N<-n1+n2+n3+n4 # Total N
# Uniform distrobution of ActiveTime per classroom
X1 <- runif(n1, 0, 1); X2 <- runif(n2, 0, 1)
X3 <- runif(n3, 0, 1); X4 <- runif(n4, 0, 1)
# Uniform distrobution of support per classroom
Z1 <- runif(n1, 0, 1); Z2 <- runif(n2, 0, 1)
Z3 <- runif(n3, 0, 1); Z4 <- runif(n4, 0, 1)
# Intercepts per classroom
B0.1 <- 80; B0.2 <- 75
B0.3 <- 65; B0.4 <- 68
# Same slope for ActiveTime per classroom + Noise
B1 <- rnorm(n1, 17, sd=2.5); B2 <- rnorm(n2, 12, sd=2.5)
B3 <- rnorm(n3, 8, sd=2.5); B4 <- rnorm(n4, 4, sd=2.5)
# different slope for support per classroom + Noise
g1 <- rnorm(n1, 10, sd=2.5); g2 <- rnorm(n2, 5, sd=2.5)
g3 <- rnorm(n3, -5, sd=2.5); g4 <- rnorm(n4, 2, sd=2.5)
# Same interaction between ActiveTime*support support per classroom + Noise
f1<- rnorm(n3, 15, sd=2.5); f2<- rnorm(n3, 15, sd=2.5)
f3<- rnorm(n3, 15, sd=2.5); f4<- rnorm(n3, 15, sd=2.5)
# noise per student within each classroom
e1 <- rnorm(n1, 0, sd=2.5); e2 <- rnorm(n2, 0, sd=2.5)
e3 <- rnorm(n3, 0, sd=2.5); e4 <- rnorm(n4, 0, sd=2.5)

# Our equation to  create Y for each classroom
Y1 = B1*scale(X1,scale=F)+g1*Z1+f1*scale(X1,scale=F)*scale(Z1,scale=F) + B0.1 + e1
Y2 = B2*scale(X2,scale=F)+g2*Z2+f2*scale(X2,scale=F)*scale(Z2,scale=F) + B0.2 + e2
Y3 = B3*scale(X3,scale=F)+g3*Z3+f3*scale(X3,scale=F)*scale(Z3,scale=F) + B0.3 + e3
Y4 = B4*scale(X4,scale=F)+g4*Z4+f4*scale(X4,scale=F)*scale(Z4,scale=F) + B0.4 + e4
# Merge classrooms into 1 data.frame
MLM.Data.2<-data.frame(Math=c(Y1,Y2,Y3,Y4),ActiveTime=c(X1,X2,X3,X4),Support=c(Z1,Z2,Z3,Z4),
                     Classroom=c(rep("C1",n1),rep("C2",n2),rep("C3",n3),rep("C4",n4)),
                     Told=c(rep("Works",n1),rep("Works",n2),
                               rep("Experimental",n3),rep("Experimental",n4)),
                     StudentID=as.factor(1:N))

Plot our Clusters

• Students nested in classrooms

library(ggplot2)
theme_set(theme_bw(base_size = 12, base_family = "")) 

ClassRoom.Active.2 <-ggplot(data = MLM.Data.2, aes(x = ActiveTime, y=Math,group=Classroom))+
  facet_grid(Told~.)+
  geom_point(aes(colour = Classroom))+
  geom_smooth(method = "lm", se = TRUE, aes(colour = Classroom))+
  xlab("Active Learning Time")+ylab("Math Score")+
  theme(legend.position = "none")
ClassRoom.Active.2

ClassRoom.Support.2 <-ggplot(data = MLM.Data.2, aes(x = Support, y=Math,group=Classroom))+
  facet_grid(Told~.)+
  geom_point(aes(colour = Classroom))+
  geom_smooth(method = "lm", se = TRUE, aes(colour = Classroom))+
  xlab("Support")+ylab("Math Score")+
  theme(legend.position = "none")
ClassRoom.Support.2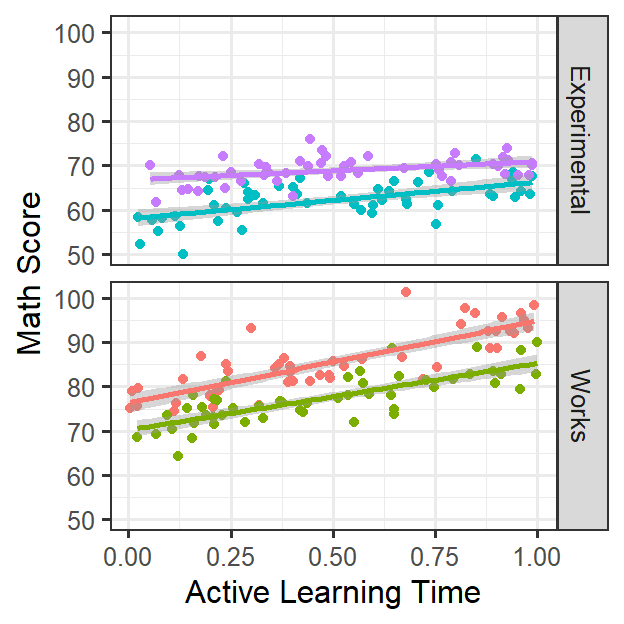

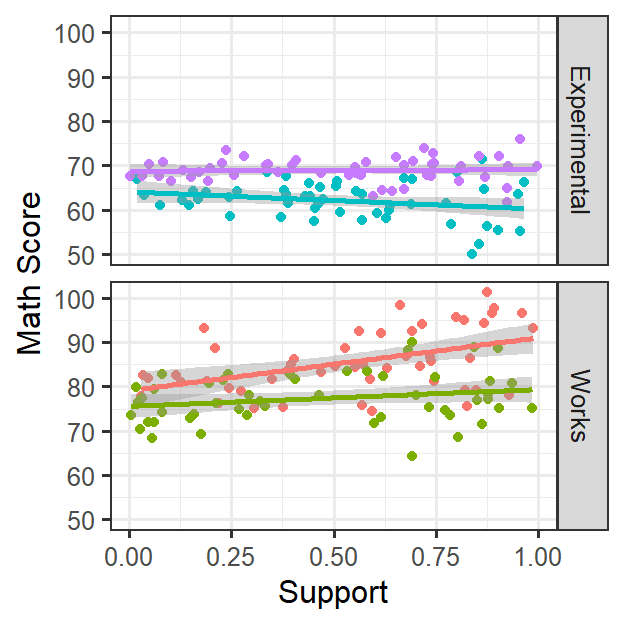
• Lets center the data just as before and do the modeling alittle faster, also lets just layer the random effects.
• As we add more random effects, watch what happens to the SE for each term

Random Intercept

MLM.Data.2$ActiveTime.GM<-scale(MLM.Data.2$ActiveTime,scale=F)
MLM.Data.2<-ddply(MLM.Data.2,.(Classroom), mutate, ClassSupport = mean(Support))
MLM.Data.2$Support.CC<-MLM.Data.2$Support-MLM.Data.2$ClassSupport

MLM.Model.1<-lmer(Math ~ ActiveTime.GM*Support.CC+(1|Classroom),  
              data=MLM.Data.2, REML=FALSE)

Random Slope & Intercept

MLM.Model.2<-lmer(Math ~ ActiveTime.GM*Support.CC+(1+Support.CC|Classroom),  
              data=MLM.Data.2, REML=FALSE)

Random Slopes & Intercept

MLM.Model.3<-lmer(Math ~ ActiveTime.GM*Support.CC+(1+ActiveTime.GM+Support.CC|Classroom),  
              data=MLM.Data.2, REML=FALSE)

• See the change in SE
  • Helps protect out type I error rate

library(texreg)
texreg(list(MLM.Model.1,MLM.Model.2,MLM.Model.3), 
       table = FALSE, use.packages = FALSE,
       single.row = FALSE, stars = c(0.001, 0.01, 0.05,0.1),digits=3)

Model fits

• In this case adding the L1 slope as random improved the fit

anova(MLM.Model.1,MLM.Model.2,MLM.Model.3)

## Data: MLM.Data.2
## Models:
## MLM.Model.1: Math ~ ActiveTime.GM * Support.CC + (1 | Classroom)
## MLM.Model.2: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC | Classroom)
## MLM.Model.3: Math ~ ActiveTime.GM * Support.CC + (1 + ActiveTime.GM + Support.CC | Classroom)
##             npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## MLM.Model.1    6 1105.8 1125.6 -546.91   1093.8                         
## MLM.Model.2    8 1088.0 1114.4 -535.98   1072.0 21.848  2  1.802e-05 ***
## MLM.Model.3   11 1056.8 1093.0 -517.38   1034.8 37.205  3  4.165e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Plot the final model

• We will plot in the traditional way
  • Support (-1SD, Mean, +SD)

# Set levels of support
SLevels.2<-c(mean(MLM.Data.2$Support.CC)-sd(MLM.Data.2$Support.CC),
                               mean(MLM.Data.2$Support.CC),
           mean(MLM.Data.2$Support.CC)+sd(MLM.Data.2$Support.CC))
Results.MLM.Model.3<-Effect(c("ActiveTime.GM","Support.CC"),MLM.Model.3,
     xlevels=list(ActiveTime.GM=seq(-.5,.5,.2), 
                  Support.CC=SLevels.2))
Results.MLM.Model.3<-as.data.frame(Results.MLM.Model.3)
Results.MLM.Model.3$Support.F<-factor(Results.MLM.Model.3$Support.CC,
                        levels=SLevels.2,
                         labels=c("Low Support", "Mean Support", "High Support"))
Final.Fixed.Plot.2 <-ggplot(data = Results.MLM.Model.3, 
                            aes(x = ActiveTime.GM, y =fit, group=Support.F))+
  geom_line(size=2, aes(color=Support.F,linetype=Support.F))+
  coord_cartesian(xlim = c(-.5, .5),ylim = c(50, 90))+ 
  geom_ribbon(aes(ymin=fit-se, ymax=fit+se, group=Support.F, fill=Support.F),alpha=.2)+
  xlab("Proportion of Time Engaged in Active Learning \nCentered")+
  ylab("Math Score")+ 
  theme(legend.position = "top", 
        legend.title=element_blank())
Final.Fixed.Plot.2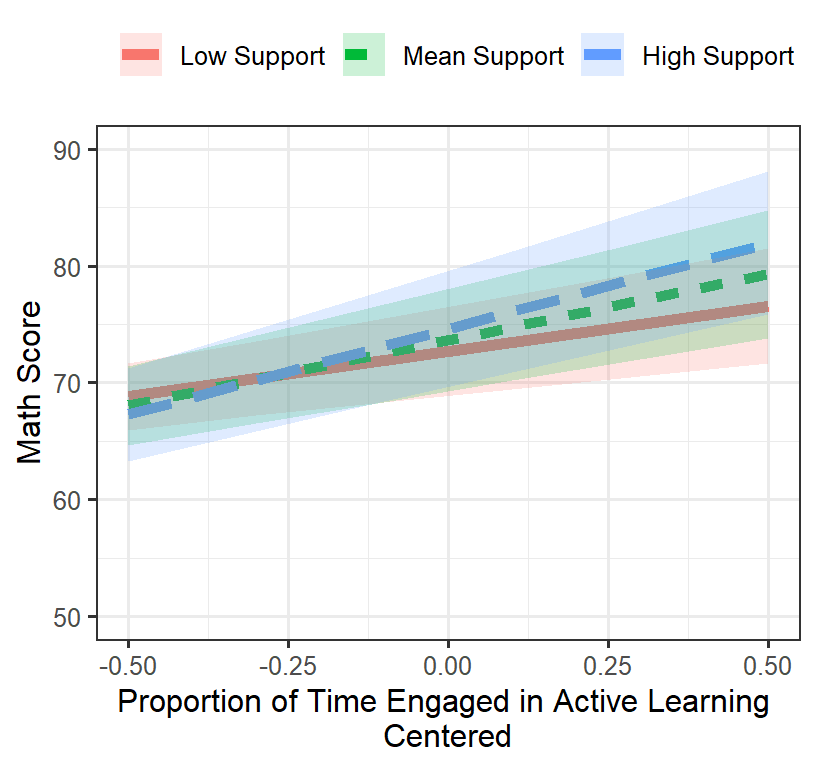

Multi-Level Model with Cross-level Interactions

• So far we examined the level 1 slopes, but there is Level 2 variable to deal with: what the teacher was told about the program
• The problem is going to be that teachers are nested in their classrooms, so we have implicitly controlled for the intercept differences for the Told variable
  • [Note: Told has 2 measurements we will not treat it as random]
• Lets go back to simulation 1 and re-examine the results given this Level 2 factor
• First lets make the variable numeric and center it.

MLM.Data.2$Told.N<-as.numeric(as.factor(MLM.Data.2$Told))
MLM.Data.2$Told.C<-scale(MLM.Data.2$Told.N,scale=F)[,]

Add Level 2 Fixed Effects

• Let’s start by working from Model 1 and add the Level 2

library(lme4)
L2test.1<-lmer(Math ~ ActiveTime.GM+Told.C
               +(1|Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.1)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM + Told.C + (1 | Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1127.7   1144.2   -558.9   1117.7      195 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.3473 -0.7294 -0.0060  0.6084  3.5710 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 12.91    3.593   
##  Residual              14.50    3.808   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##               Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)    73.5514     1.8164   3.9994  40.493 2.23e-06 ***
## ActiveTime.GM  11.8418     0.9071 196.0286  13.054  < 2e-16 ***
## Told.C         16.2312     3.6328   3.9996   4.468   0.0111 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM
## ActiveTm.GM 0.000        
## Told.C      0.000  0.004

• Our intercept was 73.55, which was significant
• Our active slope was 11.84, which was significant
• Our teacher slope was 16.23, which was significant
• Was this a better fit than the model 1? Yes! (see below)

anova(MLM.Model.1,L2test.1)

## Data: MLM.Data.2
## Models:
## L2test.1: Math ~ ActiveTime.GM + Told.C + (1 | Classroom)
## MLM.Model.1: Math ~ ActiveTime.GM * Support.CC + (1 | Classroom)
##             npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## L2test.1       5 1127.7 1144.2 -558.86   1117.7                         
## MLM.Model.1    6 1105.8 1125.6 -546.91   1093.8 23.907  1  1.011e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Add Cross-Level Interactions

L2test.2<-lmer(Math ~ ActiveTime.GM*Told.C+(1|Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.2)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Told.C + (1 | Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1091.4   1111.2   -539.7   1079.4      194 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.8458 -0.6170 -0.1151  0.6326  3.6811 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 12.88    3.589   
##  Residual              11.93    3.454   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)           73.5986     1.8108   3.9996  40.643 2.19e-06 ***
## ActiveTime.GM         11.6254     0.8233 196.0235  14.120  < 2e-16 ***
## Told.C                16.2274     3.6217   3.9996   4.481    0.011 *  
## ActiveTime.GM:Told.C  10.7132     1.6467 196.0235   6.506 6.29e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Told.C
## ActiveTm.GM  0.000              
## Told.C       0.000  0.004       
## ActT.GM:T.C  0.004 -0.040  0.000

• Our intercept was 73.6, which was significant
• Our active slope was 11.63, which was significant
• Our teacher slope was 16.23, which was significant
• Our interaction slope was 10.71, which was significant
• Was this a better fit than the L2test.1? No! (see below)

anova(L2test.1,L2test.2)

## Data: MLM.Data.2
## Models:
## L2test.1: Math ~ ActiveTime.GM + Told.C + (1 | Classroom)
## L2test.2: Math ~ ActiveTime.GM * Told.C + (1 | Classroom)
##          npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## L2test.1    5 1127.7 1144.2 -558.86   1117.7                         
## L2test.2    6 1091.4 1111.2 -539.70   1079.4 38.328  1   5.98e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Adding Back Support

• We know from the figures and previous models that support was an important variable
• What Support and told in the same model as Told we are going to have a problem because we can see in figures it is basically confounded

L2test.3<-lmer(Math ~ ActiveTime.GM*Told.C+Support.CC+(1+Support.CC|Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.3)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Told.C + Support.CC + (1 + Support.CC |  
##     Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1065.8   1095.5   -523.9   1047.8      191 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9037 -0.6303 -0.0269  0.5935  3.2055 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev. Corr
##  Classroom (Intercept) 49.802   7.057        
##            Support.CC  15.402   3.924    1.00
##  Residual               9.875   3.142        
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)           73.5960     3.5355   2.5652  20.816 0.000625 ***
## ActiveTime.GM         11.3120     0.7543 194.0727  14.997  < 2e-16 ***
## Told.C                 4.0842     2.6563   5.7194   1.538 0.177460    
## Support.CC             3.1934     2.1128   3.9054   1.511 0.206885    
## ActiveTime.GM:Told.C  10.1190     1.5091 193.8334   6.705 2.14e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Told.C Spp.CC
## ActiveTm.GM  0.000                     
## Told.C       0.000  0.094              
## Support.CC   0.927  0.024  0.031       
## ActT.GM:T.C  0.002 -0.048 -0.061 -0.036
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Our random slopes are correlated at 1 with the random intercept. That makes sense given our figures!
• The the random slopes are confounded with intercept, lets remove the correlation

L2test.3a<-lmer(Math ~ ActiveTime.GM*Told.C+Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.3a)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Told.C + Support.CC + (1 + Support.CC ||  
##     Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1067.1   1093.5   -525.5   1051.1      192 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9306 -0.5811 -0.0084  0.5860  3.3844 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 12.936   3.597   
##  Classroom.1 Support.CC  13.558   3.682   
##  Residual                 9.937   3.152   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)           73.5975     1.8121   3.9997  40.615 2.20e-06 ***
## ActiveTime.GM         11.5009     0.7625 193.6600  15.084  < 2e-16 ***
## Told.C                16.2252     3.6242   3.9997   4.477    0.011 *  
## Support.CC             3.0440     2.0045   3.8964   1.519    0.205    
## ActiveTime.GM:Told.C  10.4661     1.5261 193.2390   6.858 9.17e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Told.C Spp.CC
## ActiveTm.GM  0.000                     
## Told.C       0.000  0.004              
## Support.CC   0.000  0.019  0.000       
## ActT.GM:T.C  0.004 -0.031  0.000 -0.043

• Our main effect of Told came back and the model fitted better

anova(L2test.2,L2test.3a)

## Data: MLM.Data.2
## Models:
## L2test.2: Math ~ ActiveTime.GM * Told.C + (1 | Classroom)
## L2test.3a: Math ~ ActiveTime.GM * Told.C + Support.CC + (1 + Support.CC || Classroom)
##           npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## L2test.2     6 1091.4 1111.2 -539.70   1079.4                         
## L2test.3a    8 1067.1 1093.5 -525.55   1051.1 28.306  2  7.137e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Counfounded Random Slope

• What happens if we try to interact Support with Told
• The slope on support should basically decrease or disappear (cause we have so few classrooms and told conditions), why?
  • Because those random slopes of support are not really random! They can be explained by a fixed effect what the teacher was told
  • The same thing will happen if we do it with ActiveTime

L2test.4<-lmer(Math ~ ActiveTime.GM*Told.C+Support.CC*Told.C+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.4)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: 
## Math ~ ActiveTime.GM * Told.C + Support.CC * Told.C + (1 + Support.CC ||  
##     Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1060.9   1090.6   -521.5   1042.9      191 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0715 -0.5576  0.0091  0.6209  3.3709 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 12.937   3.597   
##  Classroom.1 Support.CC   0.000   0.000   
##  Residual                 9.904   3.147   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                      Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)           73.5981     1.8121   3.9997  40.614 2.20e-06 ***
## ActiveTime.GM         11.4833     0.7549 196.0197  15.211  < 2e-16 ***
## Told.C                16.2249     3.6243   3.9997   4.477 0.011020 *  
## Support.CC             3.0568     0.7846 195.9998   3.896 0.000134 ***
## ActiveTime.GM:Told.C  10.5940     1.5099 196.0197   7.016 3.62e-11 ***
## Told.C:Support.CC      7.2397     1.5692 195.9998   4.614 7.13e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Told.C Spp.CC AT.GM:
## ActiveTm.GM  0.000                            
## Told.C       0.000  0.004                     
## Support.CC   0.000  0.067  0.000              
## ActT.GM:T.C  0.004 -0.051  0.000 -0.095       
## Tld.C:Sp.CC  0.000 -0.095  0.000 -0.091  0.067
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• we can remove the random effect just test the for a three way (to speed things up)

L2test.4a<-lmer(Math ~ ActiveTime.GM*Told.C*Support.CC+(1|Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(L2test.4a)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Told.C * Support.CC + (1 | Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1042.4   1075.4   -511.2   1022.4      190 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.7532 -0.5890 -0.0383  0.5852  3.3567 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 12.20    3.493   
##  Residual               8.93    2.988   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                                 Estimate Std. Error       df t value Pr(>|t|)
## (Intercept)                      73.6591     1.7594   3.9983  41.867 1.95e-06
## ActiveTime.GM                    11.3861     0.7177 196.0116  15.865  < 2e-16
## Told.C                           16.0345     3.5187   3.9983   4.557   0.0104
## Support.CC                        3.2730     0.7506 196.0002   4.361 2.09e-05
## ActiveTime.GM:Told.C             10.3461     1.4354 196.0116   7.208 1.20e-11
## ActiveTime.GM:Support.CC         12.3497     2.6575 196.1172   4.647 6.17e-06
## Told.C:Support.CC                 7.9631     1.5012 196.0002   5.305 3.04e-07
## ActiveTime.GM:Told.C:Support.CC  -1.1512     5.3149 196.1172  -0.217   0.8288
##                                    
## (Intercept)                     ***
## ActiveTime.GM                   ***
## Told.C                          *  
## Support.CC                      ***
## ActiveTime.GM:Told.C            ***
## ActiveTime.GM:Support.CC        ***
## Told.C:Support.CC               ***
## ActiveTime.GM:Told.C:Support.CC    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Told.C Spp.CC AcT.GM:T.C AT.GM:S T.C:S.
## ActiveTm.GM  0.000                                               
## Told.C       0.000  0.004                                        
## Support.CC  -0.001  0.061  0.000                                 
## ActT.GM:T.C  0.004 -0.049  0.000 -0.100                          
## AcT.GM:S.CC  0.008 -0.028 -0.012  0.059 -0.036                   
## Tld.C:Sp.CC  0.000 -0.100 -0.001 -0.077  0.061      0.102        
## AT.GM:T.C:S -0.012 -0.036  0.008  0.102 -0.028     -0.076   0.059

• Check fit

anova(L2test.3a,L2test.4a)

## Data: MLM.Data.2
## Models:
## L2test.3a: Math ~ ActiveTime.GM * Told.C + Support.CC + (1 + Support.CC || Classroom)
## L2test.4a: Math ~ ActiveTime.GM * Told.C * Support.CC + (1 | Classroom)
##           npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
## L2test.3a    8 1067.1 1093.5 -525.55   1051.1                         
## L2test.4a   10 1042.4 1075.4 -511.21   1022.4 28.676  2  5.931e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Plot Final Model

# Set levels of support
SLevels.2<-c(mean(MLM.Data.2$Support.CC)-sd(MLM.Data.2$Support.CC),
                               mean(MLM.Data.2$Support.CC),
           mean(MLM.Data.2$Support.CC)+sd(MLM.Data.2$Support.CC))

Results.L2test.4a<-Effect(c("ActiveTime.GM","Support.CC","Told.C"),L2test.4a,
     xlevels=list(ActiveTime.GM=seq(-.5,.5,.2), 
                  Support.CC=SLevels.2,
                  Told.C=c(min(MLM.Data.2$Told.C),max(MLM.Data.2$Told.C)))) 

Results.L2test.4a<-as.data.frame(Results.L2test.4a)

Results.L2test.4a$Support.F<-factor(Results.L2test.4a$Support.CC,
                        levels=SLevels.2,
                         labels=c("Low Support", "Mean Support", "High Support"))


Results.L2test.4a$Told.F<-factor(Results.L2test.4a$Told.C,
                        levels=c(min(MLM.Data.2$Told.C),max(MLM.Data.2$Told.C)),
                         labels=c("Experimental","Works"))

Final.Fixed.Plot.3 <-ggplot(data = Results.L2test.4a, 
                            aes(x = ActiveTime.GM, y =fit, group=Support.F))+
  facet_grid(.~Told.F)+
  geom_line(size=2, aes(color=Support.F,linetype=Support.F))+
  coord_cartesian(xlim = c(-.5, .5),ylim = c(50, 100))+ 
  geom_ribbon(aes(ymin=fit-se, ymax=fit+se, group=Support.F, fill=Support.F),alpha=.2)+
  xlab("Proportion of Time Engaged in Active Learning \nCentered")+
  ylab("Math Score")+ 
  theme(legend.position = "top", 
        legend.title=element_blank())
Final.Fixed.Plot.3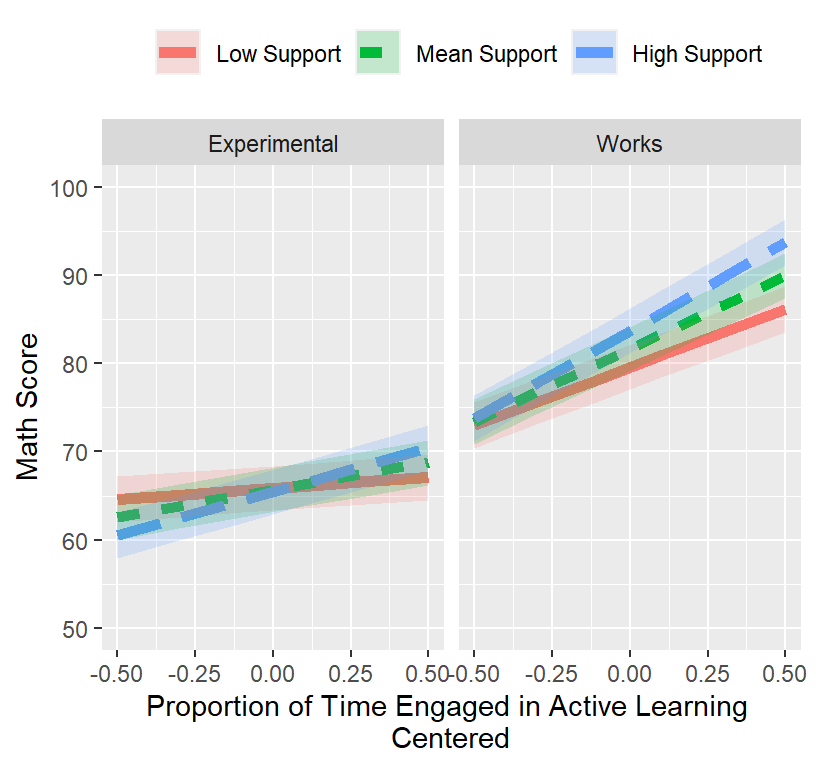

Recommenations

• Random slopes and intercepts can protect against deflation of SE and protect against type I error
• When to treat slopes and intercepts [plus their correlations] as random?
  • Ultra Conservative: Treat everything as random relative the cluster
    • Often results in failure for the model to fit (you will see lots of convergence errors)
  • Theory-Driven: Follow your design and theory as to what should be random
    • Sometimes theories are wrong and thus your model will not fit the data correctly
  • Data Driven: Use the best random structure for your data
    • Driving to the best fit does not always have meaning or make sense
  • Recommendation: Balance Theory and Data-driven approaches
    • Graph the data, see it follows your theories and if the random structure makes sense
    • Next, work towards a random structure that is logical and fits the data
• Balancing fixed and random effects
  • Sometimes your data cannot handle being treated as random and fixed
    • You cannot just treat everything as random as we saw because in this crazy case it was not really random (it was all sysmatic error due). This was an extreme example in some sense, but I have seen many times when the random structure falls apart. This is very common is small N or small clusters.
  • Other times you will add a random effect, and your effect of interest will disappear
    • Does that mean your results was type 1 error?
      • Not always: Watch your random structure closely, the correlations, and graph the model fit
      • Compare your fit to your spaghetti plots!
  • Watch carefully how the fixed effect and random effect change as you add new fixed term. As you add many fixed terms (you could have multicollinearity or suppression effects)