Degrees of Freedom and Pvalues

Problem with P-values

• What gives mixed-effects models their ability to handle complex designs (e.g., nested, crossed, nested & crossed, partially nested and crossed) is in part what does not allow them to calculate p-values
• Remember, \(t = \frac{M-\mu}{SE}\), where, \(SE = \sqrt\frac{\sigma^2}{n}\), \(df = n-1\)
• GLM uses standard error to determine significance: Required degrees of freedom to correct z-distribution for “sampling error” to produce \(t\) and \(F\) tables.
  
• But mixed models do not actually produce \(t\) or \(t^2=F\) values as they are not calculating the \(SE\) using the equation above, which uses observed - expected [mean square = \(\sigma^2 = \frac{SS}{N-1}\), where \(SS = (M-\mu)^2\)
• Instead, they estimate the \(SE\) using ML or REML function
• ML is a way of finding the value of one or more parameters in mixed model for a given statistic which makes the known likelihood distribution a maximum
  • likelihood is “a hypothetical probability that an event that has already occurred would yield a specific outcome” (http://mathworld.wolfram.com/Likelihood.html)
  • maximum is the largest value the function can produce
  • We will iterate through parameters until we maximize our likelihood
  • There are different ML (or just L) functions that can be used and they can apply to most distributions
• Problem 1: SE is not the one used in \(t\) and \(F\) (it does not use N)
• Problem 2: The estimate we get is not via OLS either, it’s via ML or REML (so what is the proper distribution to test against?)
• Problem 3: What is our \(DF\) even if we want to assume \(t\) and \(F\)?

Problem 3: DF Conceptual Issues

• Sample 500, 11the graders take the SAT from 3 schools partially nested in 2 economic districts

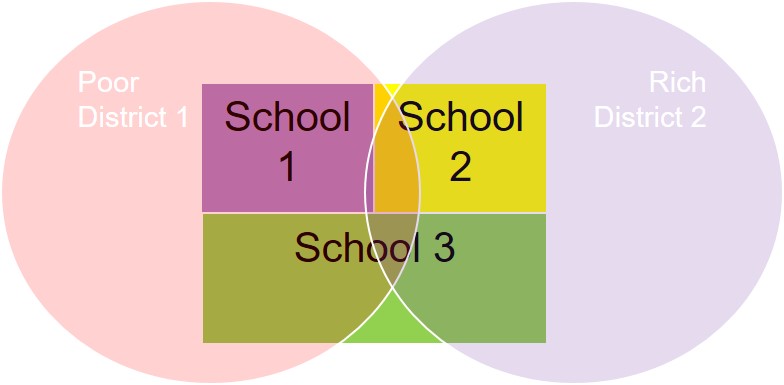
• Random sampling of 500 total from 3 schools [Note: school 3 is twice as large school 1 and 2]
• ANOVA Design: 1 factor: School OR district [they provide an unbalanced design so they can only be analyzed one at time]
• Assume homogeneity of variance of SAT score across schools and districts
• ANOVA can only ask 1 basic question: Are the means between the schools or districts different

ANOVA problem?

• Why is ANOVA bad here?
  • School 1 is predominately poor vs School 2 which is rich, so school 1 has less funding, larger classrooms sizes, more social issues at home and in school, fewer teachers, etc.
• This could impact both mean test scores and variance of test scores
  • Students from the poor district might have more diverse scores [high variance]
  • Student from rich district might have more similar scores, but higher average scores [low variance]
  • Poor students in the Rich school might also have changes in variance or mean test scores, which look very different from the poor or mixed school.

Mixed vs. ANOVA Solution

ANOVA Logic

• If we assume ANOVA that would mean we calculate mean/variance relative to their classification based on school and district [at the level we are examining only]
• In the case when all the variables are categorical, the DF “seems” logical, in that the proper MSerror terms could be calculated. However, in the mixed models, the random factors have been nested (kids in schools in districts).
  • So we cannot know how many of the people went into parsing the variance for each level of the random error term.
    • We could make assumptions, but some statisticians say over their dead bodies.
  • ANOVA is assumed to be robust against many violations, but that’s mostly only true in well-controlled balanced designs.
  • When ANOVA is stretched into the mixed model territory, it can result in unreasonable levels of type 1 error.

Mixed Logic

• 1. Fixed factors: School and District [student belongs to]
  • SAT score MEANS could be different depending on the school a kid goes to and what district they are from.
    
• 2. Random Factors: District, School, [Student]
  • SAT score VARIANCES could be different depending on the school a kid goes to and what district they are from.
    
  • So are the kids the DF, or the School or the district? What do with kids who are mismatched (poor but in richer schools or vice versa?)
• 3. Random Slopes: The impact of SES could be different depending on the school a kid goes to and what district they are from,
  • In the rich school, the SES of the student might not matter as much as the poor or mixed school
    • When we add random slopes, how many measurements of the effect of SES are we making - is it based on the number of students, schools or districts?
• Which level do we count the degrees of freedom for each fixed and random factor? Students, schools, or districts? How do we count DF for random factors?

Getting P-values

Path A: Don’t push your assumptions on me!

1. Modeling Fitting testing

• Likelihood ratio test [chi-square distribution]
• D = 2 - ln (Likelihood of null model / Likelihood of alternative model]
• Add/Remove fixed factors and test to see if model “fits the data better”
• Suggested by Bates and Bolker [least assumptions]
• FAST and well accepted [a bit anti-conservative some argue]
  • To do this you simply have to anova(model.1, model.2)

2. Bootstrapping

• Non-parametric: Re-sampling method where you resample with replacement from your own data
  • Common method in modern stats: A much better method then assuming normality and t-distributions
  • Example: You build your final model and you then take the subjects, resample them with replacement, and refit your model
    • You do this over and over again to build a distribution for each parameter in your model
      • You than calcuate the 95th percentile and see if contains zero, if not you have a significant effect
• Semi-parametric: Adds noise to the Non-parametric (assumes your measurements are randomly sampled from all possible measurements)
  • So you sample from your data, add parametric noise, rinse and repeat like above
• Parametric: You assume your data follows a specific distribution, you use your model to estimate the parameters, and then you simulate the study based on those parameters to estimate the CI. You than calcuate the 95th percentile and see if contains zero.
• So far we can only do Semi-parametric & Parametric because of the random effects
  • However, Semi-parametric is not fully implemented yet
• VERY, VERY SLOW.
• This procedure can fail because your model is unstable (probably means your model is bad anyway)
• You can also bootstrap Model fit testing (95th percentile method)

Path B: Let’s hold hands, put our fingers in our ears, and assume!

3. Assume z distributions to get p-values

• If you number of observations is high, just assume DF -> inf [so \(t > |2|\), is significant]
  • This is possible because you assume your random effects have controlled for the random variations in the populations and your values good estimates of the population
• Simulation studies by Barr et al. 2013 show this to be a reasonable assumption IF and ONLY OF random structure is MAXIMAL
  • This is debated by Bates et al, 2015 and we will come back to this in a few weeks

4. Estimate degrees of freedom

• SAS/SPSS uses Satterthwaite approximations
  • However, there are also Kenward-Roger approximations [see Westfall, Kenny, & Judd, 2014]
  • Either is acceptable, but KR is recommended (but does not always work)
• Makes a number of assumptions, will mirror results of traditional ANOVA fairly closely [as you would expect when you make similar assumptions about DF]
  • This method can also fail to work because your model is unstable/convergence problems

Path C: Go Bayesian

• There use to be a way to get pvalues based on Markov-chain Monte-carlo methods (MCMC), but has been hard to implement in complex designs
  • Currently does not work for lme4 package we are using
• You have to refit the model as Bayesian using rstanarm and get CIs
  • We will not do this (see Gelman & Hill textbook on Multilevel models for Bayesian approach)

Practical solution

• Practically, when you add factors in stepwise and model fit shows a significant improvement (Path 1A) you will see the new factors has a t > 2. (Path 2A)
• That does not always agree with bootstrapping (Path 1B) or ANOVA-like degrees of freedom (Path 2B)
  • This is because LME4 package we are using does not allow us to control for the heterogeneous variance problem. The older package LME will allow you control for it.
    • Note LME uses Satterthwaite approximations and will always give you DF and pvalues
  • Also, there could be other problems with your assumptions that bootstrapping is picking up on the other paths will not pick up
• Recommendation: Based on current trends:
  1. Always do Path 1A to say the model is better
  2. To test the parameters add Path 1B, Path 2A or 2B.
     • I usually pick 1B or 2A
     • But some fields might demand DF, so you have to do 2B

Multi-Level Model Design Example

• Same as Last Week Simulation (version 2)
• Let’s examine our paths!

Design Reminder

• You want to measure how students respond to a new type of active learning method (computer-based) in math class
• You measure students math scores (DV) and the proportion of time (IV) they spend using the computer (which you assign)
• You also measure how supportive (control and/or moderator) each student feels the teacher is about this new method.
  • Also, maybe if the students feel the teacher approves of the new method, they might engage with it more
• You tell two the teachers that the active learning method works and the other two its experimental [Told level 2 variable]
• You have access to different classrooms with 50 students per class

Simulation Details

• Set the different slope of proportion of time (plus noise)
• Different intercept per class (plus noise) [which will implicitly correlate with supportive]
• Different slope per class on supportive (plus noise)
• Set same interaction between proportion of time and supportive
• Teachers in Classrooms 1 and 2 were Told the program works and 3 & 4 that it is experimental
• [Note: I have not shown the simulation ‘echo=FALSE’ does not print it]

Plot our Clusters

• Students nested in classrooms

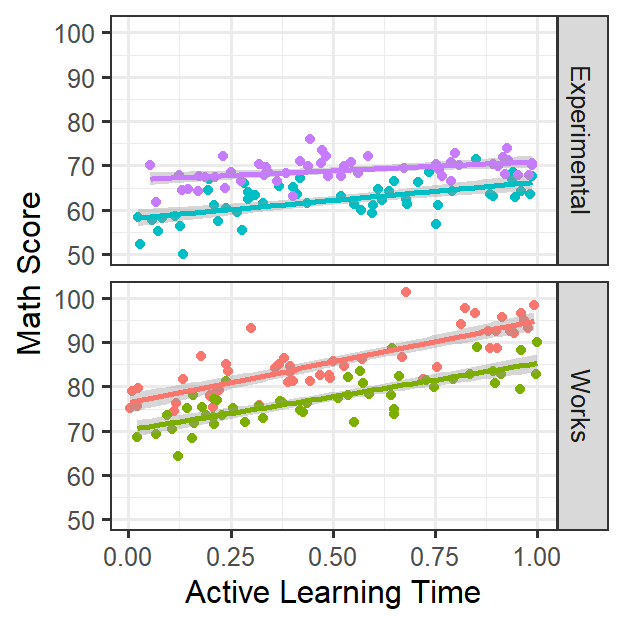
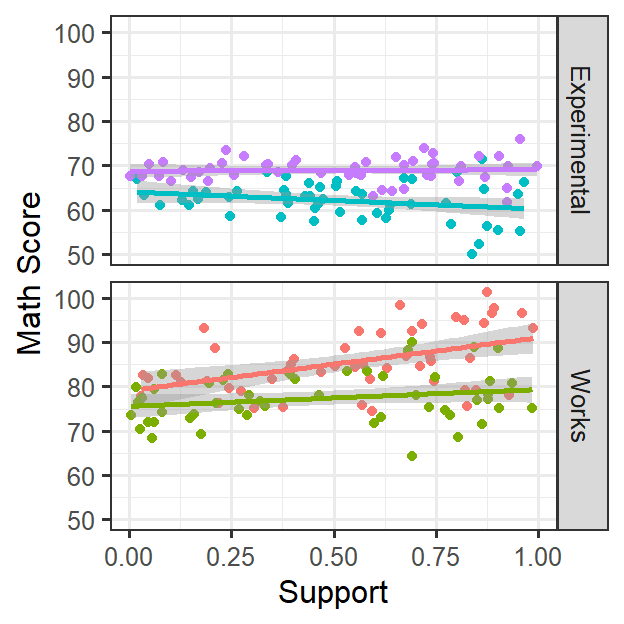
• Let’s center the data just as before, but layer fixed effects (keep random effects constant)

Path 1A & 2A

Null Model

library(plyr)
library(lme4)
MLM.Data.2$ActiveTime.GM<-scale(MLM.Data.2$ActiveTime,scale=F)
MLM.Data.2<-ddply(MLM.Data.2,.(Classroom), mutate, ClassSupport = mean(Support))
MLM.Data.2$Support.CC<-MLM.Data.2$Support-MLM.Data.2$ClassSupport

MLM.Model.1<-lmer(Math ~ 1+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)

Main effects

MLM.Model.2<-lmer(Math ~ ActiveTime.GM+Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)

Interaction

MLM.Model.3<-lmer(Math ~ ActiveTime.GM*Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)

Devience testing [Assume Chi-Square distrobution]

anova(MLM.Model.1,MLM.Model.2,MLM.Model.3)

## Data: MLM.Data.2
## Models:
## MLM.Model.1: Math ~ 1 + (1 + Support.CC || Classroom)
## MLM.Model.2: Math ~ ActiveTime.GM + Support.CC + (1 + Support.CC || Classroom)
## MLM.Model.3: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
##             npar    AIC    BIC  logLik deviance   Chisq Df Pr(>Chisq)    
## MLM.Model.1    4 1241.5 1254.6 -616.72   1233.5                          
## MLM.Model.2    6 1112.3 1132.0 -550.13   1100.3 133.192  2  < 2.2e-16 ***
## MLM.Model.3    7 1096.8 1119.9 -541.42   1082.8  17.422  1  2.994e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Deviance testing [Bootstrapped]

• You only do this two at a time
• You have to follow this syntax PBmodcomp(largeModel, smallModel, nsims)
  • LRT: Assuming that LRT has a chi-square distribution (what we did above)
  • PBtest: The fraction of simulated LRT-values that are larger or equal to the observed LRT value.
    • Conservative relative to LRT
• SLLOOOWWWWWWW [you might want to reduce the sims when you run this on your laptops]
  • Yes the number of simulations make a difference (go for 1-2K when you publish just to be sure)

library(pbkrtest)
PBmodcomp(MLM.Model.2,MLM.Model.1,nsim=500)

## Bootstrap test; time: 10.08 sec; samples: 500; extremes: 0;
## large : Math ~ ActiveTime.GM + Support.CC + ((1 | Classroom) + (0 + Support.CC | 
##     Classroom))
## Math ~ 1 + ((1 | Classroom) + (0 + Support.CC | Classroom))
##          stat df   p.value    
## LRT    133.19  2 < 2.2e-16 ***
## PBtest 133.19     0.001996 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

PBmodcomp(MLM.Model.3,MLM.Model.2,nsim=500)

## Bootstrap test; time: 9.83 sec; samples: 500; extremes: 0;
## large : Math ~ ActiveTime.GM * Support.CC + ((1 | Classroom) + (0 + Support.CC | 
##     Classroom))
## Math ~ ActiveTime.GM + Support.CC + ((1 | Classroom) + (0 + Support.CC | 
##     Classroom))
##          stat df   p.value    
## LRT    17.422  1 2.994e-05 ***
## PBtest 17.422     0.001996 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Bootstrap Final Model

Parametric Version

• Take bootstrap distribution and find percentiles (usually, .025 and .975)

Model.Final.CI.boot <- confint(MLM.Model.3, method="boot",nsim=500,boot.type = c("perc")) 
Model.Final.CI.boot

##                               2.5 %    97.5 %
## .sig01                    1.9481106 13.404665
## .sig02                    0.0000000  6.524522
## .sigma                    2.9991435  3.654218
## (Intercept)              64.7011766 82.241833
## ActiveTime.GM            10.0468297 13.219119
## Support.CC               -0.2783821  8.181753
## ActiveTime.GM:Support.CC  6.7860989 19.128069

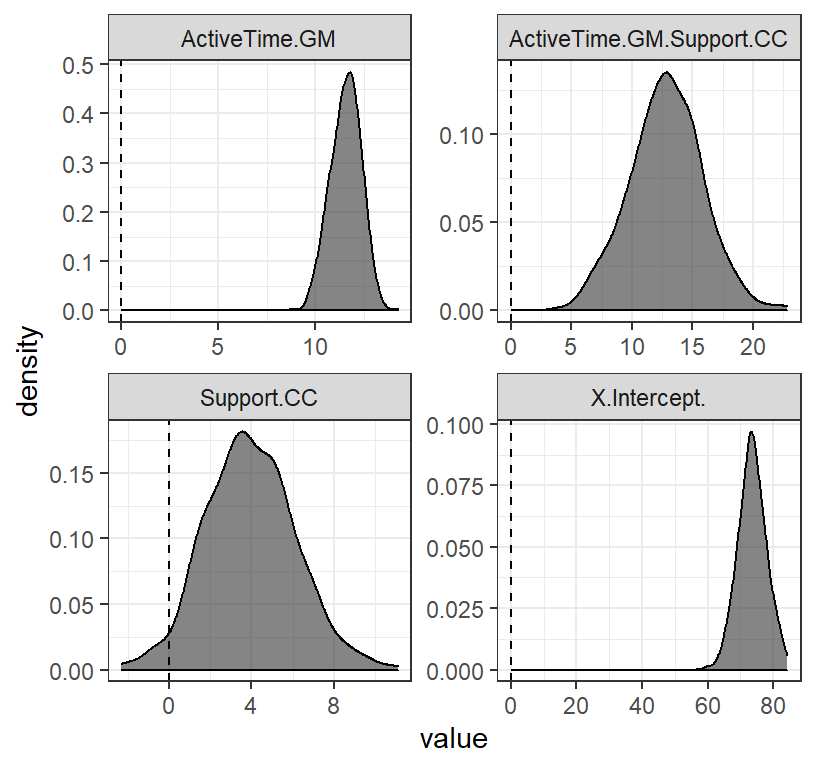
• Lets visualize the bootstrapping on the fixed effects

bfixed <- bootMer(MLM.Model.3, FUN=fixef,nsim=500)

library(ggplot2)
library(tidyr)
bfixed$t %>%
  data.frame()%>%
  gather()%>%
  ggplot(aes(value))+
  stat_density(alpha = 0.6, color = "black")+
  geom_vline(xintercept = 0, linetype = 2)+
  facet_wrap(~key, scales = "free")+
  theme_bw()

Path 2B

Satterthwaite Degrees of freedom

• We need to refit out model using a new package

library(lmerTest)
MLM.Model.3.LTest<-lmerTest::lmer(Math ~ ActiveTime.GM*Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(MLM.Model.3.LTest)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1096.8   1119.9   -541.4   1082.8      193 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.80667 -0.61518  0.09629  0.58731  3.15071 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 76.44    8.743   
##  Classroom.1 Support.CC  14.87    3.857   
##  Residual                11.28    3.358   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                          Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)                73.611      4.378   4.000  16.814 7.34e-05 ***
## ActiveTime.GM              11.579      0.812 193.715  14.260  < 2e-16 ***
## Support.CC                  3.836      2.104   3.838   1.823    0.145    
## ActiveTime.GM:Support.CC   12.770      2.982 192.911   4.283 2.90e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Spp.CC
## ActiveTm.GM  0.000              
## Support.CC   0.000  0.018       
## AcT.GM:S.CC  0.003 -0.022  0.022

• Because Support.CC is random slope, we only have 4 schools, thus DF changes to match how many slopes we measured
• If we want the model in ANOVA style format we can get that as well

library(lmerTest)
anova(MLM.Model.3.LTest)

## Type III Analysis of Variance Table with Satterthwaite's method
##                           Sum Sq Mean Sq NumDF   DenDF  F value    Pr(>F)    
## ActiveTime.GM            2293.12 2293.12     1 193.715 203.3439 < 2.2e-16 ***
## Support.CC                 37.49   37.49     1   3.838   3.3246    0.1453    
## ActiveTime.GM:Support.CC  206.89  206.89     1 192.911  18.3463 2.903e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Notice DF changes

• No random slopes

MLM.Model.4.LTest<-lmerTest::lmer(Math ~ ActiveTime.GM*Support.CC+(1|Classroom),  
              data=MLM.Data.2, REML=FALSE)
summary(MLM.Model.4.LTest)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Support.CC + (1 | Classroom)
##    Data: MLM.Data.2
## 
##      AIC      BIC   logLik deviance df.resid 
##   1105.8   1125.6   -546.9   1093.8      194 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.0219 -0.5960  0.0471  0.5869  3.3549 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  Classroom (Intercept) 76.64    8.755   
##  Residual              12.38    3.519   
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                          Estimate Std. Error       df t value Pr(>|t|)    
## (Intercept)               73.6058     4.3844   3.9996  16.788 7.38e-05 ***
## ActiveTime.GM             11.9604     0.8398 196.0048  14.243  < 2e-16 ***
## Support.CC                 4.0951     0.8725 195.9998   4.693 5.04e-06 ***
## ActiveTime.GM:Support.CC  11.5995     3.0999 196.0423   3.742  0.00024 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Spp.CC
## ActiveTm.GM  0.000              
## Support.CC   0.000  0.053       
## AcT.GM:S.CC  0.003 -0.022  0.073

• You will notice the degrees of freedom change

Kenward-Roger Degrees of freedom

• These might be SLOW and might fail in large data sets
• Must be fit with REML

library(pbkrtest)

MLM.Model.3.LTest.REML<-lmerTest::lmer(Math ~ ActiveTime.GM*Support.CC+(1+Support.CC||Classroom),  
              data=MLM.Data.2, REML=TRUE)
summary(MLM.Model.3.LTest.REML, ddf="Kenward-Roger")

## Linear mixed model fit by REML. t-tests use Kenward-Roger's method [
## lmerModLmerTest]
## Formula: Math ~ ActiveTime.GM * Support.CC + (1 + Support.CC || Classroom)
##    Data: MLM.Data.2
## 
## REML criterion at convergence: 1069
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.80023 -0.60826  0.09906  0.58608  3.11201 
## 
## Random effects:
##  Groups      Name        Variance Std.Dev.
##  Classroom   (Intercept) 101.99   10.099  
##  Classroom.1 Support.CC   21.03    4.586  
##  Residual                 11.39    3.375  
## Number of obs: 200, groups:  Classroom, 4
## 
## Fixed effects:
##                          Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)                73.612      5.055   3.000  14.562 0.000702 ***
## ActiveTime.GM              11.558      0.819 191.349  14.113  < 2e-16 ***
## Support.CC                  3.823      2.445   2.990   1.564 0.216108    
## ActiveTime.GM:Support.CC   12.817      3.002 190.767   4.269 3.09e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) AcT.GM Spp.CC
## ActiveTm.GM  0.000              
## Support.CC   0.000  0.015       
## AcT.GM:S.CC  0.003 -0.022  0.019

Practical Issues

• The effects package will generate CIs for mixed models, but will approximate them as below:

Model.Final.CI.Wald <- confint(MLM.Model.3, method="Wald") 

• You can force the effects package to do them as KR, buts its slow (and you’re probably cannot see the difference anyway)
• Visualizing the bootstrapped ones is difficult and takes a fair bit of code work
  • I will try to find a function that does this, but so far no luck
• I usually just graph the effects version and either show SE or CI
  • There is not a perfect solution, but the point is just to give your reader some idea of the error
  • These may not always match your “significance” and this will be a bigger problem later when we have repeated designs