Subjects & Items: Maximal

1 Random Items (Stimulus)

Imagine you are running a study on attentional blink and you want to see if disturbing images cause a longer attentional blink depending on whether you warn the subjects of what they are about to see (A: Few Details, B: Many Details). You select a bunch of disturbing images, but the problem is that not all image types have the same effect. The multiple images within each condition, for whatever reason, yield a noisy response. For example, images of people eating bugs vs. people swimming in sewage maybe have the same mean rating of grossness in your norming study (asking lots of people to rate the items), but there is variance around those items. What happens if different levels of warnings influence the specific types of items? If we counterbalance our design, we can measure the effect of the condition on the items and subjects. The goal is to know that our condition is causing an effect on our subjects (not our items). We want to make sure our experiment generalizes over both subjects and items!

Barr et al., 2013 summarizes the ANOVA approach to detailing with subject and items. Items are not independent measures of the effect (like with subjects). Thus we violate independence (inflate Type 1 error). The solution was to run \(F_1\) ANOVA, where the random term was the subject and \(F_2\) where the random term was the items. You want a significant effect of your condition on both \(F_1\) and \(F_2\) ANOVA (Note, however: the more the effect varies across items/subjects the higher the risk of type I error). The solution to reducing Barr et al., 2013 proposed to reduce the type I error rate and increase the power (and run one analysis) is to use the maximal random structure.

2 Subjects and Items Maximal Structure

Counterbalanced Designs - All subjects saw all experimental conditions (A & B), and Items (1:6) but balanced across condition. Subjects saw condition A and B 3 times each.

Subject	Items 1	Items 2	Items 3	Items 4	Items 5	Items 6
1	A	B	A	B	A	B
2	B	A	B	A	B	A
3	A	B	A	B	A	B
4	B	A	B	A	B	A
5	A	B	A	B	A	B
6	B	A	B	A	B	A

• With this many repeats of the conditions, we can estimate the random effects around the items
• For this type of design the maximal structure is (1+Condition|Subject) + (1+Condition|Item)
  • Crossed random effects
  • We will estimate the random slopes of condition per subject and per item

2.1 Applicable Designs

Random slopes per item only makes sense in specific designs (see Westfall et al., 2014)

Fully crossed: (1+Condition|Subject) + (1+Condition|Item) + (1|Subject:Item)

Subject	Stimuli 1	Stimuli 2
1	AB	AB
2	AB	AB

Counterbalanced: (1+Condition|Subject) + (1+Condition|Item)

Subject	Stimuli 1	Stimuli 2
1	A	B
2	B	A

Subjects-within Condition: (1|Subject) + (1+Condition|Item) (subjects are nested in condition)

Subject	Stimuli 1	Stimuli 2
1	A	A
2	B	B

But not in these designs (as conditions are nested in items)

Items-within condition: (1+Condition|Subject) + (1|Item) (subjects are crossed with condition, but not items)

Subject	Stimuli 1	Stimuli 2
1	A	B
2	A	B

Items and subjects within condition: (1|Subject) + (1|Item)

Subject	Stimuli 1	Stimuli 2
1	A
2		B

2.2 Simulation

• Simulate (using RePsychLing package functions Bates et al., 2015) where we set the \(H_0\) to be FALSE
• We will examine the results By Subject and By Item for a Counterbalanced Design with 6 subjects and 6 items.
• Simulation results in Download Data
• Check our design

DataSim6<-read.csv("Mixed/DataSim6.csv")
mytable <- table(DataSim6$subj,DataSim6$item,DataSim6$cond) # A will be rows, B will be

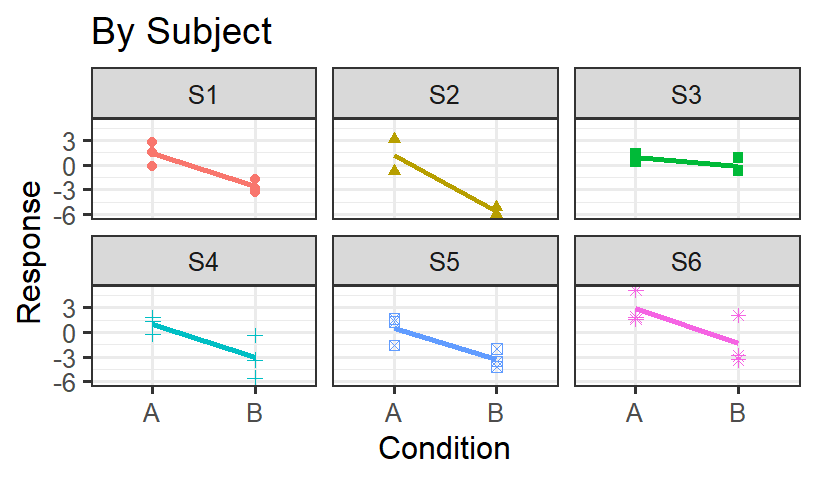
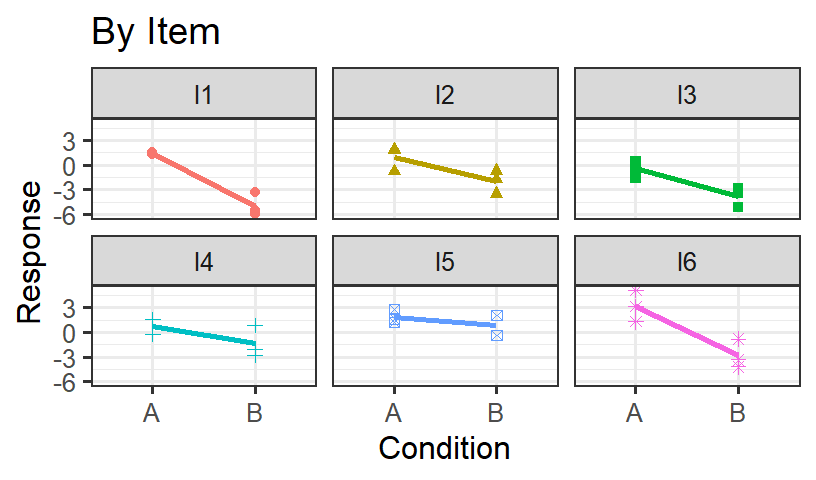
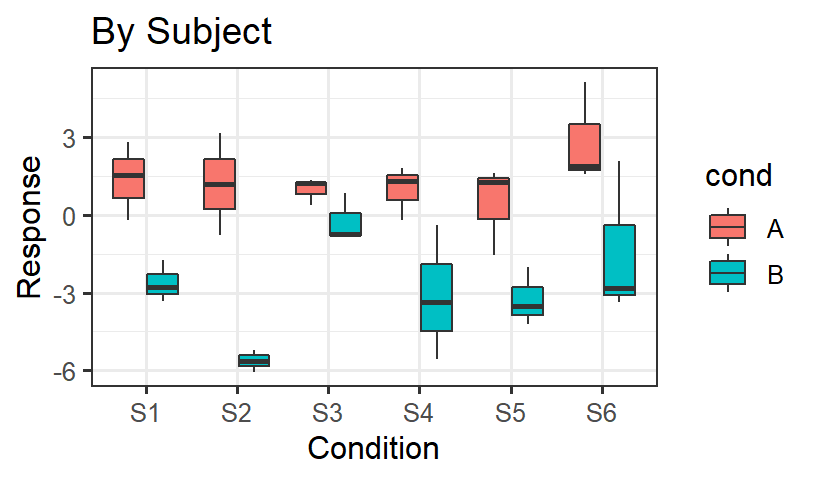
• It easier to see the variance per subject and per item sometimes as boxplots

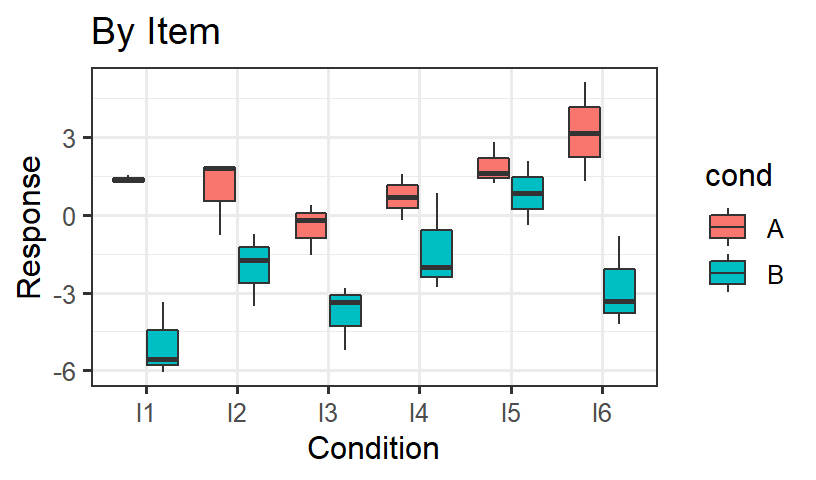
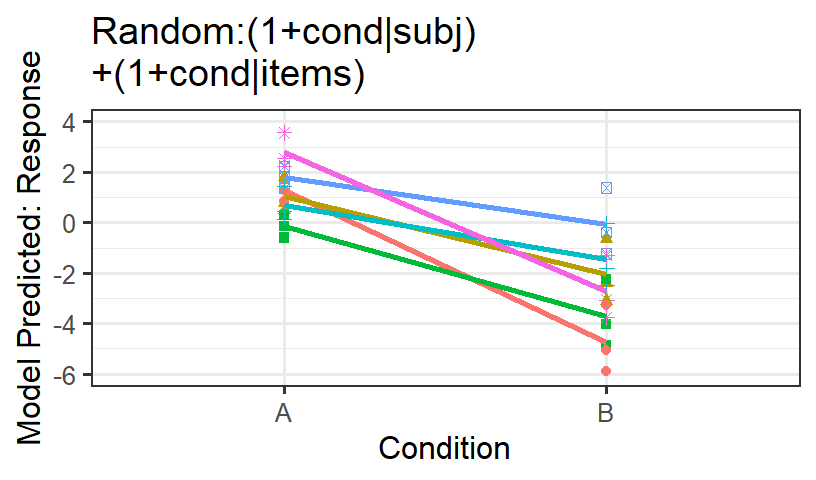
2.2.1 Random Subjects

• Fit only random intercepts of Subjects and random slopes of condition (1+cond|subj)
• We will examine the ICC to see what subjects (level 2) capture
• We will also predict model results and visually examine our fit

library(lme4)

Sub.Only.Fit<-lmer(resp~cond+(1+cond|subj),data=DataSim6,REML=FALSE)
sjstats::icc(Sub.Only.Fit)
DataSim6$S.Fitted<-predict(Sub.Only.Fit, newdata=DataSim6)

## [1] NA

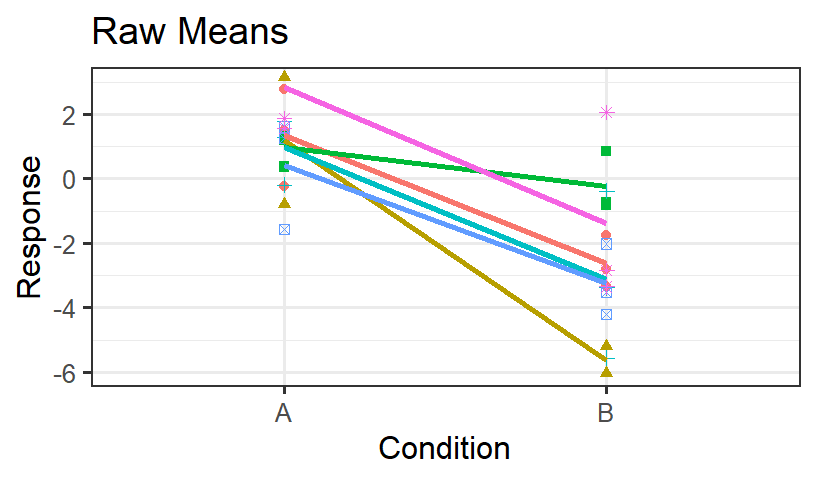
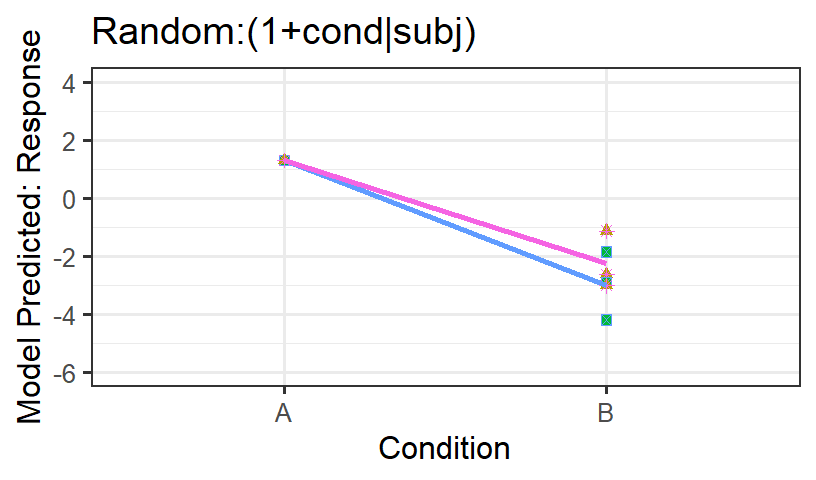
• Subjects alone is not doing a good job
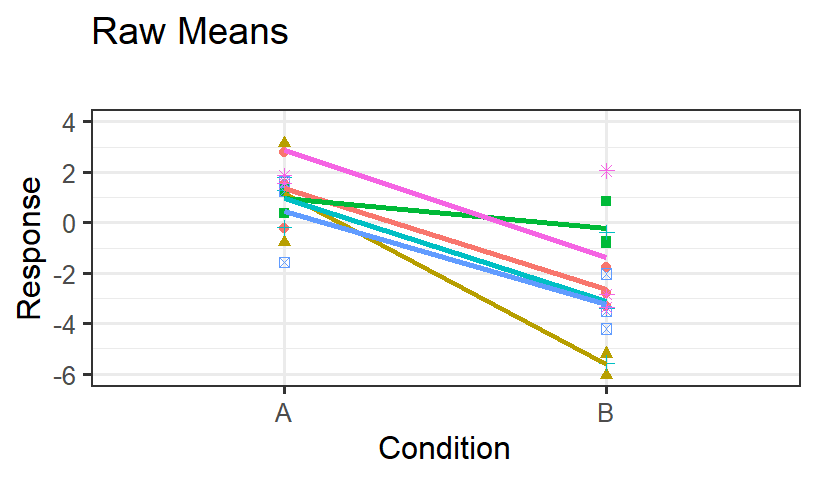
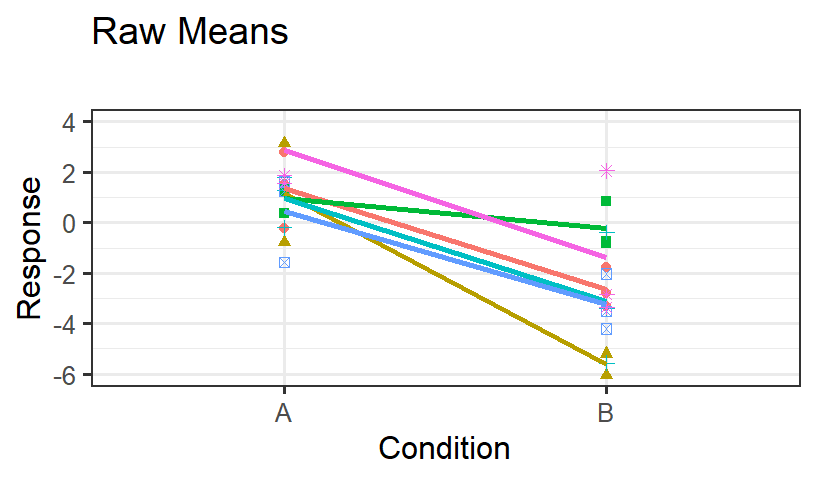
• Let’s see what the model predicts for subjects

• Let’s see what the model predicts for items

• Examine the model results

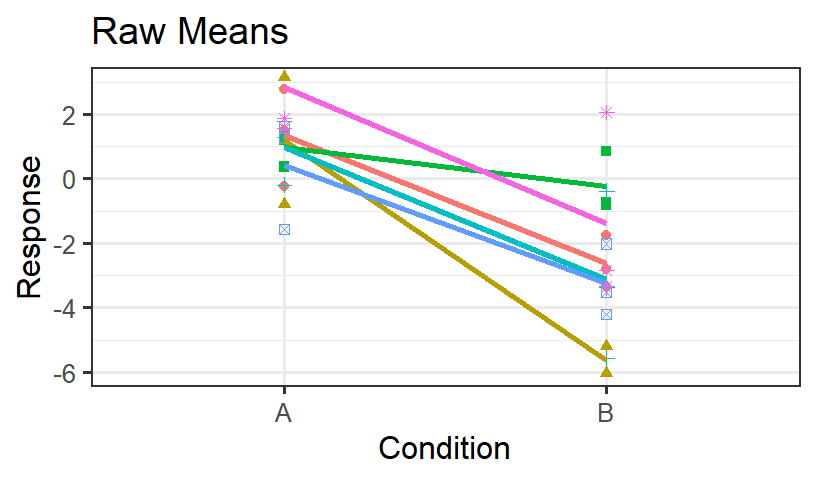
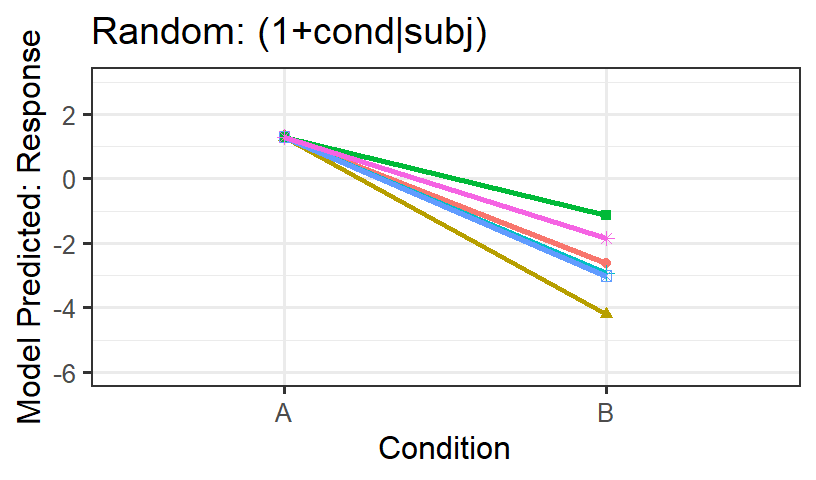
summary(Sub.Only.Fit)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: resp ~ cond + (1 + cond | subj)
##    Data: DataSim6
## 
##      AIC      BIC   logLik deviance df.resid 
##    148.6    157.7    -68.3    136.6       28 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.72830 -0.60114 -0.01594  0.33334  2.35492 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  subj     (Intercept) 0.000    0.000        
##           condB       1.529    1.237     NaN
##  Residual             2.755    1.660        
## Number of obs: 34, groups:  subj, 6
## 
## Fixed effects:
##             Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)   1.3007     0.4025 27.1785   3.231  0.00322 ** 
## condB        -3.9262     0.7622  9.1582  -5.151  0.00057 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##       (Intr)
## condB -0.528
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• We can see significant result on the fixed effect, but problems with the random correlations (which we will ignore for now)

2.2.2 Random Subjects & Items

• Fit only random intercepts of Subjects & Items and random slopes of condition (1+cond|subj)+(1+cond|item)
• We will examine the ICC to see what subjects & Items (level 2) captures
• We will also predict model results and visually examine our fit

Sub.Items.Fit<-lmer(resp~cond+(1+cond|subj)+(1+cond|item),data=DataSim6,REML=FALSE)
sjstats::icc(Sub.Items.Fit)
DataSim6$SI.Fitted<-predict(Sub.Items.Fit, newdata=DataSim6)

## # Intraclass Correlation Coefficient
## 
##     Adjusted ICC: 0.782
##   Unadjusted ICC: 0.404

• Subjects & Items are picking variance now
• Let’s see what the model predicts for subjects

• Let’s see what the model predicts for items

• Examine the model results

summary(Sub.Items.Fit)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: resp ~ cond + (1 + cond | subj) + (1 + cond | item)
##    Data: DataSim6
## 
##      AIC      BIC   logLik deviance df.resid 
##    141.3    155.0    -61.6    123.3       25 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -1.40501 -0.48644 -0.02899  0.53637  1.71396 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr 
##  subj     (Intercept) 0.3646   0.6039        
##           condB       0.6507   0.8067   0.60 
##  item     (Intercept) 1.1097   1.0534        
##           condB       3.2387   1.7996   -0.41
##  Residual             0.8199   0.9055        
## Number of obs: 34, groups:  subj, 6; item, 6
## 
## Fixed effects:
##             Estimate Std. Error      df t value Pr(>|t|)   
## (Intercept)   1.2363     0.5433  6.6570   2.275  0.05892 . 
## condB        -3.6968     0.8645  6.7724  -4.276  0.00396 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##       (Intr)
## condB -0.275

• We see a drop in the t-value from the subjects only model

2.3 Maximal Random Structure vs Simpler Random effects (Counterbalanced Designs)

• Question is all this complexity needed? Can’t we do an intercepts only model, ignore items, or simply go back to our ANOVA?

2.3.1 Type I Error

• Barr et al, 2013 have found that type I error is extremely high when we ignore maximal structure
• To show this, I simulated a larger design (24 subjects and 24 items in a 2 level counterbalanced design) 1K times with \(H_0\) = TRUE. This means we can estimate the type I error rate of different types of fit. [Using RePsychLing Functions]
  • 5% of the data was allowed to be missing at random
    
• See the results below read in from the Type1.csv file
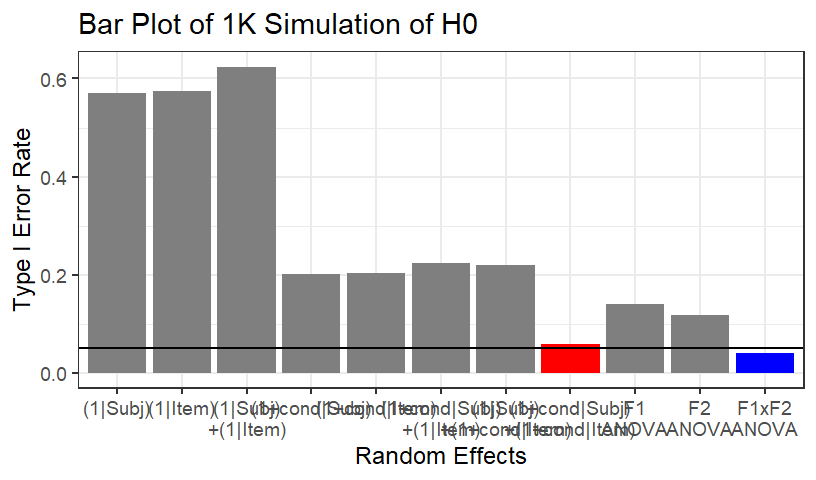
  • When you set an intercept-only model (subject and/or items) your Type I error rate was nearly 60%
  • When you set a random slope & intercept model but only for subject or items your Type I error rate was nearly 20%
  • F1xF2 ANOVA was about 4.1% (with F1 or F2 alone being 11-14%)
  • The maximal model (1+cond|Subj+(1+cond|Item) yielded an acceptable Type 1 error rate of 5.9%, simply using the anticonservative method of |t| > 2 as the threshold for significance (more conservative methods for Pvalues will probably bring it below 5%)

2.3.2 Power Level

• How does this complexity impact our power?
• Barr et al, 2013 have found that power is reduced by having this complex structure, but in general is better than F1xF2 ANOVA
• Same simulation as above, but this time \(H_0\) = FALSE. So we can calculate the number of times we get a significant effect
  • 5% of the data could be missing at random
    
• See the results below read in from the Power.csv file
  • When you set an intercepts only model (subject and/or items) your power was nearly 96%
  • When you set random slopes & intercept model but only for subject or items your power was nearly 80%
  • F1xF2 ANOVA was about 41% (with F1 or F2 alone being 55-60%)
  • The maximal model (1+cond|Subj+(1+cond|Item) yielded a power of 63%, using |t| > 2 as the threshold for significance

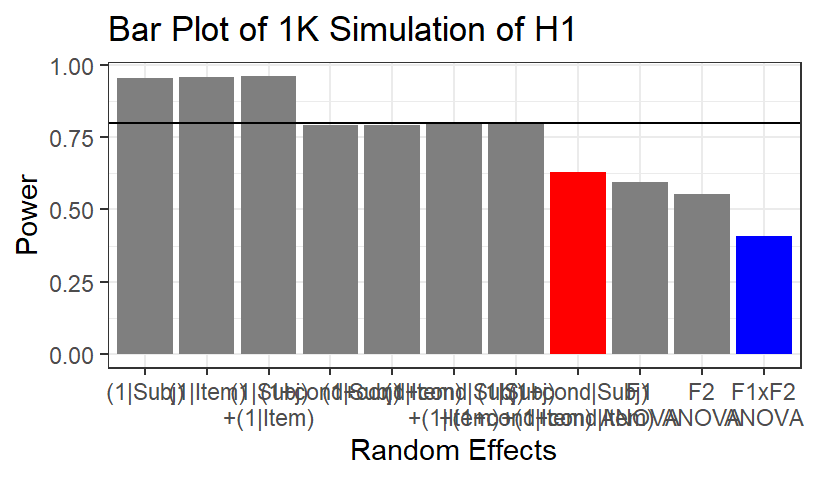
• All things being equal the Mixed Model > F1xF2 ANOVA (less Type 1 & Higher Power)
• The mixed model will allow for more complex designs than ANOVA
  • For additional simulation see http://talklab.psy.gla.ac.uk/simgen/.
  • They provide extensive simulation work

2.4 Convergence & Optimation

• Maximal modeling is the most complex random structure that you can apply to the data and it assumes that there is sufficient variance at the subjects and items (and for random slopes at both subjects and items) to sustain this model
  • In this case, your model will fail to converge: meaning it cannot estimate random effects (you will see lots of warning messages)
    • Usually, the problem is the random structure is too complex for the data
  • Sometimes this is optimization issue (the functions used to estimate model parameters) and not a problem with the random structure: https://github.com/lme4/lme4/issues/98
    • The functions can be changed and the models can be refit (but in my experience this often fails)
    • Optimization Options: There are options, but details are beyond are scope today, but here is an example of how to change them:

#https://github.com/lme4/lme4/issues/98
library(nloptr)
defaultControl <- list(algorithm="NLOPT_LN_BOBYQA",xtol_rel=1e-6,maxeval=1e5)
nloptwrap2 <- function(fn,par,lower,upper,control=list(),...) {
    for (n in names(defaultControl)) 
      if (is.null(control[[n]])) control[[n]] <- defaultControl[[n]]
    res <- nloptr(x0=par,eval_f=fn,lb=lower,ub=upper,opts=control,...)
    with(res,list(par=solution,
                  fval=objective,
                  feval=iterations,
                  conv=if (status>0) 0 else status,
                  message=message))
}
Sub.Items.Fit.N <- update(Sub.Items.Fit,control=lmerControl(optimizer="nloptwrap2"))
deviance(Sub.Items.Fit)-deviance(Sub.Items.Fit.N)

## [1] 6.150186e-08

• another option:

library("optimx")
Sub.Items.Fit.O <-lmer(resp~cond+(1+cond|subj)+(1+cond|item),data=DataSim6,REML=FALSE,
     control = lmerControl(optimizer = "optimx", 
                           optCtrl = list(method = "nlminb",
                                          starttests = FALSE, kkt = FALSE)))
deviance(Sub.Items.Fit)-deviance(Sub.Items.Fit.O)

## [1] 6.150155e-08

• In both cases, the fit has not improved

2.4.1 Convergence Suggestions

• Barr et al., suggest you stepwise down the complexity of the random effects until the model converges, for example:

1. Maximal: (1+cond|Subj)+(1+cond|Item)
2. (1+cond||Subj)+(1+cond||Item): remove random correlations (try one at time) 3.(1+cond|Subj+(1|Item): remove random slopes (try one at time) and/or also random correlations 4.(1|Subj+(1|Item): remove all slopes (but Type I error galore!?)

• We will return next week to Bates et al. criticisms of the Maximal approach and their solutions to keeping the random structure as complex as it needs to be

2.5 Maximal Structure for Multiple Repeated Factors

• If you had multiple repeated factors, they need to be treated as random slopes as well:
  • (1+cond1*cond2|Subj)+(1+cond1*cond2|Item)
    • This means we will estimate 3 random slopes per subject and 3 more per item (and random correlations between them)
• Everyone I have talked too finds this rarely converges
  • Also, this can be very slow (as you add more and more random effects the slower it will get)

2.5.1 Convergence Suggestions

1. Maximal: (1+cond1*cond2|Subj)+(1+cond1*cond2|Item)
2. (1+cond1+cond2|Subj)+(1+cond1+cond2|Item): remove interactions
3. (1+cond1+cond2||Subj)+(1+cond1+cond2||Item): remove random correlations (one at a time)
4. (1+cond1+cond2||Subj)+(1+cond1||Item): remove random slopes (try one at time) and/or also random correlations
5. This is often trial and error as to which combination will work

• Again, Bates solution address some of these issues

2.6 Maximal Structure & Non-Gaussian Distributions

If you use Logistic or Poisson you will encounter serious convergence issues, if a) you sample size is small or b) the number of items you have is small. Rarely do I find that maximal model fits. However, I also find the I must try many different optimizers.

3 Coding Types

Problem with categorical data is that how you code it affects your random effect estimation. The best suggestion is when you work with 2 level factors, convert them to -.5 and .5 and treat them like slopes! They are easiest to work with. Dummy coding can work equally as well, but you have to code it more carefully. We will go over that in the in-class assignment. See here for more details click here