Multiple Regression

Causal Modeling

• X causes Y. Eating too many cookies will make you gain weight
• We need to make sure that the cause is not spurious.
  • Causal Path analysis
    • Direct and Indirect Effects
      • Direct: X1 -> Y (which can control for X2)
      • Indirect X1 -> X2 -> Y

Partial Redundancy (most common issue)

• There are a few possibilities

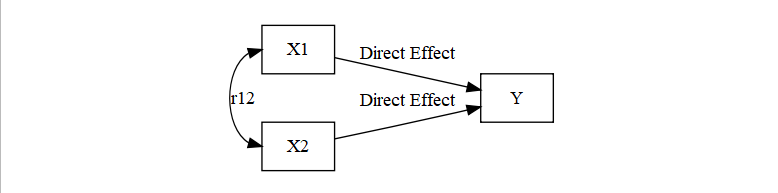
• Both X1 and X2 are causing Y

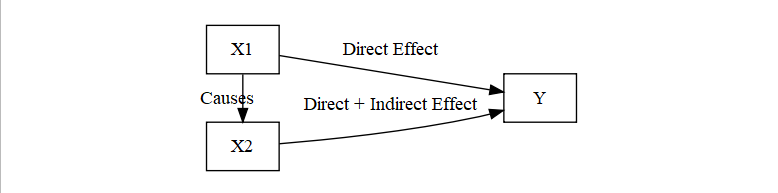
• X1 and X2 are causing Y, but X1 is causing X2 thus making X2 indirect as well

• Both occur when: \(r_{Y1} > r_{Y2}r_{12}\) & \(r_{Y2} > r_{Y1}r_{12}\)

• Hard to know whether you have the Model A or B

Back to our last weeks example

• Practice Time (X1)
• Performance Anxiety (X2)
• Memory Errors (Y)

Variable	Practice Time (X1)	Performance Anxiety (X2)	Memory Errors (Y)
Practice Time (X1)	1	.3	.6
Performance Anxiety (X2)	.3	1	.4
Memory Errors (Y)	.6	.4	1

• Model we used was Memory (Y) ~ Slope Practice(X1) + Slope Anxiety (X2) + Intercept

library(MASS) #create data
py1 =.6 #Cor between X1 (Practice Time) and Memory Errors
py2 =.4 #Cor between X2 (Performance Anxiety) and Memory Errors
p12= .3 #Cor between X1 (Practice Time) and X2 (Performance Anxiety)
Means.X1X2Y<- c(10,10,10) #set the means of X and Y variables
CovMatrix.X1X2Y <- matrix(c(1,p12,py1,
                            p12,1,py2,
                            py1,py2,1),3,3) # creates the covariate matrix 
set.seed(42)
CorrDataT<-mvrnorm(n=100, mu=Means.X1X2Y,Sigma=CovMatrix.X1X2Y, empirical=TRUE)
#Convert them to a "Data.Frame" & add our labels to the vectors we created
CorrDataT<-as.data.frame(CorrDataT)
colnames(CorrDataT) <- c("Practice","Anxiety","Memory")

• Use the stargazer package to see the models side by side
• Change latex below to text when you want to view the results right in R

library(stargazer)
###############Model 1 
Model.1<-lm(Memory~ Practice, data = CorrDataT)
###############Model 2
Model.2<-lm(Memory~ Practice+Anxiety, data = CorrDataT)
stargazer(Model.1,Model.2,type="latex",
          intercept.bottom = FALSE, single.row=TRUE, 
          star.cutoffs=c(.05,.01,.001), notes.append = FALSE,
          header=FALSE)

Plots

• Now piloting it a bit more complex as we have two predictors
• Simple scatter plots are not semi-partialed
• Also while we are not interacting the two variables, each has an effect on the DV
• We must visualize both effects
• There are different suggestions on how to do this [we will come back to differences in plotting later]

library(effects)
#plot individual effects
Model.2.Plot <- allEffects(Model.2, 
                           xlevels=list(Practice=seq(8, 12, 1),
                                        Anxiety=seq(8, 12, 1)))

plot(Model.2.Plot, 'Practice', ylab="Memory")
plot(Model.2.Plot, 'Anxiety', ylab="Memory")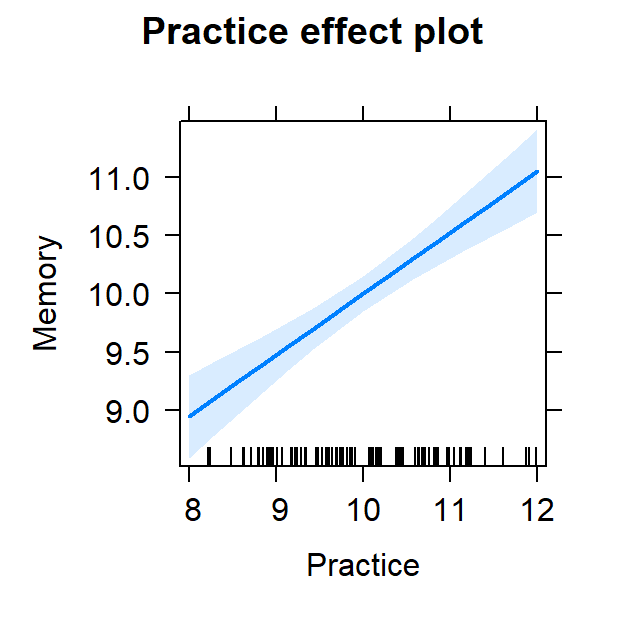

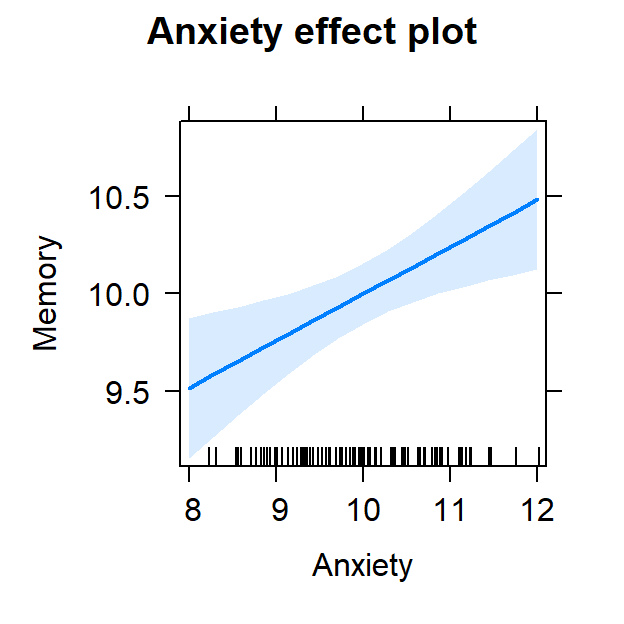
Fully Indrect

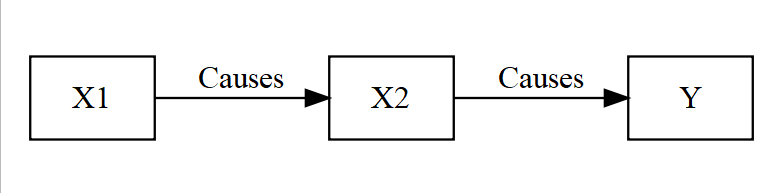
• Not spurious, but X1 is not direct to Y (X2 is intervening completely)

Full Redundancy (Spurious models)

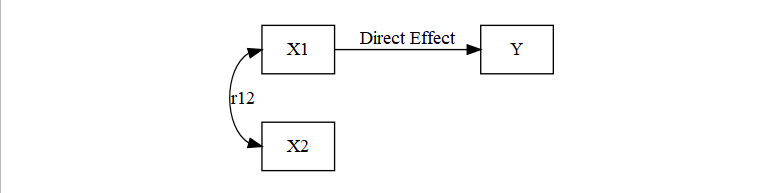
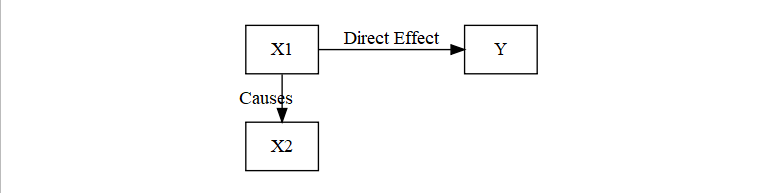
• Happens when, \(r_{Y2} \approx r_{Y1}r_{12}\)
• X1 is confounded in X2
  • X1 and X2 are redundant

Example of Full Redundancy

I.py1 =.6 #Cor between X1 (Working Memory Digit Span) and Memory Errors
I.py2 =.6 #Cor between X2 (Auditory Working Memory) and Memory Errors
I.p12 =.9999 #Cor between X1 Working Memory and Auditory Working Memory 

I.Means.X1X2Y<- c(10,10,10) #set the means of X and Y variables
I.CovMatrix.X1X2Y <- matrix(c(1,I.p12,I.py1,
                            I.p12,1,I.py2,
                            I.py1,I.py2,1),3,3) # creates the covariate matrix 
set.seed(42)
IData<-mvrnorm(n=100, mu=I.Means.X1X2Y,Sigma=I.CovMatrix.X1X2Y, empirical=TRUE)
IData<-as.data.frame(IData)
#lets add our labels to the vectors we created
colnames(IData) <- c("WM","AWM","Errors")

###############Model 1 
Spurious.1<-lm(Errors~ WM, data = IData)
###############Model 2 
Spurious.2<-lm(Errors~ AWM, data = IData)
###############Model 3
Spurious.3<-lm(Errors~ WM+AWM, data = IData)
stargazer(Spurious.1,Spurious.2,Spurious.3,type="latex",
          intercept.bottom = FALSE, single.row=TRUE, 
          star.cutoffs=c(.05,.01,.001), notes.append = FALSE,
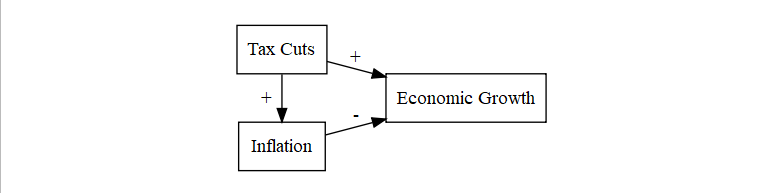
          header=FALSE)

Suppression

• Suppression is a strange case where the IV -> DV relationship is hidden (suppressed) by another variable
• Tax cuts cause growth, tax cuts cause inflation. Tax cuts alone might look +, but add in inflation and now tax cuts could make cause the growth to look different
• Or the the suppressor variable can cause a flip in the sign of the relationship

Hidden Effect Example

sup.py1 =  2.5 #Covar between tax cuts and growth 
sup.py2 = -5.5 #Covar between inflation and growth 
sup.p12 =  4  #Covar between tax cuts and inflation
Supp.X1X2Y<- c(5,5,5) #set the means of X and Y variables
Supp.CovMatrix.X1X2Y <- matrix(c(10,sup.p12,sup.py1,
                                 sup.p12,10,sup.py2,
                                 sup.py1,sup.py2,10),3,3) # creates the covariate matrix 
set.seed(42)
SuppData<-mvrnorm(n=100, mu=Supp.X1X2Y,Sigma=Supp.CovMatrix.X1X2Y, empirical=TRUE)
SuppData<-as.data.frame(SuppData)
colnames(SuppData) <- c("TaxCuts","inflation","growth")

###############Model 1 
TaxCutsOnly<-(lm(growth~ TaxCuts, data = SuppData))
###############Model 2
Full.Model<-lm(growth~ TaxCuts+inflation, data = SuppData)
stargazer(TaxCutsOnly,Full.Model,type="latex",
          intercept.bottom = FALSE, single.row=TRUE, 
          star.cutoffs=c(.05,.01,.001), notes.append = FALSE,
          header=FALSE)

• You will notice tax cuts alone, 0.25, was lower than 0.56 controlling for inflation.
• However, you will notice inflation,-0.774, has a bigger effect (and negative) effect than tax cuts 0.56
• So in other words, yes tax cuts work but they don’t override inflation!

Plot predictions

• Also how you plot depends on your theory/experiment/story
• We need to control for inflation (or view tax slope at different levels of inflation)
• First lets view the tax slope without controlling for inflation

#plot individual effects
Tax.Model.Plot <- allEffects(TaxCutsOnly, 
                             xlevels=list(TaxCuts=seq(3, 7, 1)))
plot(Tax.Model.Plot, 'TaxCuts', ylab="Growth")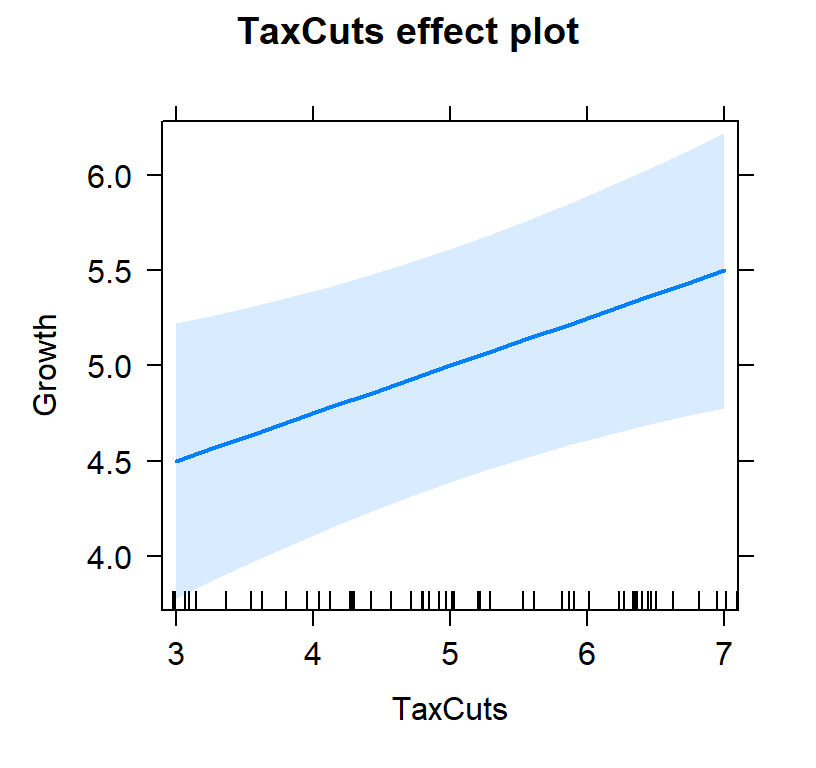

• Now lets view it controlling for inflation

#plot individual effects
Full.Model.Plot <- allEffects(Full.Model, 
                              xlevels=list(TaxCuts=seq(3, 7, 1),
                                           inflation=seq(3, 7, 1)))
plot(Full.Model.Plot, 'TaxCuts', ylab="Growth")
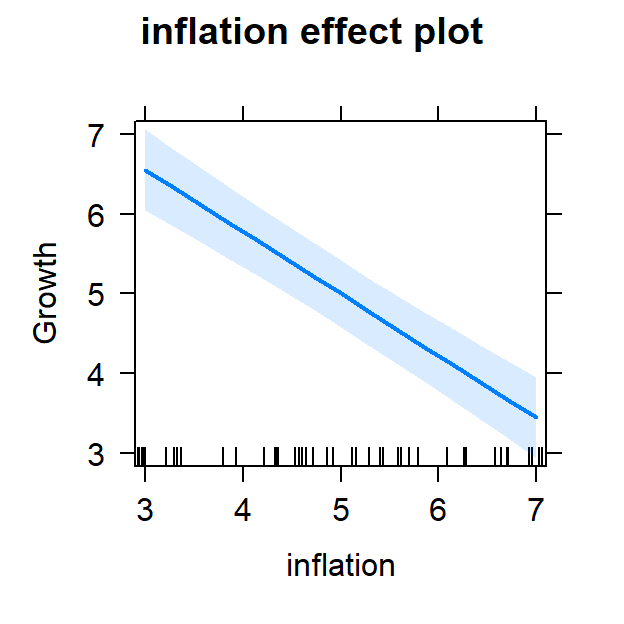
plot(Full.Model.Plot, 'inflation', ylab="Growth")

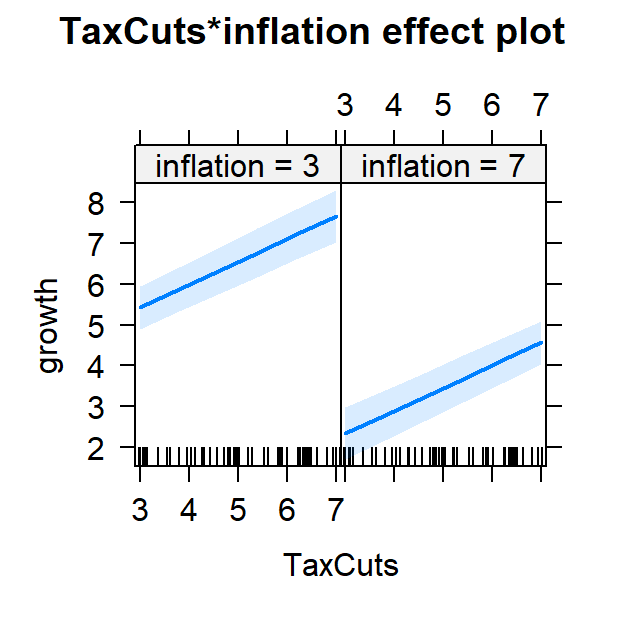
#plot both effects
Full.Model.Plot2<-Effect(c("TaxCuts", "inflation"), Full.Model,
                         xlevels=list(TaxCuts=c(3, 7), 
                                      inflation=c(3,7)))
plot(Full.Model.Plot2)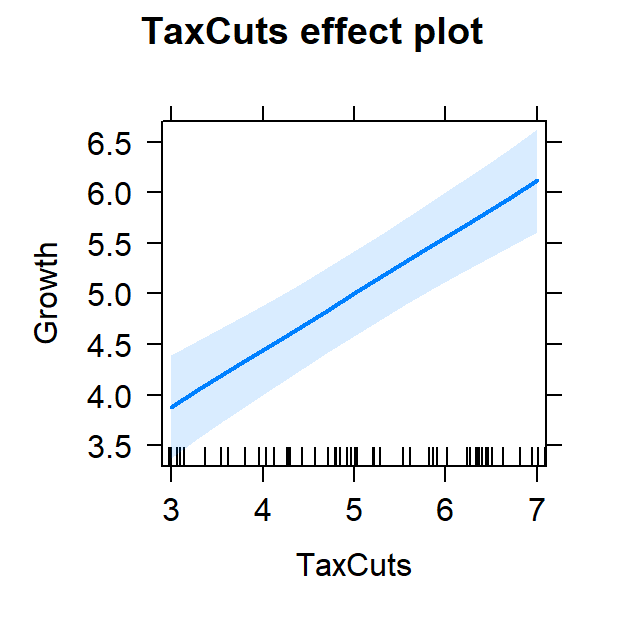

Estimating population R-squared

• \(\rho^2\) is estimated by multiple \(R^2\)
• Problem: in small samples correlations are unstable (and inflated)
• Also, as we add predictors, \(R^2\) gets inflated
• So we use an adjusted multiple \(R^2\)
• Adjusted \(R^2 = 1 - 1- R_Y^2 \frac{n-1}{n-k-1}\)

Multiple Linear Regression Assumptions

• Multicollinearity: Predictors cannot be fully (or nearly fully) redundant [check the correlations between predictors]
• Homoscedasticity of residuals to fitted values
• Normal distribution of residuals
• Absence of outliers
• Ratio of cases to predictors
  • Number of cases must exceed the number of predictors
  • Barely acceptable minimum: 5 cases per predictor
  • Preferred minimum: 20-30 cases per predictor
• Linearity of prediction
• Independence (no auto-correlated errors)

How to check assumptions?

• First lets fit the model

Linear.Model<-lm(Memory~ Practice+Anxiety, data = CorrDataT)

Lets test for Multicollinearity

• Multicollinearity can be detected when the variance on the terms you are interested in become inflated
• So we need to test the variance on the factors.
• Basic Logical step 1) get Variance on predictor (only that term in model) [Vmin]
• Basic Logical step 2) get Variance (Vmax) on predictor (all other terms in model) [Vmax]
• Basic Logical step 3) ratio: Vmax/Vmin. if the value > 4 you have a problem
• that’s alot of steps. R can do it for you basically with one line of code
• Variance inflation factors (vif)

library(car)
vif(Linear.Model) # variance inflation factors 

## Practice  Anxiety 
## 1.098901 1.098901

vif(Linear.Model) > 4 # problem?

## Practice  Anxiety 
##    FALSE    FALSE

lets check normality, outlinears visually first

#To see them all at once
layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page 
plot(Linear.Model)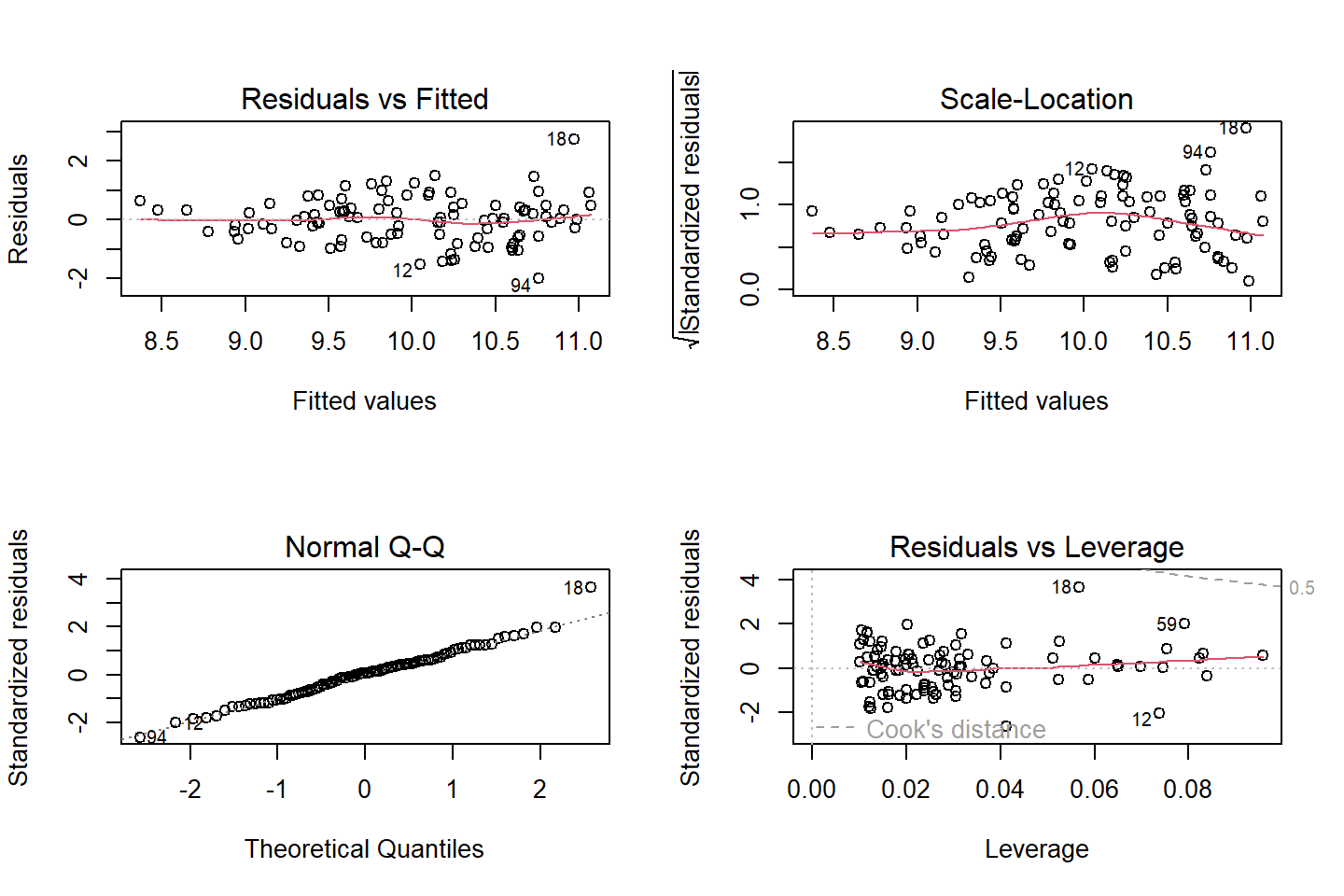

Residuals vs fitted and sqaure-rooted residuals vs fitted

• should be Homoscedastistic (randomly distributed around 0)
• There is statistical test (in R, but not SPSS)

# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(Linear.Model)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 6.705913, Df = 1, p = 0.0096094

Q-Q plot

• should be a straight line
• you can also visualize the residuals as a histogram

# distribution of studentized residuals
sresid <- studres(Linear.Model) 
hist(sresid, freq=FALSE, 
     main="Distribution of Studentized Residuals")
xfit<-seq(min(sresid),max(sresid),length=40) 
yfit<-dnorm(xfit) 
lines(xfit, yfit)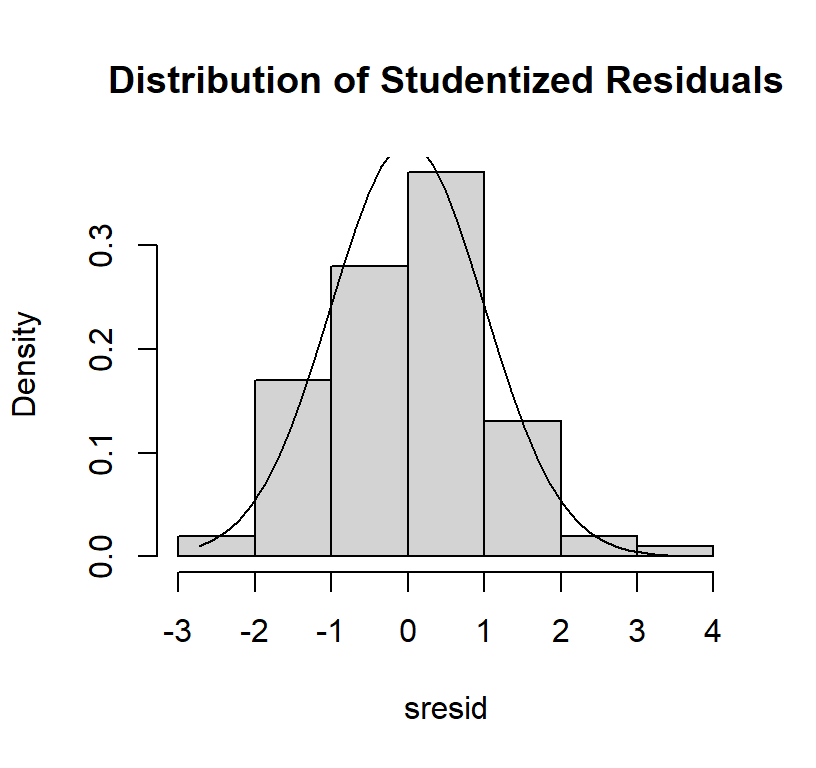

Cook’s distances

• Its possible for one or more observations to “pull” the regression line away from the trend in the rest of the data
• Cook’s Distance is one of several possible measures of influence.
• Cook’s D is the sum of the differences between the predicted value and the other predicted values in the data set, divided by the error variance times the number of parameters in the model.
• R did this automatically in plot 4 and we can see a few people with numbers (those are the outliers)
• We can also see the influence with a little R coding (set a more conservative threshold)

# Cook's D plot
# identify D values > 4/(n-k-1) 
cutoff <- 4/((nrow(CorrDataT)-length(Linear.Model$coefficients)-2)) 
cutoff

## [1] 0.04210526

plot(Linear.Model, which=4, cook.levels=cutoff)
plot(Linear.Model, which=5, cook.levels=cutoff)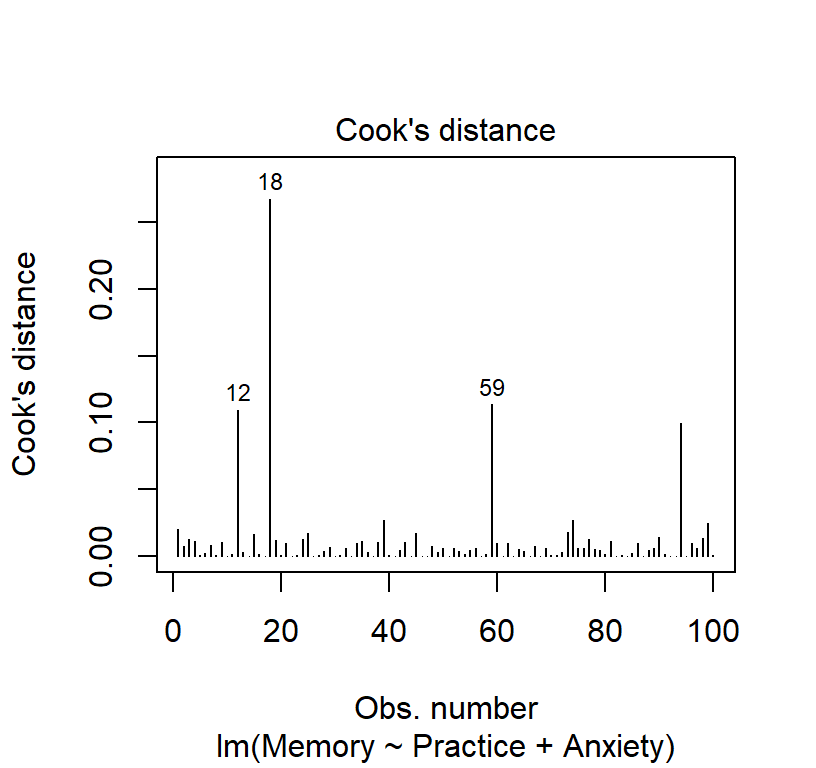

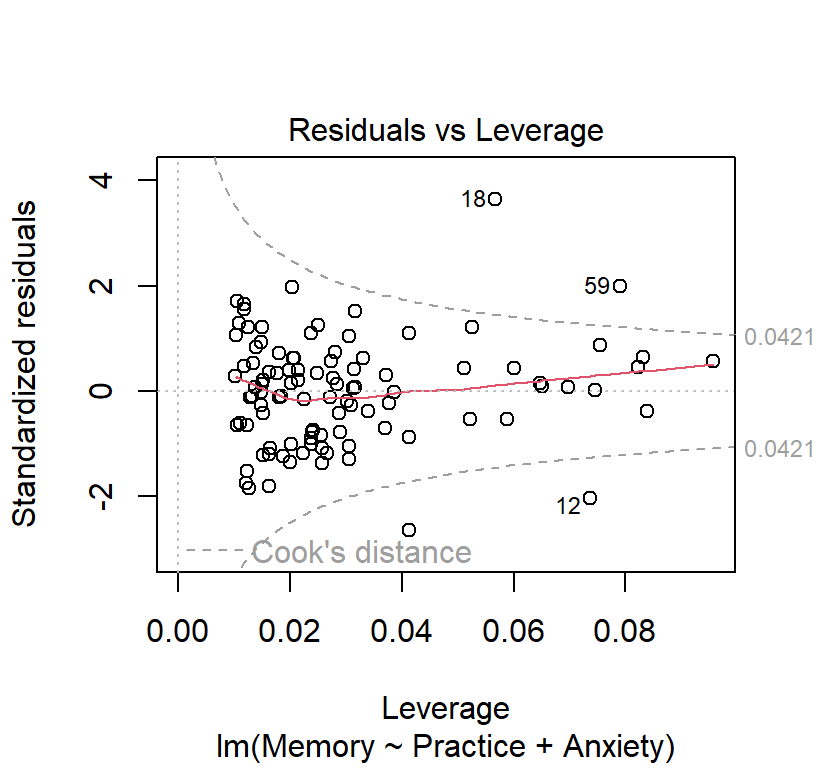
• Remove those with large Cooks’ Distances (if we want too)

CorrDataT$CooksD<-(cooks.distance(Linear.Model))
CorrDataT_Cleaned<-subset(CorrDataT,CooksD < cutoff)
nrow(CorrDataT_Cleaned)

## [1] 96

Another method of testing for influence

• Bonferonni p-value for most extreme obs
• Notice it gives different number of outliers
• Not all tests agree

# Assessing Outliers
outlierTest(Linear.Model) # Bonferonni p-value for most extreme obs

##    rstudent unadjusted p-value Bonferroni p
## 18 3.906991         0.00017396     0.017396

Linearity and autocorrelation tests

• Green lines should show straight lines relative to the red dotted line
• The auto-correlation test should be non-significant (means that each residual is not correlated to the next residual)

# Evaluate Nonlinearity
# component + residual plot aka partial-residual plots
crPlots(Linear.Model)
# Test for Autocorrelated Errors
durbinWatsonTest(Linear.Model)

##  lag Autocorrelation D-W Statistic p-value
##    1      0.08884707      1.814168   0.356
##  Alternative hypothesis: rho != 0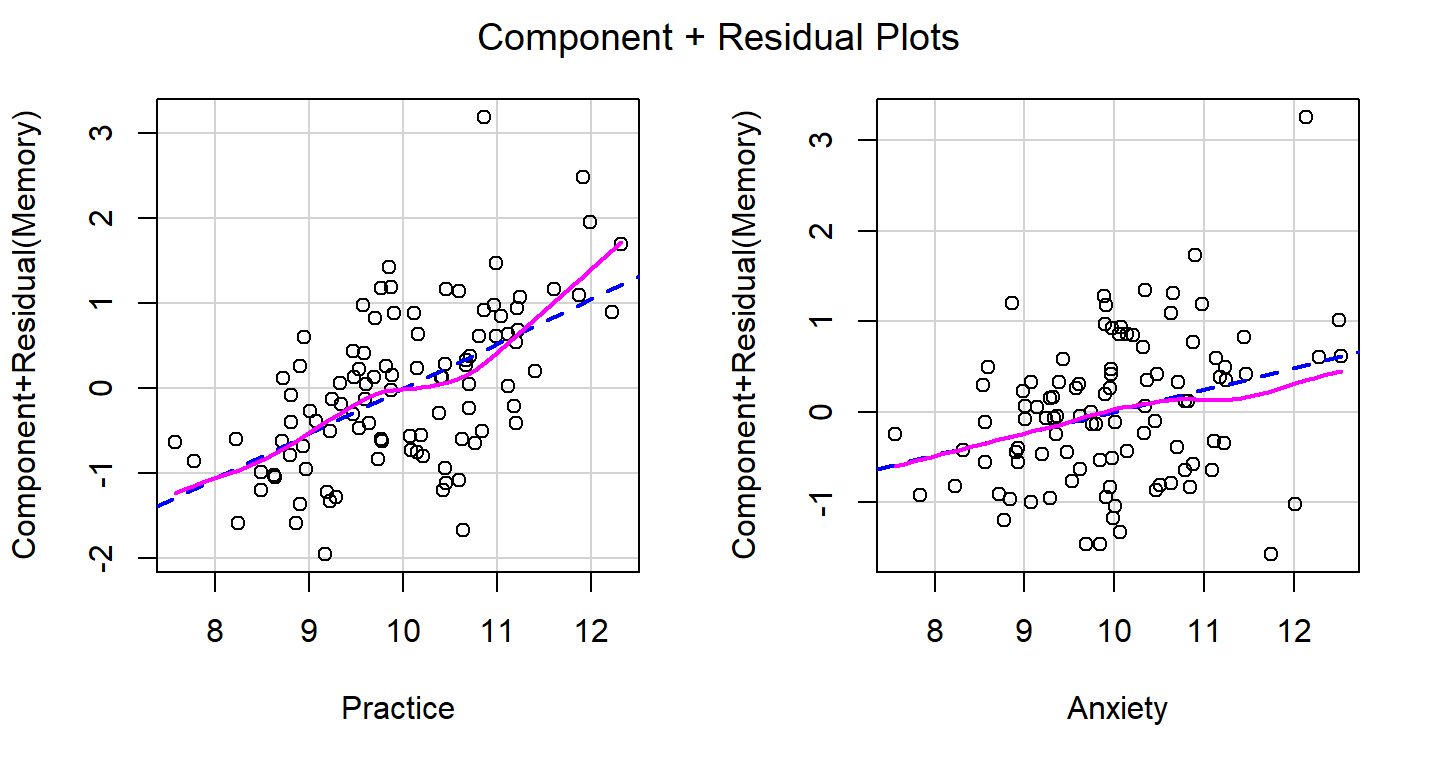

Save the results of modeling

• This lets you make a Doc file

library(texreg)
#htmlreg(list(Linear.Model),file = "ModelResults.doc", 
#        single.row = FALSE, stars = c(0.001, 0.01, 0.05,0.1),digits=3,
#        inline.css = FALSE, doctype = TRUE, html.tag = TRUE, 
#        head.tag = TRUE, body.tag = TRUE)