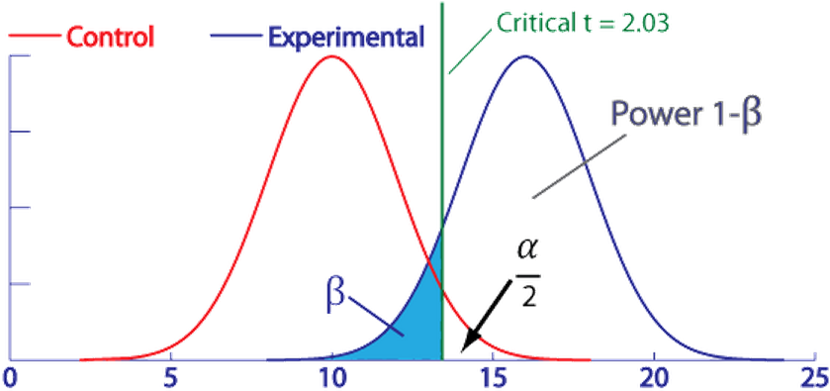
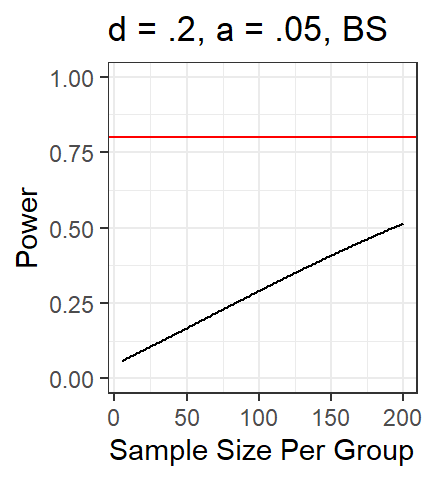
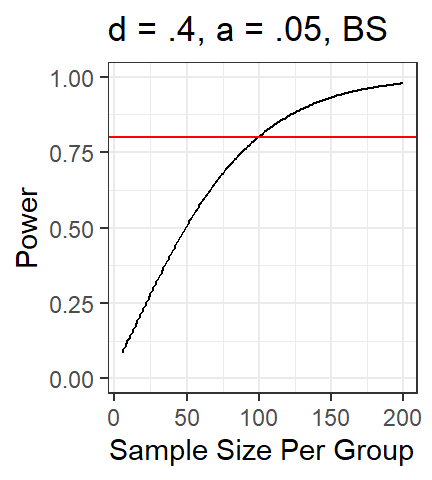
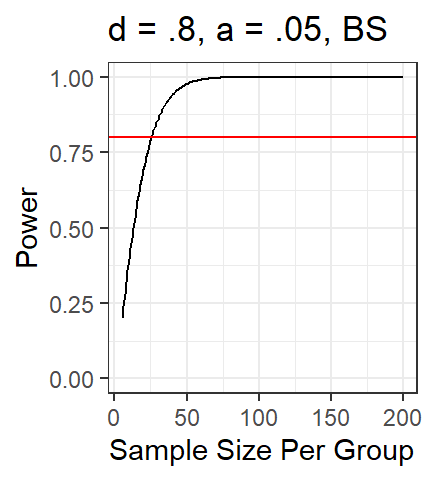
Simulation-based approach
- R allows for the Monte-Carlo method, repeated simulations based on
assumptions to find solutions
- Here is a Monte-Carlo solution to t-test power, where I assume each
group follows a normal distribution
MC.ttest <-function(Params) {
TrueD<-Params[[1]]; alpha<-Params[[2]]
N1<-Params[[3]]; N2<-Params[[4]]
# Set distrobutions
Control<-rnorm(N1, mean = 0, sd = 1)
Exp<-rnorm(N2, mean = TrueD, sd = 1)
# Run t-est
calcP<-t.test(Exp,Control,
alternative = c("two.sided"),
paired = FALSE, var.equal = TRUE,
conf.level = 1-alpha)$p.value
result<-calcP
return(result)
}
# Paramaters
d = .8; alpha= .05; N1=20; N2=20; Sim=1000
# Run simulation
Pvalues<-replicate(Sim,MC.ttest(c(d,alpha,N1,N2)))
Sig<-ifelse(Pvalues <= alpha, 1, 0)
PowerMC<-sum(Sig)/Sim
Simulated Power = 0.718 which should be very close to a formula
solution 0.6934042
- We would have to build simulations like this for each and every
design we wanted to test and for mixed models, this is a lot of
programming!
Simr package
- Simr package makes it easier to do this kind of simulations
- The package is not well documented and its sort of buggy (but so far
its easiest to use)
- You can use it construct a simulation based on parameters (like
Westfall et al.), but it simulates the power or you can base it on a
previous model
Simulation from Parameters
- Let’s redo our experiment from above
- This is basically going to give an observed power
- Start by specifying the number of subjects (n = 30) and
items (n = 10)
library(simr)
Item <- as.factor(rep(1:10))
Subject <- as.factor(rep(1:30))
Condition1<-rep(-.5:.5)
# creates "frame" for our data
X <- expand.grid(Subject=Subject,Item=Item, Condition1=Condition1)
|
Subject
|
Item
|
Condition1
|
|
1
|
1
|
-0.5
|
|
2
|
1
|
-0.5
|
|
3
|
1
|
-0.5
|
|
4
|
1
|
-0.5
|
|
5
|
1
|
-0.5
|
|
6
|
1
|
-0.5
|
- Next, we need to specify (we will set the random correlation to be
zero for now)
- Fixed terms
- Intercept & Condition [intercept = 10.19, Fixed slope of C1 =
4.77] -Random terms (C1 is a slope [effects coded] -.5,.5)
- If we did this (1+C1|Subjects) our COV matrix would look like
this:
\[
\mathbf{COV: Subj} = \left[\begin{array}
{rrr}
Intercept & cov(IxSlope) \\
cov(IxSlope) & Slope \\
\end{array}\right]
\]
- For Subjects we will do (assume 0 correlation between
intercept/slope)
\[
\mathbf{Subject} = \left[\begin{array}
{rrr}
23.47 & 0 \\
0 & 3.98 \\
\end{array}\right]
\]
- For Items we will do (assume 0 correlation between
intercept/slope)
\[
\mathbf{Items} = \left[\begin{array}
{rrr}
2.197 & 0 \\
0 & 5.009 \\
\end{array}\right]
\]
- Setup our simulations to let the correlations vary around zero:
# fixed intercept and slope
b <- c(10.1912, 4.7773)
# random intercept and slope variance-covariance matrix
# For Subject
SubVC <-matrix(c(23.471,0,0,3.98), 2)
# For Items
ItemVC <- matrix(c(2.197,0,0,5.009), 2)
# Exrtact the residual sd
s <- 7.13^.5
- Next, we need to make a lmer object
- we need to feed in the fixed effects, random effects, residual, and
“frame” of the data
SimModel <- makeLmer(DV ~ Condition1 + (Condition1|Subject)+(Condition1|Item),
fixef=b, VarCorr=list(SubVC,ItemVC), sigma=s, data=X)
summary(SimModel)
## Linear mixed model fit by REML ['lmerMod']
## Formula: DV ~ Condition1 + (Condition1 | Subject) + (Condition1 | Item)
## Data: X
##
## REML criterion at convergence: 3516.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.1451 -0.6925 0.0210 0.7147 3.9010
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## Subject (Intercept) 23.471 4.845
## Condition1 3.980 1.995 0.00
## Item (Intercept) 2.197 1.482
## Condition1 5.009 2.238 0.00
## Residual 7.130 2.670
## Number of obs: 600, groups: Subject, 30; Item, 10
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 10.1912 1.0070 10.121
## Condition1 4.7773 0.8253 5.789
##
## Correlation of Fixed Effects:
## (Intr)
## Condition1 0.000
- You will notice the SimModel looks like our real data
- This is the model it is going to parametrically simulate
- Here is an example of 1 dataset it will simulate given these
parameters
kable(head(getData(SimModel))) %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"))
|
Subject
|
Item
|
Condition1
|
DV
|
|
1
|
1
|
-0.5
|
-12.437575
|
|
2
|
1
|
-0.5
|
-4.208957
|
|
3
|
1
|
-0.5
|
-12.357406
|
|
4
|
1
|
-0.5
|
16.627996
|
|
5
|
1
|
-0.5
|
-6.136707
|
|
6
|
1
|
-0.5
|
16.740027
|
Plot
- One simulation from simr package based on our parameters
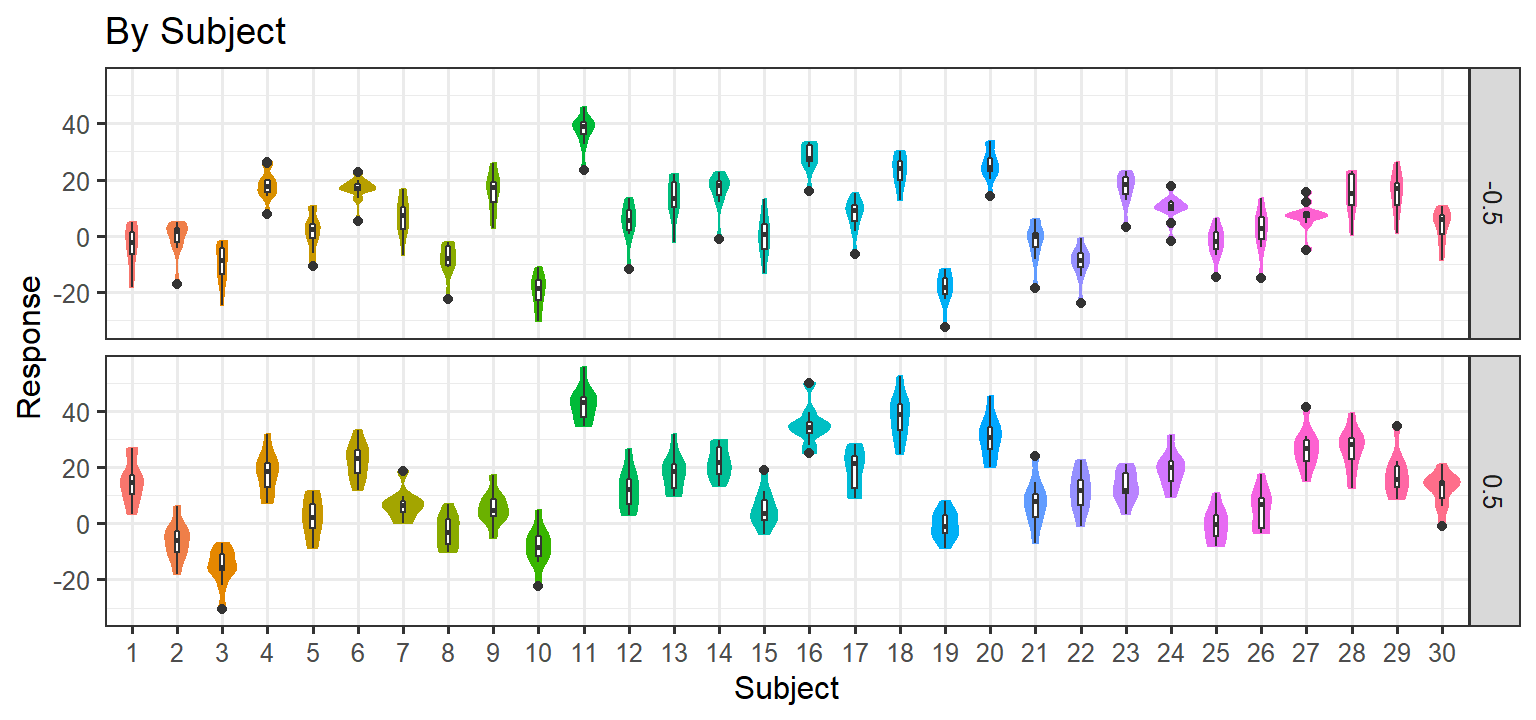
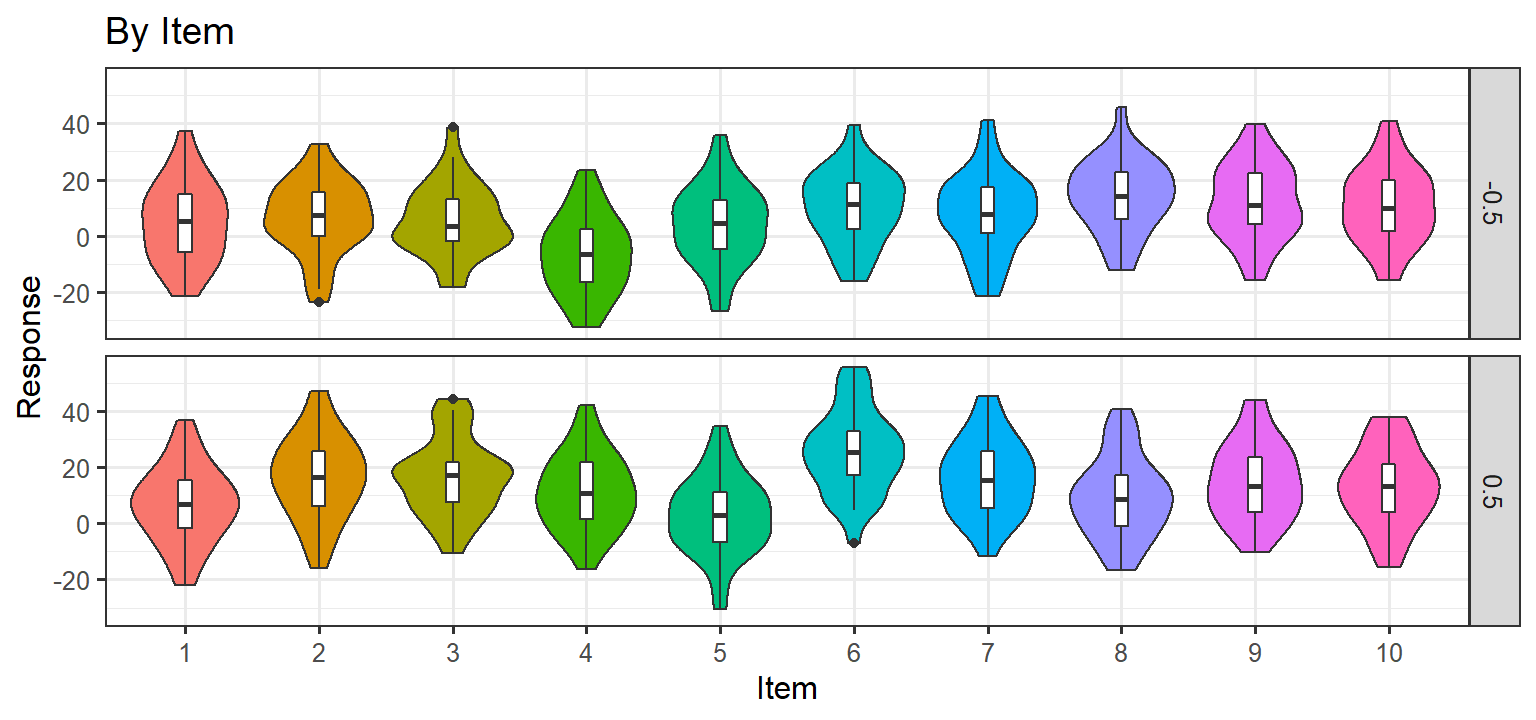
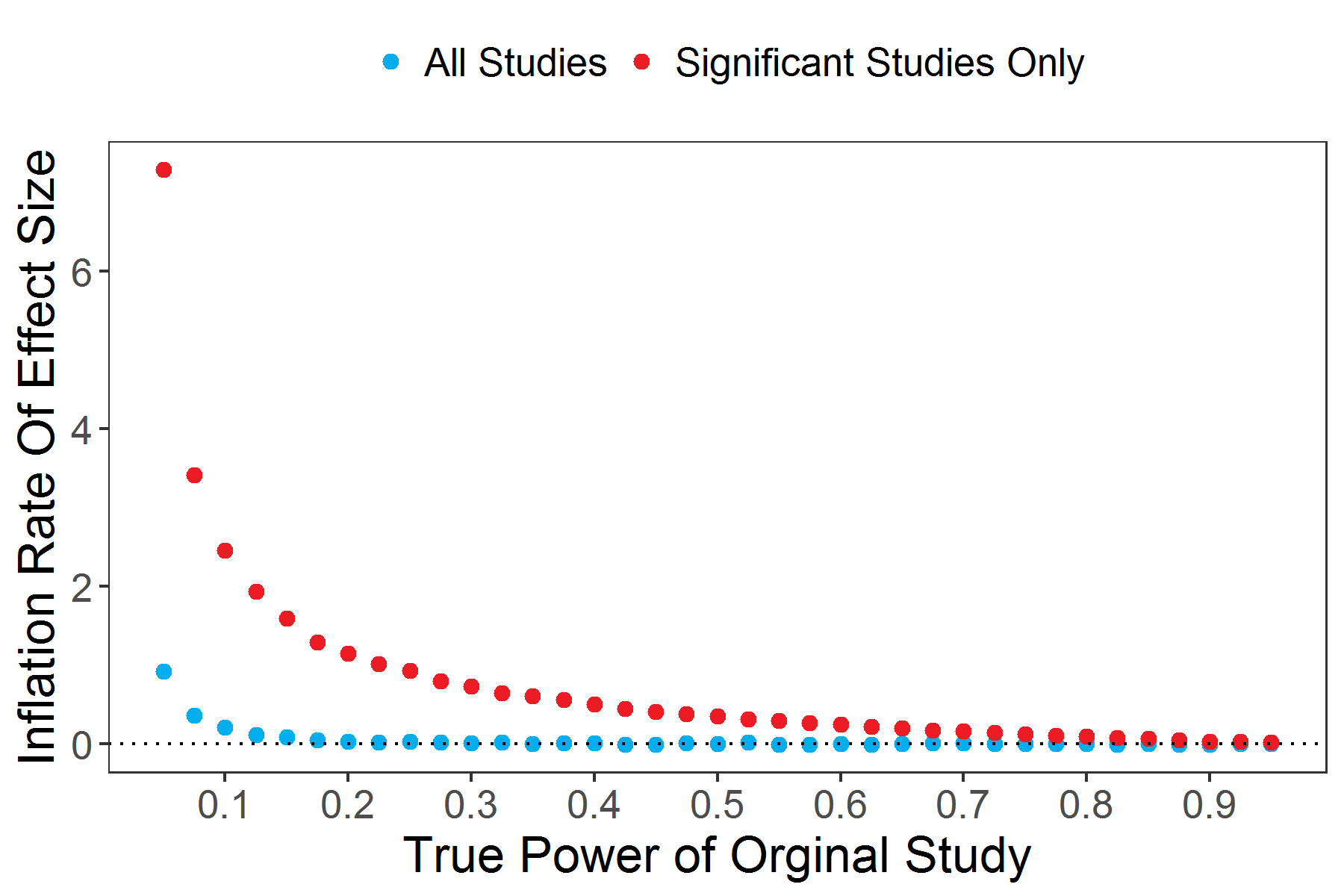
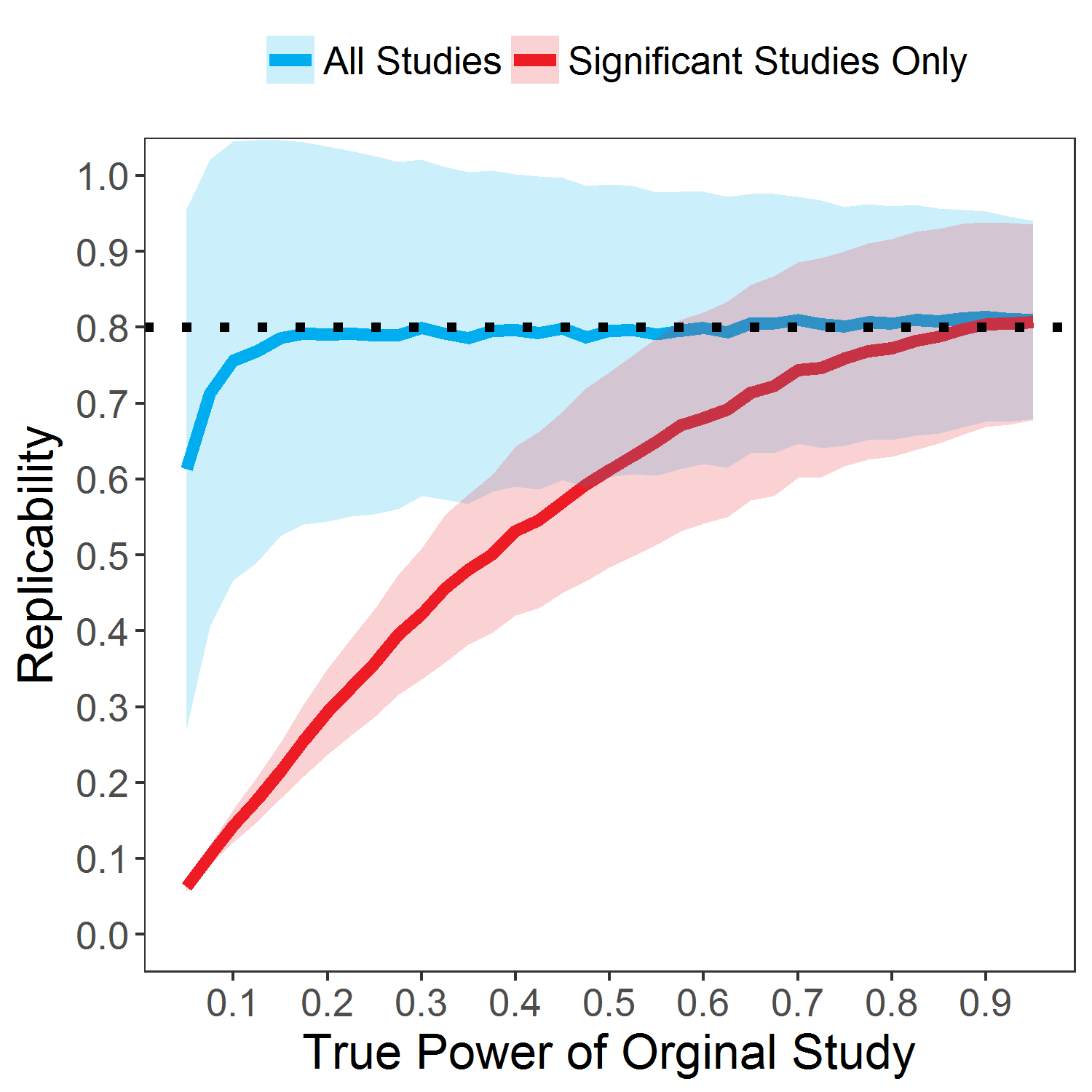
Monte-Carlo Simulation
- What we want to do is simulate this 100 times to keep the
computational time short (but 1000 is the default)
- But we need to figure out what we want to test about our model and
how
- We want to test fixed or random effects? Let’s just worry about
fixed
- Which pvalues do we want to use?
- z, t, F scores (z,t,f), Likelihood ratio test (lr), Kenward-Roger
(kr), or Parametric bootstrap (pb)?
- I will tell it to give me the observed power for the fixed effect of
Condition using lr method (to be faster, but with an alpha .045, since
we have seen in the last few weeks that Likelihood ratio testing tends
to yield type I error slighly above .05)
SimPower1<-powerSim(SimModel,fixed("Condition1", "lr"),
nsim=100, alpha=.045, progress=FALSE)
SimPower1
## Power for predictor 'Condition1', (95% confidence interval):
## 100.0% (96.38, 100.0)
##
## Test: Likelihood ratio
## Effect size for Condition1 is 4.8
##
## Based on 100 simulations, (8 warnings, 0 errors)
## alpha = 0.045, nrow = 600
##
## Time elapsed: 0 h 0 m 22 s
- Obviously, we have high power, because this is Observed
Power
Using VPC over raw scores
- We can use our VPC measures we calculated and get the same
answer
b2 <- c(0, d.mixed) # fixed intercept and slope
SubVC2 <-matrix(c(.5616,0,0,.09527), 2)
ItemVC2 <- matrix(c(.05256,0,0,.11984), 2)
s2 <- (.1707)^.5 # residual sd
SimVPC <- makeLmer(DV ~ Condition1 + (Condition1|Subject)+(Condition1|Item),
fixef=b2, VarCorr=list(SubVC2,ItemVC2), sigma=s2, data=X)
SimPower.VPC<-powerSim(SimVPC,fixed("Condition1", "lr"),
nsim=100, alpha=.045, progress=FALSE)
SimPower.VPC
## Power for predictor 'Condition1', (95% confidence interval):
## 100.0% (96.38, 100.0)
##
## Test: Likelihood ratio
## Effect size for Condition1 is 0.74
##
## Based on 100 simulations, (1 warning, 0 errors)
## alpha = 0.045, nrow = 600
##
## Time elapsed: 0 h 0 m 22 s
Block correlations in Model Fitting
- To block he correlations we need to write them out differently
b2 <- c(0, d.mixed) # fixed intercept and slope
SubVC2a <-.5616
SubVC2b <-.09527
ItemVC2a <-.05256
ItemVC2b <-.11984
s2 <- (.1707)^.5 # residual sd
SimVPCa <- makeLmer(DV ~ Condition1 + (Condition1||Subject)+(Condition1||Item),
fixef=b2, VarCorr=list(SubVC2a,SubVC2b,ItemVC2a,ItemVC2b), sigma=s2, data=X)
SimPower.VPCa<-powerSim(SimVPCa,fixed("Condition1", "lr"),
nsim=100, alpha=.045, progress=FALSE)
SimPower.VPCa
## Power for predictor 'Condition1', (95% confidence interval):
## 100.0% (96.38, 100.0)
##
## Test: Likelihood ratio
## Effect size for Condition1 is 0.74
##
## Based on 100 simulations, (1 warning, 0 errors)
## alpha = 0.045, nrow = 600
##
## Time elapsed: 0 h 0 m 17 s
Simulate Observed Power Directly
- You can simply call the model we analyzed and it will work
SimPower.Direct<-powerSim(MaxModel,fixed("Condition1", "lr"),
nsim=100, alpha=.045, progress=FALSE)
SimPower.Direct
## Power for predictor 'Condition1', (95% confidence interval):
## 100.0% (96.38, 100.0)
##
## Test: Likelihood ratio
## Effect size for Condition1 is 4.8
##
## Based on 100 simulations, (3 warnings, 0 errors)
## alpha = 0.045, nrow = 1200
##
## Time elapsed: 0 h 0 m 15 s
##
## nb: result might be an observed power calculation
- Since the program notices you are calling from real data its warning
you that this may be observed power.
Power Curve
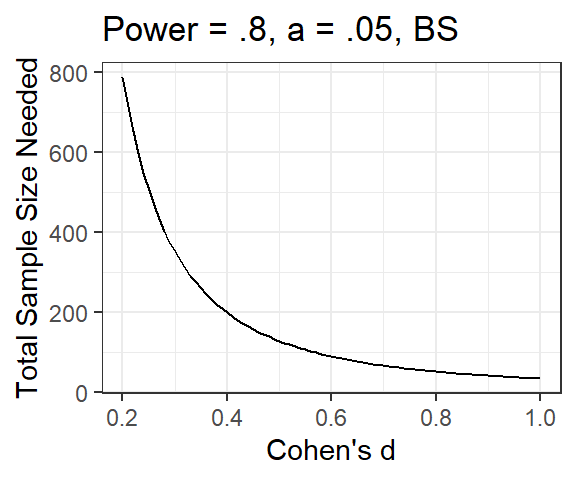
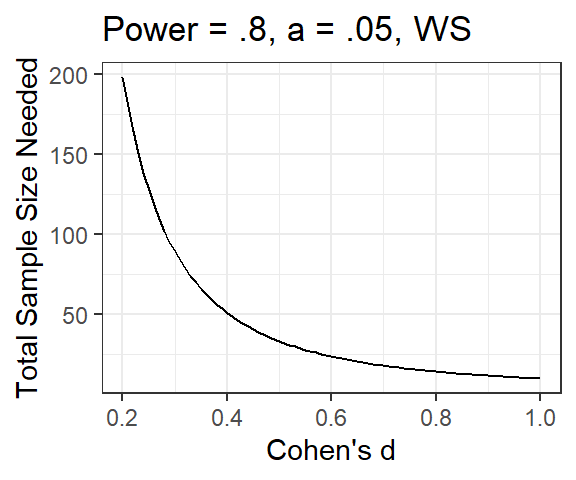
- Lets say we need to figure out how many subjects or items we would
want to collect for a future study based on our pilot study?
- What we need to do is resimulate our experiments, but expand out the
number of subjects or items
- Basically we have to change the sample size (of items or subjects)
and run a monte-carlo simulation each time. So based on the number of
sample sizes you want to test
- This is very computationaly expensive (Slow)
- Take the second example from Brysbaert & Stevens, 2018
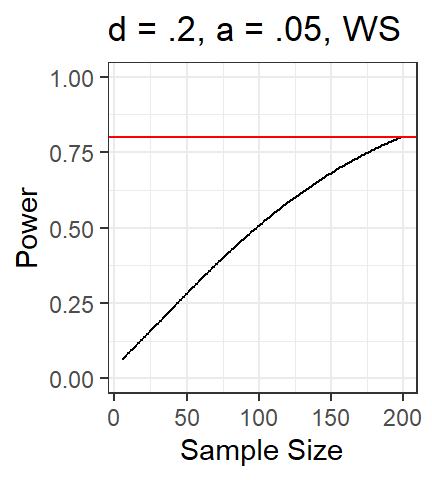
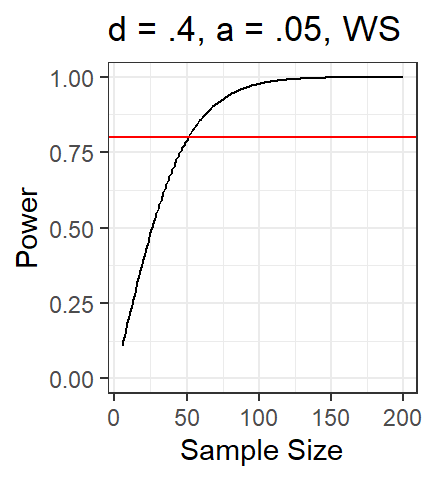
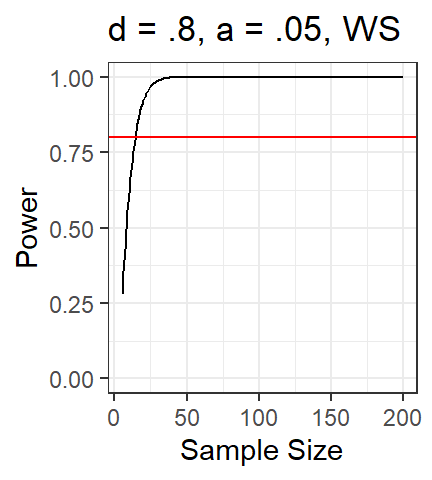
- Let’s first just do subjects
- n = 20, 40, 60, 80 [so our simulated data set must be built
with N = 80]
- 20 items
- alpha =.045 (lr testing)
- d = .112
Item <- as.factor(rep(1:20))
Subject <- as.factor(rep(1:80))
Condition1<-rep(-.5:.5)
X <- expand.grid(Subject=Subject,Item=Item, Condition1=Condition1)
b2 <- c(0, .112)
SubVC2 <-matrix(c(.368,0,0,.004), 2)
ItemVC2 <- matrix(c(.068,0,0,.001), 2)
s2 <- (.559)^.5 # residual sd
SimCurve <- makeLmer(DV ~ Condition1 + (Condition1|Subject)+(Condition1|Item),
fixef=b2, VarCorr=list(SubVC2,ItemVC2), sigma=s2, data=X)
summary(SimCurve)
## Linear mixed model fit by REML ['lmerMod']
## Formula: DV ~ Condition1 + (Condition1 | Subject) + (Condition1 | Item)
## Data: X
##
## REML criterion at convergence: 7542.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.0709 -0.6601 0.0064 0.6785 3.1029
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## Subject (Intercept) 0.368 0.60663
## Condition1 0.004 0.06325 0.00
## Item (Intercept) 0.068 0.26077
## Condition1 0.001 0.03162 0.00
## Residual 0.559 0.74766
## Number of obs: 3200, groups: Subject, 80; Item, 20
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 0.00000 0.09041 0.000
## Condition1 0.11200 0.02826 3.963
##
## Correlation of Fixed Effects:
## (Intr)
## Condition1 0.000
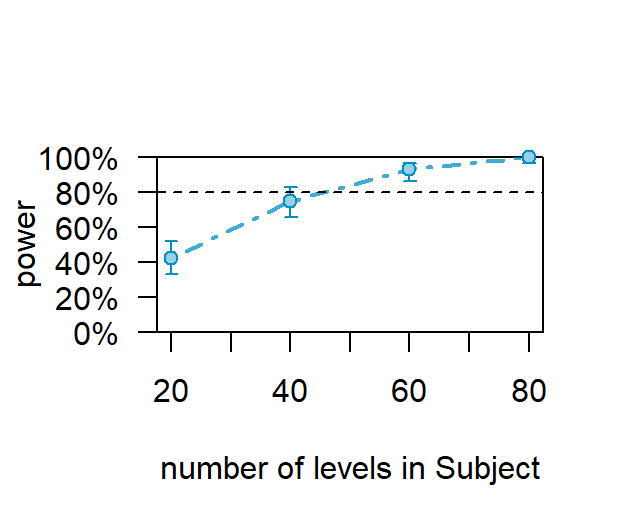
- Using the powerCurve function we can test across
subjects
SCurve1<-powerCurve(SimCurve, fixed("Condition1", "lr"),
along = "Subject",
breaks = c(20,40,60,80),
nsim=100,alpha=.045, progress=FALSE)
plot(SCurve1)
- Test across items, which will calculate for 80 subects, so examine
less items
SCurve2<-powerCurve(SimCurve, fixed("Condition1", "lr"),
along = "Item",
breaks = c(5,10,15),
nsim=100,alpha=.045, progress=FALSE)
plot(SCurve2)
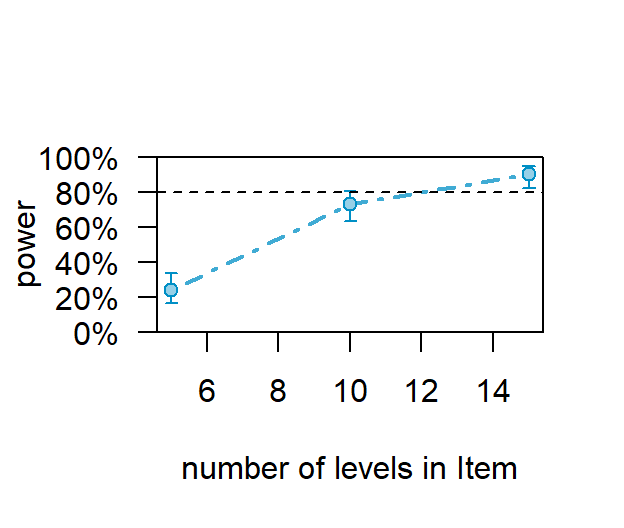
- Using these same parameters (N = 80, Items = 20) Westfall website
yielded a power of .894. The simulation suggested power of 95%, with a
CI = [88.72 - 98.36]. So they seem to agree in this case (but they did
not agree with our first example, but that effect size was huge)
Simulate higher order interactions
- You can simulate more complex models and more complex terms, but you
must map out the matrix more carefully
- You have to estimate fixed slopes (C1 + C2 + C1:C1)
- You have to predefine all your random effects
- if we assume
- For simplicity we can assume zero random correlations using
diag command.
- subject diag(intercept, C1 slope, C2 slope, C1:C2 slope)
Item <- as.factor(rep(1:20))
Subject <- as.factor(rep(1:20))
C1<-rep(-.5:.5)
C2<-rep(-.5:.5)
# creates "frame" for our data
X <- expand.grid(Subject=Subject,Item=Item, C1=C1,C2=C2)
b3 <- c(0, .05,-.05,.1) # fixed intercept and slope
SubVC3 <-diag(c(.35,.005,.005,.005))
ItemVC3 <-diag(c(.1,.005,.005,.005)) # random intercept and slope variance-covariance matrix
s3 <- (1-(sum(SubVC3)+sum(ItemVC3)))^.5 # residual sd
SimInter <- makeLmer(DV ~ C1*C2 + (C1*C2|Subject)+(C1*C2|Item),
fixef=b3, VarCorr=list(SubVC3,ItemVC3), sigma=s3, data=X)
summary(SimInter)
SimPower.Inter<-powerSim(SimInter,fixed("C1:C2", "lr"),
nsim=100, alpha=.045, progress=FALSE)
SimPower.Inter
References
Brysbaert, M., & Stevens, M. (2018). Power analysis and effect
size in mixed effects models: A tutorial. Journal of Cognition,
1(1).
Fischer, P., Krueger, J. I., Greitemeyer, T., Vogrincic, C.,
Kastenm?ller, A., Frey, D., … & Kainbacher, M. (2011). The
bystander-effect: a meta-analytic review on bystander intervention in
dangerous and non-dangerous emergencies. Psychological
bulletin, 137(4), 517.
Green, P., & MacLeod, C. J. (2016). SIMR: an R package for power
analysis of generalized linear mixed models by simulation. Methods
in Ecology and Evolution, 7(4), 493-498.
Hoenig, J.M. & Heisey, D.M. (2001) The abuse of power: the
pervasive fallacy of power calculations for data analysis. The
American Statistician, 55, 19-24.
Judd, C. M., Westfall, J., & Kenny, D. A. (2017). Experiments
with more than one random factor: Designs, analytic models, and
statistical power. Annual Review of Psychology, 68,
601-625.
Westfall, J., Kenny, D. A., & Judd, C. M. (2014). Statistical
power and optimal design in experiments in which samples of participants
respond to samples of stimuli. Journal of Experimental Psychology:
General, 143(5), 2020-2045.
LS0tDQp0aXRsZTogJ1Bvd2VyIEFuYWx5c2lzJw0Kb3V0cHV0Og0KICBodG1sX2RvY3VtZW50Og0KICAgIGNvZGVfZG93bmxvYWQ6IHllcw0KICAgIGZvbnRzaXplOiA4cHQNCiAgICBoaWdobGlnaHQ6IHRleHRtYXRlDQogICAgbnVtYmVyX3NlY3Rpb25zOiBubw0KICAgIHRoZW1lOiBmbGF0bHkNCiAgICB0b2M6IHllcw0KICAgIHRvY19mbG9hdDoNCiAgICAgIGNvbGxhcHNlZDogbm8NCi0tLQ0KDQpgYGB7ciBzZXR1cCwgaW5jbHVkZT1GQUxTRX0NCmtuaXRyOjpvcHRzX2NodW5rJHNldChjYWNoZSA9IFRSVUUpDQprbml0cjo6b3B0c19jaHVuayRzZXQoZWNobyA9IFRSVUUpDQprbml0cjo6b3B0c19jaHVuayRzZXQobWVzc2FnZSA9IEZBTFNFKQ0Ka25pdHI6Om9wdHNfY2h1bmskc2V0KHdhcm5pbmcgPSAgRkFMU0UpDQprbml0cjo6b3B0c19jaHVuayRzZXQoZmlnLndpZHRoPTMuMjUpDQprbml0cjo6b3B0c19jaHVuayRzZXQoZmlnLmhlaWdodD0yLjc1KQ0Ka25pdHI6Om9wdHNfY2h1bmskc2V0KGZpZy5hbGlnbj0nY2VudGVyJykgDQprbml0cjo6b3B0c19jaHVuayRzZXQocmVzdWx0cz0naG9sZCcpIA0KYGBgDQoNCmBgYHtyLCBlY2hvPUZBTFNFLCB3YXJuaW5nPUZBTFNFfQ0KbGlicmFyeShrbml0cikNCmxpYnJhcnkoa2FibGVFeHRyYSkNCmBgYA0KDQpccGFnZWJyZWFrDQoNCiMgQSBQcmlvcmkgUG93ZXINCi0gUG93ZXIgPSAxIC0gVHlwZSBJSSBlcnJvciAobWlzc2luZyBhbiBlZmZlY3Qgd2hlbiB0aGUgZWZmZWN0IGlzIHByZXNlbnQpLiBCYXNpY2FsbHksIHRoZSBwcm9iYWJpbGl0eSB0aGF0IG91ciB0ZXN0IHdpbGwgcmVqZWN0IGEgZmFsc2UgbnVsbCBoeXBvdGhlc2lzLg0KLSBDb2hlbiAoMTk2Mi8xOTg4KSBzYWlkIHdlIG5lZWQgdG8ga25vdyB0aGUgKiplZmZlY3Qgc2l6ZSoqICppbiB0aGUgcG9wdWxhdGlvbiogYW5kIHdlIG5lZWQgdG8gc2V0IGFuICoqYWxwaGEgbGV2ZWwqKiB0byBzZXQgYSBjcml0ZXJpYSBmb3Igc2lnbmlmaWNhbmNlIHRvIGVzdGltYXRlIHRoZSBzYW1wbGUgc2l6ZSBuZWVkZWQgdG8gYWNoaWV2ZSBhIHNwZWNpZmljIHBvd2VyIGxldmVsDQogICAgLSBFZmZlY3Qgc2l6ZSBjYW4gYmUgZGVmaW5lZCBhcyB0aGUgZGlzdGFuY2UgYmV0d2VlbiBvdXIgZXhwZXJpbWVudGFsIGFuZCBjb250cm9sIGRpc3RyaWJ1dGlvbnM6IENvaGVuJ3MgJGQgPSBcZnJhY3tNLVxtdX17XHNpZ21hfSQgW29yIHRoZSBwZXJjZW50YWdlIG9mIHZhcmlhbmNlIGV4cGxhaW5lZCwgJFxldGFeMiA9IFxmcmFje2ReMn17ZF4yKzR9JF0gDQoNCg0KDQohW10oTWl4ZWQvUG93ZXJQbG90LnBuZyl7IHdpZHRoPTUwJSB9DQpcDQoNCg0KLSBQb3dlciBpbmNyZWFzZXMgYXMgYSBmdW5jdGlvbiBvZiBzYW1wbGUgc2l6ZSBhbmQgZWZmZWN0IHNpemUgYW5kIGxvd2VyaW5nIHRoZSBhbHBoYSAoLjA1IHRvIC4xKQ0KLSBCZWxvdyBpcyBwb3dlciBmb3IgKmJldHdlZW4tc3ViamVjdCogdC10ZXN0IGFjcm9zcyBkaWZmZXJlbnQgc2FtcGxlIHNpemVzIGZvciBkaWZmZXJlbnQgZWZmZWN0IHNpemVzDQoNCmBgYHtyLCAsIGVjaG89RkFMU0UsIG91dC53aWR0aD0nLjQ5XFxsaW5ld2lkdGgnLCBmaWcud2lkdGg9Mi4yNSwgZmlnLmhlaWdodD0yLjUsZmlnLnNob3c9J2hvbGQnLGZpZy5hbGlnbj0nY2VudGVyJ30NCmxpYnJhcnkocHdyKQ0KbGlicmFyeShnZ3Bsb3QyKSANCnRoZW1lX3NldCh0aGVtZV9idygpKQ0KSW5kLkZpbmQuUG93ZXI8LWZ1bmN0aW9uKE4sZHNldCl7DQogICAgcHdyLnQudGVzdChuID0gTiwgZCA9IGRzZXQsIHNpZy5sZXZlbCA9IDAuMDUsIHBvd2VyID0gTlVMTCwgDQogICAgdHlwZSA9IGMoInR3by5zYW1wbGUiKSkkcG93ZXINCn0NCg0KTjwtc2VxKDUsMjAwLDEpDQpQb3dlclJhbmdlLmQuMjwtbWFwcGx5KEluZC5GaW5kLlBvd2VyLE4sLjIpDQpQb3dlclJhbmdlLmQuNDwtbWFwcGx5KEluZC5GaW5kLlBvd2VyLE4sLjQpDQpQb3dlclJhbmdlLmQuODwtbWFwcGx5KEluZC5GaW5kLlBvd2VyLE4sLjgpDQpxcGxvdChOLFBvd2VyUmFuZ2UuZC4yLCBnZW9tPWMoImxpbmUiKSwNCiAgICAgIG1haW49ImQgPSAuMiwgYSA9IC4wNSwgQlMiLCB4bGFiPSJTYW1wbGUgU2l6ZSBQZXIgR3JvdXAiLCB5bGFiPSJQb3dlciIsIHlsaW09YygwLDEpKSsNCiAgZ2VvbV9obGluZSh5aW50ZXJjZXB0PS44LCBjb2xvcj0ncmVkJykNCg0KcXBsb3QoTixQb3dlclJhbmdlLmQuNCwgZ2VvbT1jKCJsaW5lIiksDQogICAgICBtYWluPSJkID0gLjQsIGEgPSAuMDUsIEJTIiwgeGxhYj0iU2FtcGxlIFNpemUgUGVyIEdyb3VwIiwgeWxhYj0iUG93ZXIiLCB5bGltPWMoMCwxKSkrDQogIGdlb21faGxpbmUoeWludGVyY2VwdD0uOCwgY29sb3I9J3JlZCcpDQoNCnFwbG90KE4sUG93ZXJSYW5nZS5kLjgsIGdlb209YygibGluZSIpLA0KICAgICAgbWFpbj0iZCA9IC44LCBhID0gLjA1LCBCUyIsIHhsYWI9IlNhbXBsZSBTaXplIFBlciBHcm91cCIsIHlsYWI9IlBvd2VyIiwgeWxpbT1jKDAsMSkpKw0KICBnZW9tX2hsaW5lKHlpbnRlcmNlcHQ9LjgsIGNvbG9yPSdyZWQnKQ0KYGBgDQoNCi0gQmVsb3cgaXMgcG93ZXIgZm9yICp3aXRoaW4tc3ViamVjdCogdC10ZXN0IGFjcm9zcyBkaWZmZXJlbnQgc2FtcGxlIHNpemVzIGZvciBkaWZmZXJlbnQgZWZmZWN0IHNpemVzDQoNCmBgYHtyLCBlY2hvPUZBTFNFLG91dC53aWR0aD0nLjQ5XFxsaW5ld2lkdGgnLCBmaWcud2lkdGg9Mi4yNSwgZmlnLmhlaWdodD0yLjUwLGZpZy5zaG93PSdob2xkJyxmaWcuYWxpZ249J2NlbnRlcid9DQpQYWlyZWQuRmluZC5Qb3dlcjwtZnVuY3Rpb24oTixkc2V0KXsNCiAgICBwd3IudC50ZXN0KG4gPSBOLCBkID0gZHNldCwgc2lnLmxldmVsID0gMC4wNSwgcG93ZXIgPSBOVUxMLCANCiAgICB0eXBlID0gYygicGFpcmVkIikpJHBvd2VyDQp9DQoNCk48LXNlcSg1LDIwMCwxKQ0KUG93ZXJSYW5nZS5kLjIucDwtbWFwcGx5KFBhaXJlZC5GaW5kLlBvd2VyLE4sLjIpDQpQb3dlclJhbmdlLmQuNC5wPC1tYXBwbHkoUGFpcmVkLkZpbmQuUG93ZXIsTiwuNCkNClBvd2VyUmFuZ2UuZC44LnA8LW1hcHBseShQYWlyZWQuRmluZC5Qb3dlcixOLC44KQ0KcXBsb3QoTixQb3dlclJhbmdlLmQuMi5wLCBnZW9tPWMoImxpbmUiKSwNCiAgICAgIG1haW49ImQgPSAuMiwgYSA9IC4wNSwgV1MiLCB4bGFiPSJTYW1wbGUgU2l6ZSIsIHlsYWI9IlBvd2VyIiwgeWxpbT1jKDAsMSkpKw0KICBnZW9tX2hsaW5lKHlpbnRlcmNlcHQ9LjgsIGNvbG9yPSdyZWQnKQ0KcXBsb3QoTixQb3dlclJhbmdlLmQuNC5wLCBnZW9tPWMoImxpbmUiKSwNCiAgICAgIG1haW49ImQgPSAuNCwgYSA9IC4wNSwgV1MiLCB4bGFiPSJTYW1wbGUgU2l6ZSIsIHlsYWI9IlBvd2VyIix5bGltPWMoMCwxKSkrDQogIGdlb21faGxpbmUoeWludGVyY2VwdD0uOCwgY29sb3I9J3JlZCcpDQpxcGxvdChOLFBvd2VyUmFuZ2UuZC44LnAsIGdlb209YygibGluZSIpLA0KICAgICAgbWFpbj0iZCA9IC44LCBhID0gLjA1LCBXUyIsIHhsYWI9IlNhbXBsZSBTaXplIiwgeWxhYj0iUG93ZXIiLCB5bGltPWMoMCwxKSkrDQogIGdlb21faGxpbmUoeWludGVyY2VwdD0uOCwgY29sb3I9J3JlZCcpDQpgYGANCg0KLSBCZWxvdyBpcyB3ZSBzb2x2ZSBmb3IgdGhlIHNhbXBsZSBzaXplIG5lZWRlZCBpZiB3ZSB3YW50IHRvIGFjaGlldmUgYW4gYSBwcmlvcmkgIHBvd2VyIG9mIC44MCBmb3IgYSAqd2l0aGluLXN1YmplY3QqICYgKmJldHdlZW4tc3ViamVjdCogdC10ZXN0IGFjcm9zcyBkaWZmZXJlbnQgZWZmZWN0IHNpemVzDQoNCmBgYHtyLCBlY2hvPUZBTFNFLCBvdXQud2lkdGg9Jy40OVxcbGluZXdpZHRoJywgZmlnLndpZHRoPTMuMDAsIGZpZy5oZWlnaHQ9Mi41LGZpZy5zaG93PSdob2xkJyxmaWcuYWxpZ249J2NlbnRlcid9DQpJbmQuRmluZC5OPC1mdW5jdGlvbihkc2V0KXsNCiAgICBwd3IudC50ZXN0KG4gPSBOVUxMLCBkID0gZHNldCwgc2lnLmxldmVsID0gMC4wNSwgcG93ZXIgPSAuOCwgDQogICAgdHlwZSA9IGMoInR3by5zYW1wbGUiKSkkbioyDQp9DQoNClBhaXJlZC5GaW5kLk48LWZ1bmN0aW9uKGRzZXQpew0KICAgIHB3ci50LnRlc3QobiA9IE5VTEwsIGQgPSBkc2V0LCBzaWcubGV2ZWwgPSAwLjA1LCBwb3dlciA9IC44LCANCiAgICB0eXBlID0gYygicGFpcmVkIikpJG4NCn0NCg0KZHJhbmdlPC1zZXEoLjIsMSwuMDEpDQpTYW1wbGVOZWVkZWQ8LXNhcHBseShkcmFuZ2UsSW5kLkZpbmQuTikNClNhbXBsZU5lZWRlZFBhaXJlZDwtc2FwcGx5KGRyYW5nZSxQYWlyZWQuRmluZC5OKQ0KDQpxcGxvdChkcmFuZ2UsU2FtcGxlTmVlZGVkLCBnZW9tPWMoImxpbmUiKSwNCiAgICAgIG1haW49IlBvd2VyID0gLjgsIGEgPSAuMDUsIEJTIiwgeGxhYj0iQ29oZW4ncyBkIiwgeWxhYj0iVG90YWwgU2FtcGxlIFNpemUgTmVlZGVkIikNCnFwbG90KGRyYW5nZSxTYW1wbGVOZWVkZWRQYWlyZWQsIGdlb209YygibGluZSIpLA0KICAgICAgbWFpbj0iUG93ZXIgPSAuOCwgYSA9IC4wNSwgV1MiLCB4bGFiPSJDb2hlbidzIGQiLCB5bGFiPSJUb3RhbCBTYW1wbGUgU2l6ZSBOZWVkZWQiKQ0KDQpgYGANCg0KDQojIyBBIFByaW9yaSBQb3dlciBQcm9ibGVtcw0KLSBJcyBpdCBwb3NzaWJsZSB0byBrbm93IHRoZSBwb3B1bGF0aW9uIGVmZmVjdCBzaXplPw0KICAgIC0gTWlnaHQgaXQgYWxsIHJlYWxseSBkZXBlbmQgb24gY29udGV4dHVhbCBmYWN0b3JzICh3aGVyZSB5b3UgY29sbGVjdCB5b3VyIGRhdGEsIHdobyBjb2xsZWN0ZWQgZGF0YSwgaG93IHF1ZXN0aW9ucyBhcmUgYXNrZWQsIGV0Yy4pPw0KICAgIC0gSW4gb3RoZXIgd29yZHMsIHBvcHVsYXRpb24gZWZmZWN0IHNpemUgd2lsbCB2YXJ5IGFzIGEgZnVuY3Rpb24gb2YgaG93IHRvIGNvbmR1Y3QgeW91ciBzdHVkeQ0KLSBPZnRlbiB3ZSBlc3RpbWF0ZWQgYSBwcmlvcmkgcG93ZXIgdHdvIHdheXMNCiAgICAtIEEpIEd1ZXNzIHRoYXQgd2FzIG1lZGl1bSBvciBzbWFsbA0KICAgIC0gQikgR3Vlc3MgaXQgZnJvbSBwcmlvciBwYXBlcnMgb3IgcGlsb3Qgc3R1ZGllcyAoT2JzZXJ2ZWQgZWZmZWN0IHNpemVzKQ0KICAgICAgICAtIFBpbG90IHN0dWRpZXMgYXJlIGRlc2lnbmVkIHRvIGJlICoqdW5kZXItcG93ZXJlZCoqICANCg0KIyBPYnNlcnZlZCBQb3dlci9FZmZlY3QgU2l6ZXMNCi0gVGhpcyBpcyB0aGUgcHJvY2VzcyBvZiB0YWtpbmcgc29tZW9uZSBlbHNlIHN0dWR5IChvciBhIHNtYWxsIHNhbXBsZSBwaWxvdCBzdHVkeSB5b3UgY29uZHVjdCksIHVzaW5nIHRoZSBlZmZlY3Qgc2l6ZSB0aGF0IGlzIGZvdW5kIHVzaW5nIGl0IGZvciB5b3VyIHBvd2VyIGFuYWx5c2lzDQogICAgLSBBKSBVc2luZyBwdWJsaXNoZWQgbGl0ZXJhdHVyZSBoYXMgdGhlIHByb2JsZW0gb2Ygb25seSBwdWJsaXNoaW5nIHNpZ25pZmljYW50IGVmZmVjdHMgKHdoaWNoIGluZmxhdGVzIHRoZSBlZmZlY3Qgc2l6ZSBlc3RpbWF0ZSBvZiB0aGUgcG9wdWxhdGlvbikNCiAgICAtIEIpIFVzaW5nIHBpbG90IHN0dWRpZXMgd2l0aCBzbWFsbCBzYW1wbGVzIGNhbiBpbmZsYXRlIHRoZSBlZmZlY3Qgc2l6ZXMgYmVjYXVzZSBpbiBzbWFsbCBzYW1wbGVzIHlvdSBnZXQgYSBkZWZsYXRlZCBlc3RpbWF0ZSBvZiB0aGUgc3RhbmRhcmQgZGV2aWF0aW9uLCB3aGljaCBpbmZsYXRlcyB5b3VyIGVmZmVjdCBzaXplIChzZWUgQW5kZXJzb24sIEtlbGxleSwgJiBNYXh3ZWxsLCAyMDE3IGZvciByZXZpZXcgb24gYm90aCB0aGVzZSBpc3N1ZXMpDQoNCiMjIE9ic2VydmVkIFBvd2VyIEZvcm11bGFzDQotIFlvdSBnbyB0byBhbiBvbGQgcHVibGlzaGVkIHBhcGVyIG9uIHRoZSBieXN0YW5kZXIgZWZmZWN0IChDYW1wYmVsbCwgMTk3NCkgYW5kIHlvdSBmaW5kIHRoZXkgaGF2ZSBhbiBlZmZlY3Qgc2l6ZSBvZiBoZWRnZSdzIGcgPSAxLjc5OCAod2hpY2ggaXMgYSBjb3JyZWN0ZWQgQ29oZW4ncyBkKSB3aXRoIG4gPSAxMiBwZXIgZ3JvdXAgKGJldHdlZW4tc3ViamVjdCB0LXRlc3Qgd2l0aCBhbiBhID0gLjA1KQ0KDQpgYGB7cn0NCk9iUG93ZXI8LXB3ci50LnRlc3QobiA9IDEyLCBkID0gMS43OTgsIHNpZy5sZXZlbCA9IDAuMDUsIA0KICAgICAgICAgICBwb3dlciA9IE5VTEwsIHR5cGUgPSBjKCJ0d28uc2FtcGxlIikpJHBvd2VyDQpgYGANCg0KLSBUaGUgcG93ZXIgeW91IHdvdWxkIGVzdGltYXRlIGZyb20gdGhlaXIgc3R1ZHkgZ2l2ZW4gdGhlc2UgcGFyYW1ldGVycyB3b3VsZCBiZSAqb2JzZXJ2ZWQgcG93ZXIqID0gIGByIHJvdW5kKE9iUG93ZXIsMylgLiBUaGlzIGlzICphZnRlciB0aGUgZmFjdCogKCoqcG9zdC1ob2MqKikuICBJdCBpcyB0ZXJyaWJsZSBlc3RpbWF0ZSBvZiB3aGF0IHRoZWlyICphIHByaW9yaSogcG93ZXIgd2FzIChIb2VuaWcgJiBIZWlzZXksIDIwMDEpLiBJdCB0dXJucyBvdXQgdGhlIGJ5c3RhbmRlciBlZmZlY3QgaGFzIGFuIGVmZmVjdCBzaXplIG9mICpnKiA9IC4zNSAoTWV0YS1BbmFseXNpczsgRmlzY2hlciBldCBhbCwgMjAxMSkuIEdpdmVuIHRoaXMgdmFsdWUgd2hhdCB3YXMgdGhlaXIgYSBwcmlvcmkgcG93ZXI/IA0KDQpgYGB7cn0NCmFwcmlvcmlQb3dlcjwtcHdyLnQudGVzdChuID0gMTIsIGQgPSAuMzUsIHNpZy5sZXZlbCA9IDAuMDUsIA0KICAgICAgICAgICBwb3dlciA9IE5VTEwsIHR5cGUgPSBjKCJ0d28uc2FtcGxlIikpJHBvd2VyDQpgYGANCg0KLSBHaXZlbiBOID0gMTIgcGVyIGdyb3VwIHRoZXkgd291bGQgaGF2ZSBhbiAqYSBwcmlvcmkgcG93ZXIqID0gIGByIHJvdW5kKGFwcmlvcmlQb3dlciwzKWAuDQotIEhvdyBkaWQgdGhleSBnZXQgc3VjaCBhIGxhcmdlIG51bWJlcj8gDQoNCiMjIE9ic2VydmVkIFBvd2VyIFNpbXVsYXRpb25zDQotIFVzaW5nIE1vbnRlLUNhcmxvIHNpbXVsYXRpb24gbWV0aG9kcywgaGVyZSBhcmUgc2ltdWxhdGlvbnMgcmVzdWx0cyBvZiB3aGF0IGhhcHBlbnMgdG8geW91ciBlZmZlY3Qgc2l6ZXMgaWYgeW91IHVzZSBlaXRoZXIgcGlsb3QgKHVuZGVyLXBvd2VyZWQgc3R1ZGllczogc2F5IFBvd2VyIG9mIC4xMikgb3IgZnJvbSBwdWJsaXNoZWQgbGl0ZXJhdHVyZSAod2hpY2ggb2Z0ZW4gcHVibGlzaGVzIGluZmxhdGVkIHJlc3VsdHMsIHNlZSBJb2FubmlkaXMsIDIwMDUpDQotIFRoZSBsaW5lIHJlcHJlc2VudGVkIHRoZSAqbWVkaWFuIG9ic2VydmVkIGVmZmVjdCBzaXplIC0gcG9wIGVmZmVjdCBzaXplIC8gcG9wIGVmZmVjdCBzaXplKiBbMUsgc2ltdWxhdGlvbnNdDQoNCiFbSW5mbGF0aW9uIFJhdGVdKE1peGVkL0luZmxhdGVSYXRlLnBuZyl7IHdpZHRoPTQ1JSB9DQpcDQoNCi0gVGhpcyByZXN1bHRzIGluIHRoZSBwcm9ibGVtIHRoYXQgeW91IGFyZSBlc3RpbWF0aW5nIHRoZSBzYW1wbGUgc2l6ZSB0b28gc21hbGwgZm9yIHlvdXIgcG9wdWxhdGlvbiBlZmZlY3Qgc2l6ZSBhbmQgdGh1cyB5b3VyIHJlcGxpY2FiaWxpdHkgcmF0ZSBpcyBsb3dlcmVkDQoNCg0KIVtSZXBsaWNhYmlsaXR5IHJhdGVdKE1peGVkL1IuUGxvdC5HLnBuZyl7IHdpZHRoPTQwJSB9DQpcDQoNCi0gU28gcGlsb3Qgc3R1ZGllcyBkb24ndCBsb29rIHRoYXQgYmFkLCByaWdodD8gWW91IHNlZSB0aGUgbWVkaWFuIG9mIDEwMDAgc2ltdWxhdGlvbnMuIFRoZSBwcm9ibGVtIGlzIGxvb2sgYXQgdGhlIHJhbmdlIG9mIHBvc3NpYmxlIGVmZmVjdCBzaXplcy4gDQoNCmBgYHtyLCBlY2hvPUZBTFNFfQ0KRHNpbTwtZnVuY3Rpb24oUGFyYW1zKSB7DQogIFRydWVEPC1QYXJhbXNbWzFdXTsgYWxwaGE8LVBhcmFtc1tbMl1dDQogIE4xPC1QYXJhbXNbWzNdXTsgTjI8LVBhcmFtc1tbNF1dDQogICMgU2V0IGRpc3Ryb2J1dGlvbnMNCiAgQ29udHJvbDwtcm5vcm0oTjEsIG1lYW4gPSAwLCBzZCA9IDEpDQogIEV4cDwtcm5vcm0oTjIsIG1lYW4gPSBUcnVlRCwgc2QgPSAxKQ0KICAjIFJ1biB0LWVzdA0KIE9ic2VydmVkLmQ8LWFicygobWVhbihFeHApLW1lYW4oQ29udHJvbCkpL3NkKENvbnRyb2wpKQ0KICByZXR1cm4oT2JzZXJ2ZWQuZCkNCn0NCiMgUGFyYW1hdGVycw0KZCA9IC4zNTsgYWxwaGE9IC4wNTsgTjE9MTI7IE4yPTEyOyBTaW09MTAwMDANCiMgUnVuIHNpbXVsYXRpb24NCk9ic2VydmVkLmQ8LXJlcGxpY2F0ZShTaW0sRHNpbShjKGQsYWxwaGEsTjEsTjIpKSkNCnFwbG90KE9ic2VydmVkLmQsIGdlb20gPSAnZGVuc2l0eScsIGZpbGw9IEkoImJsdWUiKSwNCiAgICAgIG1haW49IlJhbmdlIG9mIE9ic2VydmVkIGQiLCB4bGFiPSJPYnNlcnZlZCBDb2hlbidzIGQiLCB5bGFiPSJEZW5zaXR5IikNCmBgYA0KVGhlcmUgaXMgYSBsb25nIHRhaWwgdGhlcmUgd2hpY2ggc2F5IHlvdSBjYW4gZWFzaWx5IHRoaW5rIHlvdSBoYXZlIGEgYmlnIGVmZmVjdC4NCg0KYGBge3IsIGVjaG89RkFMU0V9DQpsaWJyYXJ5KGNhVG9vbHMpDQpEY29udmVydCA8LSBkZW5zaXR5KE9ic2VydmVkLmQsIGtlcm5lbD0nY29zaW5lJykgIyByZXR1cm5zIHRoZSBkZW5zaXR5IGRhdGEgDQphYm92ZUc8LXJvdW5kKHRyYXB6KERjb252ZXJ0JHhbRGNvbnZlcnQkeCA+PSAuMzVdLERjb252ZXJ0JHlbRGNvbnZlcnQkeCA+PSAuMzVdKSoxMDAsMykNCmFib3ZlTDwtcm91bmQodHJhcHooRGNvbnZlcnQkeFtEY29udmVydCR4ID49IC44XSxEY29udmVydCR5W0Rjb252ZXJ0JHggPj0gLjhdKSoxMDAsMykNCmFib3ZlT2JkPC1yb3VuZCh0cmFweihEY29udmVydCR4W0Rjb252ZXJ0JHggPj0gMS43OThdLERjb252ZXJ0JHlbRGNvbnZlcnQkeCA+PSAxLjc5OF0pKjEwMCwzKQ0KYGBgDQoNCi0gR2l2ZW4gTiA9IDEyIHBlciBncm91cCBhbmQgYXNzdW1pbmcgbm8gaGFja2luZw0KICAgIC0gdGhleSB3b3VsZCBoYWQgYWJvdXQgYHIgYWJvdmVHYCUgdG8gZmluZCBhICpkKiA+PSAuMzUgKFBvcHVsYXRpb24pLg0KICAgIC0gdGhleSB3b3VsZCBoYWQgYWJvdXQgYHIgYWJvdmVMYCUgdG8gZmluZCBhICpkKiA+PSAuOCAoTGFyZ2UpLg0KICAgIC0gdGhleSB3b3VsZCBoYWQgYWJvdXQgYHIgYWJvdmVPYmRgJSB0byBmaW5kIGEgKmQqID49IDEuNzk4IChPYnNlcnZlZCkuDQoNCi0gSG93ZXZlciwgYXMgeW91IHNhdyB3aXRoIHRoZSByZXBsaWNhYmlsaXR5IHJhdGUsIHlvdSBhcmUgZmFyIGJldHRlciBwaWxvdGluZyB0aGFuIGFzc3VtaW5nIGFuIGVmZmVjdCBzaXplIGZyb20gcHVibGlzaGVkIHBhcGVycyAodW5sZXNzIGl0J3MgYSBtZXRhLWFuYWx5c2lzKS4gDQoNCi0gVGFrZSBhd2F5IG1lc3NhZ2UgaXMgaXQgaXMgaGFyZCB0byBrbm93IHdoYXQgaXMgcmVhbCBhbmQgd2hhdCBpcyBub3QgKHJlcGVhdGVkIHJlcGxpY2F0aW9ucyBhcmUgbmVlZGVkIG9yIG1ldGEtYW5hbHlzaXMpDQotIEluIHByYWN0aWNlIHdoYXQgdG8gZG8/DQogICAgLSBGb3JtdWxhLWJhc2VkIGFwcHJvYWNoIHVzaW5nIGVzdGltYXRlZCBlZmZlY3Qgc2l6ZSAoa2VlcGluZyBpbiBtaW5kIHB1YmxpY2F0aW9uIGJpYXMpDQogICAgLSBTaW11bGF0aW9uLWJhc2VkIGFwcHJvYWNoZXMgDQogICAgDQojIEZvcm11bGEtYmFzZWQgYXBwcm9hY2ggDQotICBTaGlueSBBcHA6IFdlc3RmYWxsLCBKdWRkICYgS2VubnksIDIwMTQgJiBKdWRkLCBXZXN0ZmFsbCAmIEtlbm55LCAyMDE3IA0KDQoxKSBFc3RpbWF0aW5nIGEgQ29oZW4ncyBkIA0KJCRkID0gXGZyYWN7TV9kfXtcc3FydChcc2lnbWFfe0ludGVyY2VwdF97U3Vian19XjIrXHNpZ21hX3tJbnRlcmNlcHRfe2l0ZW19fV4yK1xzaWdtYV97U2xvcGVfe1N1Ymp9fV4yK1xzaWdtYV97U2xvcGVfe0l0ZW19fV4yK1xzaWdtYV97UmVzaWR9XjIpfSAgICQkDQoNCjIpIENvbnZlcnRpbmcgeW91ciB2YXJpYW5jZSBjb21wb25lbnRzIGludG8gVmFyaWFuY2UgUGFydGl0aW9uaW5nIENvZWZmaWNpZW50cyAoVlBDKSwgd2hpY2gganVzdCB0aGUgcmVsYXRpdmUgdGhlIHBlcmNlbnRhZ2Ugb2YgY29tcG9uZW50IChWYXJpYW5jZSBUZXJtLyBTdW0gUmFuZG9tIFZhcmlhbmNlKSANCg0KMykgVXNlIGhpcyBzaGlueSBhcHAgKG9yIGRvd25sb2FkIGhpcyBjb2RlIGFuZCBleHRyYWN0IHRoZSBmdW5jdGlvbnMpDQotIE9uZSBDcm9zc2VkIEZhY3RvcjogaHR0cHM6Ly9qYWtld2VzdGZhbGwuc2hpbnlhcHBzLmlvL2Nyb3NzZWRwb3dlci8gDQotIFR3byBDcm9zc2VkL05lc3RlZCBGYWN0b3JzOiBodHRwczovL2pha2V3ZXN0ZmFsbC5zaGlueWFwcHMuaW8vdHdvX2ZhY3Rvcl9wb3dlci8NCg0KDQojIyBFeGFtcGxlDQpXZSB3aWxsIHVzZSB0aGUgc2ltdWxhdGVkIGRhdGEgZnJvbSBsYXN0IHdlZWsgKGEgZnVsbCBjcm9zc2VkIHN0dWR5IHdpdGggMzAgc3ViamVjdHMgYW5kIDEwIGl0ZW1zKSwgYnV0IGxvb2sgYXQgb25seSBvbmUgb2YgdGhlIGZhY3RvcnMgb24gYSBtYXhpbWFsIG1vZGVsLiANCi0gV2Ugd2lsbCB1c2UgdGhlIHNpbXVsYXRlZCBkYXRhIGZyb20gbGFzdCB3ZWVrDQo6IFNpbXBsaWZpZWQgbW9kZWwgZm9yIG5vdzogYCgxK0MxfHxTdWJqZWN0KSArICgxK0MxfHxJdGVtKWANCi0gQ29uZGl0aW9ucyB3ZXJlIGVmZmVjdHMgY29kZWQgJCgtLjUsIC41KSQNCi0gW0Rvd25sb2FkIERhdGFdKC9NaXhlZC9TaW04LmNzdikNCg0KYGBge3IsIGVjaD1GQUxTRX0NCkRhdGFTaW04PC1yZWFkLmNzdigiTWl4ZWQvU2ltOC5jc3YiKQ0KRGF0YVNpbTgkQzE8LWZhY3RvcihEYXRhU2ltOCRDb25kaXRpb24xKQ0KRGF0YVNpbTgkQzI8LWFzLmZhY3RvcihEYXRhU2ltOCRDb25kaXRpb24yKQ0KRGF0YVNpbTgkSXRlbTwtYXMuZmFjdG9yKERhdGFTaW04JEl0ZW0pDQpEYXRhU2ltOCRTdWJqZWN0PC1hcy5mYWN0b3IoRGF0YVNpbTgkU3ViamVjdCkNCmBgYA0KDQotIEZpeCB0aGUgbWF4aW1hbCBtb2RlbCAoYnV0IEkgd2lsbCBibG9jayB0aGUgY29ycmVsYXRpb25zKSBmb3IgYSBmdWxsIGNyb3NzZWQgZGVzaWduIFthZ2FpbiB3ZSB3aWxsIGp1c3QgaWdub3JlIENvbmRpdGlvbiAyIGZvciBub3ddDQoNCmBgYHtyfQ0KbGlicmFyeShsbWU0KQ0KTWF4TW9kZWw8LWxtZXIoRFZfU1NfUlNsb3BlX1NTTm9pc2VfSXRlbXMgfiBDb25kaXRpb24xDQogICAgICAgICAgICAgICsoMStDb25kaXRpb24xfHxTdWJqZWN0KQ0KICAgICAgICAgICAgICArKDErQ29uZGl0aW9uMXx8SXRlbSksDQogICAgICAgICAgICAgIGRhdGE9RGF0YVNpbTgsIFJFTUw9RkFMU0UpDQpzdW1tYXJ5KE1heE1vZGVsLCBjb3JyZWxhdGlvbj1GQUxTRSkNCmBgYA0KDQotIFdlIHdpbGwgdXNlIHRoZSBicm9vbSBwYWNrYWdlIHRvIGV4dHJhY3QgdGhlIHJhbmRvbSBlZmZlY3RzIHdlIG5lZWQNCg0KYGBge3J9DQpsaWJyYXJ5KGJyb29tKQ0KUmFuZG9tRWZmZWN0PC10aWR5KE1heE1vZGVsLCBlZmZlY3RzID0gYygicmFuX3BhcnMiKSwgc2NhbGU9InZjb3YiKQ0KYGBgDQoNCmBgYHtyLCBlY2hvPUZBTFNFfQ0Ka2FibGUoUmFuZG9tRWZmZWN0KSAlPiUNCiAga2FibGVfc3R5bGluZyhib290c3RyYXBfb3B0aW9ucyA9IGMoInN0cmlwZWQiLCAiaG92ZXIiLCAiY29uZGVuc2VkIiwgInJlc3BvbnNpdmUiLCBmdWxsX3dpZHRoID0gRikpDQpgYGANCg0KIyMjIEdlbmVyYXRlIHRoZSBlc3RpbWF0ZWQgKmQqDQoNCmBgYHtyfQ0KTWQ8LXN1bW1hcnkoTWF4TW9kZWwpJGNvZWZbMl0NClNEUGFydDwtc3FydChzdW0oUmFuZG9tRWZmZWN0JGVzdGltYXRlKSkNCmQubWl4ZWQgPSBNZCAvIFNEUGFydA0KYGBgDQoNCi0gV2UgZ2V0IGEgKmQqID0gYHIgcm91bmQoZC5taXhlZCwzKWANCg0KIyMjIEdlbmVyYXRlIHRoZSBWUEMNCmBgYHtyfQ0KUmFuZG9tRWZmZWN0JFZQQzwtUmFuZG9tRWZmZWN0JGVzdGltYXRlL3N1bShSYW5kb21FZmZlY3QkZXN0aW1hdGUpDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQprYWJsZShSYW5kb21FZmZlY3QpICU+JQ0KICBrYWJsZV9zdHlsaW5nKGJvb3RzdHJhcF9vcHRpb25zID0gYygic3RyaXBlZCIsICJob3ZlciIsICJjb25kZW5zZWQiLCAicmVzcG9uc2l2ZSIpKQ0KYGBgDQoNCi0gVXNpbmcgdGhlIHdlYnNpdGUsIGh0dHBzOi8vamFrZXdlc3RmYWxsLnNoaW55YXBwcy5pby9jcm9zc2VkcG93ZXIvIA0KICAgIC0gd2UgZmluZCBhIHBvd2VyIG9mIC43ODggYmFzZWQgb24gdGhlc2UgcGFyYW1ldGVycw0KICAgIC0gYXNzdW1pbmcgb3VyICpkKiBpcyBjb3JyZWN0LCB0aGUgd2Vic2l0ZSBsZXRzIHVzIHNvbHZlIGZvciBzYW1wbGUgc2l6ZSwgc28gYXQgcG93ZXIgLjgwLCBpdCBzYXlzIHdlIG5lZWQgMzYgc3ViamVjdHMgYW5kIDEwIGl0ZW1zICANCg0KIyMgTGltaXRhdGlvbnMNCi0gT25seSB3b3JrcyBmb3Igc3R1ZGllcyB3aGVyZSBmYWN0b3JzIGhhdmUgMiBsZXZlbHMsIGFuZCB3ZSBtZWV0IGFsbCB0aGUgb3RoZXIgYXNzdW1wdGlvbnMgKHNlZSBCcnlzYmFlcnQgJiBTdGV2ZW5zLCAyMDE4KQ0KLSBXZSBhcmUgbm90IHN1cmUgaG93IHRoaXMgbWV0aG9kIHdvcmtzIHdoZW4geW91IGZvbGxvdyBwYXJzaW1vbmlvdXMgbW9kZWxpbmcgKGFzIHdlIGRpZCBsYXN0IHdlZWspLiBXZSBzYXcgbGFzdCAyIHdlZWtzIHRoYXQgb3ZlciBzcGVjaWZpZWQgbW9kZWxzIHByb2R1Y2UgdW5pbnRlcnByZXRhYmxlIHJhbmRvbSBlZmZlY3RzIGFuZCBhbHNvIGRlZmxhdGUgcG93ZXINCg0KIyBTaW11bGF0aW9uLWJhc2VkIGFwcHJvYWNoDQotIFIgYWxsb3dzIGZvciB0aGUgTW9udGUtQ2FybG8gbWV0aG9kLCByZXBlYXRlZCBzaW11bGF0aW9ucyBiYXNlZCBvbiBhc3N1bXB0aW9ucyB0byBmaW5kIHNvbHV0aW9ucw0KLSBIZXJlIGlzIGEgTW9udGUtQ2FybG8gc29sdXRpb24gdG8gdC10ZXN0IHBvd2VyLCB3aGVyZSBJIGFzc3VtZSBlYWNoIGdyb3VwIGZvbGxvd3MgYSBub3JtYWwgZGlzdHJpYnV0aW9uDQoNCmBgYHtyfQ0KTUMudHRlc3QgPC1mdW5jdGlvbihQYXJhbXMpIHsNCiAgVHJ1ZUQ8LVBhcmFtc1tbMV1dOyBhbHBoYTwtUGFyYW1zW1syXV0NCiAgTjE8LVBhcmFtc1tbM11dOyBOMjwtUGFyYW1zW1s0XV0NCiAgIyBTZXQgZGlzdHJvYnV0aW9ucw0KICBDb250cm9sPC1ybm9ybShOMSwgbWVhbiA9IDAsIHNkID0gMSkNCiAgRXhwPC1ybm9ybShOMiwgbWVhbiA9IFRydWVELCBzZCA9IDEpDQogICMgUnVuIHQtZXN0DQogIGNhbGNQPC10LnRlc3QoRXhwLENvbnRyb2wsDQogICAgICAgICAgICAgICAgYWx0ZXJuYXRpdmUgPSBjKCJ0d28uc2lkZWQiKSwNCiAgICAgICAgICAgICAgICBwYWlyZWQgPSBGQUxTRSwgdmFyLmVxdWFsID0gVFJVRSwNCiAgICAgICAgICAgICAgICBjb25mLmxldmVsID0gMS1hbHBoYSkkcC52YWx1ZQ0KICAgcmVzdWx0PC1jYWxjUA0KICByZXR1cm4ocmVzdWx0KQ0KfQ0KIyBQYXJhbWF0ZXJzDQpkID0gLjg7IGFscGhhPSAuMDU7IE4xPTIwOyBOMj0yMDsgU2ltPTEwMDANCiMgUnVuIHNpbXVsYXRpb24NClB2YWx1ZXM8LXJlcGxpY2F0ZShTaW0sTUMudHRlc3QoYyhkLGFscGhhLE4xLE4yKSkpDQpTaWc8LWlmZWxzZShQdmFsdWVzIDw9IGFscGhhLCAxLCAwKQ0KUG93ZXJNQzwtc3VtKFNpZykvU2ltICAgICAgICAgICAgDQpgYGANCg0KYGBge3IsIGVjaG89RkFMU0V9DQpQb3dlckZvcm08LXB3ci50LnRlc3QobiA9IE4xLCBkID0gZCwgc2lnLmxldmVsID0gMC4wNSwgDQogICAgICAgICAgIHBvd2VyID0gTlVMTCwgdHlwZSA9IGMoInR3by5zYW1wbGUiKSkkcG93ZXINCmBgYA0KDQpTaW11bGF0ZWQgUG93ZXIgPSBgciBQb3dlck1DYCB3aGljaCBzaG91bGQgYmUgdmVyeSBjbG9zZSB0byBhIGZvcm11bGEgc29sdXRpb24gYHIgUG93ZXJGb3JtYCANCg0KLSBXZSB3b3VsZCBoYXZlIHRvIGJ1aWxkIHNpbXVsYXRpb25zIGxpa2UgdGhpcyBmb3IgZWFjaCBhbmQgZXZlcnkgZGVzaWduIHdlIHdhbnRlZCB0byB0ZXN0IGFuZCBmb3IgbWl4ZWQgbW9kZWxzLCB0aGlzIGlzIGEgbG90IG9mIHByb2dyYW1taW5nISANCiANCiMgU2ltciBwYWNrYWdlDQotIFNpbXIgcGFja2FnZSBtYWtlcyBpdCBlYXNpZXIgdG8gZG8gdGhpcyBraW5kIG9mIHNpbXVsYXRpb25zIA0KICAgIC0gVGhlIHBhY2thZ2UgaXMgbm90IHdlbGwgZG9jdW1lbnRlZCBhbmQgaXRzIHNvcnQgb2YgYnVnZ3kgKGJ1dCBzbyBmYXIgaXRzIGVhc2llc3QgdG8gdXNlKQ0KLSBZb3UgY2FuIHVzZSBpdCBjb25zdHJ1Y3QgYSBzaW11bGF0aW9uIGJhc2VkIG9uIHBhcmFtZXRlcnMgKGxpa2UgV2VzdGZhbGwgZXQgYWwuKSwgYnV0IGl0IHNpbXVsYXRlcyB0aGUgcG93ZXIgb3IgeW91IGNhbiBiYXNlIGl0IG9uIGEgcHJldmlvdXMgbW9kZWwNCg0KIyMgU2ltdWxhdGlvbiBmcm9tIFBhcmFtZXRlcnMNCi0gTGV0J3MgcmVkbyBvdXIgZXhwZXJpbWVudCBmcm9tIGFib3ZlDQotIFRoaXMgaXMgYmFzaWNhbGx5IGdvaW5nIHRvIGdpdmUgYW4gKm9ic2VydmVkIHBvd2VyKg0KLSBTdGFydCBieSBzcGVjaWZ5aW5nIHRoZSBudW1iZXIgb2Ygc3ViamVjdHMgKCpuKiA9IDMwKSBhbmQgaXRlbXMgKCpuKiA9IDEwKQ0KDQpgYGB7cn0NCmxpYnJhcnkoc2ltcikNCkl0ZW0gPC0gYXMuZmFjdG9yKHJlcCgxOjEwKSkNClN1YmplY3QgPC0gYXMuZmFjdG9yKHJlcCgxOjMwKSkNCkNvbmRpdGlvbjE8LXJlcCgtLjU6LjUpDQojIGNyZWF0ZXMgImZyYW1lIiBmb3Igb3VyIGRhdGENClggPC0gZXhwYW5kLmdyaWQoU3ViamVjdD1TdWJqZWN0LEl0ZW09SXRlbSwgQ29uZGl0aW9uMT1Db25kaXRpb24xKQ0KYGBgDQoNCmBgYHtyLCBlY2hvPUZBTFNFfQ0Ka2FibGUoaGVhZChYKSkgJT4lDQogIGthYmxlX3N0eWxpbmcoYm9vdHN0cmFwX29wdGlvbnMgPSBjKCJzdHJpcGVkIiwgImhvdmVyIiwgImNvbmRlbnNlZCIsICJyZXNwb25zaXZlIikpDQpgYGANCg0KDQotIE5leHQsIHdlIG5lZWQgdG8gc3BlY2lmeSAod2Ugd2lsbCBzZXQgdGhlIHJhbmRvbSBjb3JyZWxhdGlvbiB0byBiZSB6ZXJvIGZvciBub3cpDQogICAgLSBGaXhlZCB0ZXJtcw0KICAgICAgICAtIEludGVyY2VwdCAmIENvbmRpdGlvbiAgW2ludGVyY2VwdCA9IDEwLjE5LCBGaXhlZCBzbG9wZSBvZiBDMSA9IDQuNzddDQogICAgLVJhbmRvbSB0ZXJtcyAoQzEgaXMgYSBzbG9wZSBbZWZmZWN0cyBjb2RlZF0gLS41LC41KSAgICANCiAgICAgICAgLSBJZiB3ZSBkaWQgdGhpcyAoMStDMXxTdWJqZWN0cykgb3VyIENPViBtYXRyaXggd291bGQgbG9vayBsaWtlIHRoaXM6IA0KDQokJA0KXG1hdGhiZntDT1Y6IFN1Ymp9ID0gXGxlZnRbXGJlZ2lue2FycmF5fQ0KICAgICAgICAgIHtycnJ9DQogICAgICAgICAgSW50ZXJjZXB0ICYgY292KEl4U2xvcGUpIFxcDQogICAgICAgICAgY292KEl4U2xvcGUpICYgU2xvcGUgIFxcDQogICAgICAgICAgXGVuZHthcnJheX1ccmlnaHRdDQokJA0KDQotIEZvciBTdWJqZWN0cyB3ZSB3aWxsIGRvIChhc3N1bWUgMCBjb3JyZWxhdGlvbiBiZXR3ZWVuIGludGVyY2VwdC9zbG9wZSkNCg0KJCQNClxtYXRoYmZ7U3ViamVjdH0gPSBcbGVmdFtcYmVnaW57YXJyYXl9DQogICAgICAgICAge3Jycn0NCiAgICAgICAgICAyMy40NyAmIDAgXFwNCiAgICAgICAgICAwICYgMy45OCAgXFwNCiAgICAgICAgICBcZW5ke2FycmF5fVxyaWdodF0NCiQkDQoNCi0gRm9yIEl0ZW1zIHdlIHdpbGwgZG8gKGFzc3VtZSAwIGNvcnJlbGF0aW9uIGJldHdlZW4gaW50ZXJjZXB0L3Nsb3BlKQ0KDQokJA0KXG1hdGhiZntJdGVtc30gPSBcbGVmdFtcYmVnaW57YXJyYXl9DQogICAgICAgICAge3Jycn0NCiAgICAgICAgICAyLjE5NyAmIDAgXFwNCiAgICAgICAgICAwICYgNS4wMDkgIFxcDQogICAgICAgICAgXGVuZHthcnJheX1ccmlnaHRdDQokJCAgICANCiAgICAgICAgDQotIFNldHVwIG91ciBzaW11bGF0aW9ucyB0byBsZXQgdGhlIGNvcnJlbGF0aW9ucyB2YXJ5IGFyb3VuZCB6ZXJvOiANCg0KYGBge3J9DQojIGZpeGVkIGludGVyY2VwdCBhbmQgc2xvcGUNCmIgPC0gYygxMC4xOTEyLCA0Ljc3NzMpIA0KIyByYW5kb20gaW50ZXJjZXB0IGFuZCBzbG9wZSB2YXJpYW5jZS1jb3ZhcmlhbmNlIG1hdHJpeA0KIyBGb3IgU3ViamVjdA0KU3ViVkMgICA8LW1hdHJpeChjKDIzLjQ3MSwwLDAsMy45OCksIDIpDQojIEZvciBJdGVtcw0KSXRlbVZDIDwtIG1hdHJpeChjKDIuMTk3LDAsMCw1LjAwOSksIDIpIA0KIyBFeHJ0YWN0IHRoZSByZXNpZHVhbCBzZA0KcyA8LSA3LjEzXi41IA0KYGBgDQoNCi0gTmV4dCwgd2UgbmVlZCB0byBtYWtlIGEgbG1lciBvYmplY3QNCi0gd2UgbmVlZCB0byBmZWVkIGluIHRoZSBmaXhlZCBlZmZlY3RzLCByYW5kb20gZWZmZWN0cywgcmVzaWR1YWwsIGFuZCAiZnJhbWUiIG9mIHRoZSBkYXRhDQoNCmBgYHtyfQ0KU2ltTW9kZWwgPC0gbWFrZUxtZXIoRFYgfiBDb25kaXRpb24xICsgKENvbmRpdGlvbjF8U3ViamVjdCkrKENvbmRpdGlvbjF8SXRlbSksIA0KICAgICAgICAgICAgICAgICAgIGZpeGVmPWIsIFZhckNvcnI9bGlzdChTdWJWQyxJdGVtVkMpLCBzaWdtYT1zLCBkYXRhPVgpDQpzdW1tYXJ5KFNpbU1vZGVsKQ0KYGBgDQoNCi0gWW91IHdpbGwgbm90aWNlIHRoZSBTaW1Nb2RlbCBsb29rcyBsaWtlIG91ciByZWFsIGRhdGENCi0gVGhpcyBpcyB0aGUgbW9kZWwgaXQgaXMgZ29pbmcgdG8gcGFyYW1ldHJpY2FsbHkgc2ltdWxhdGUNCi0gSGVyZSBpcyBhbiBleGFtcGxlIG9mIDEgZGF0YXNldCBpdCB3aWxsIHNpbXVsYXRlIGdpdmVuIHRoZXNlIHBhcmFtZXRlcnMNCg0KYGBge3J9DQprYWJsZShoZWFkKGdldERhdGEoU2ltTW9kZWwpKSkgJT4lDQogIGthYmxlX3N0eWxpbmcoYm9vdHN0cmFwX29wdGlvbnMgPSBjKCJzdHJpcGVkIiwgImhvdmVyIiwgImNvbmRlbnNlZCIsICJyZXNwb25zaXZlIikpDQpgYGANCg0KIyMjIFBsb3QNCi0gT25lIHNpbXVsYXRpb24gZnJvbSBzaW1yIHBhY2thZ2UgYmFzZWQgb24gb3VyIHBhcmFtZXRlcnMNCg0KYGBge3IsIGVjaG89RkFMU0UsIGZpZy53aWR0aD04LjAsIGZpZy5oZWlnaHQ9My43NSxmaWcuc2hvdz0naG9sZCcsZmlnLmFsaWduPSdjZW50ZXInfQ0KbGlicmFyeShnZ3Bsb3QyKQ0KDQpTaW0xPC1nZXREYXRhKFNpbU1vZGVsKQ0KU2ltMSRTdWJqZWN0PC1hcy5mYWN0b3IoU2ltMSRTdWJqZWN0KQ0KU2ltMSRJdGVtPC1hcy5mYWN0b3IoU2ltMSRJdGVtKQ0KU2ltMSRDb25kaXRpb24xPC1hcy5mYWN0b3IoU2ltMSRDb25kaXRpb24xKQ0KDQp0aGVtZV9zZXQodGhlbWVfYncoYmFzZV9zaXplID0gMTIsIGJhc2VfZmFtaWx5ID0gIiIpKSANCmJ5U1MuQm94IDwtZ2dwbG90KGRhdGEgPSBTaW0xLCBhZXMoeCA9IFN1YmplY3QsIHk9RFYpKSsNCiAgZmFjZXRfZ3JpZChDb25kaXRpb24xfi4pKw0KICBnZW9tX3Zpb2xpbihhZXMoZmlsbD1TdWJqZWN0LCBjb2xvcj1TdWJqZWN0KSkrDQogIGdlb21fYm94cGxvdCh3aWR0aD0uMSkrDQogIHlsYWIoIlJlc3BvbnNlIikreGxhYigiU3ViamVjdCIpKw0KICBnZ3RpdGxlKCJCeSBTdWJqZWN0IikgKw0KICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAibm9uZSIpDQpieVNTLkJveA0KDQpieUl0ZW0uQm94IDwtZ2dwbG90KGRhdGEgPSBTaW0xLCBhZXMoeCA9IEl0ZW0sIHk9RFYpKSsNCiAgZmFjZXRfZ3JpZChDb25kaXRpb24xfi4pKw0KICBnZW9tX3Zpb2xpbihhZXMoZmlsbD1JdGVtKSkrDQogIGdlb21fYm94cGxvdCh3aWR0aD0uMSkrDQogIHlsYWIoIlJlc3BvbnNlIikreGxhYigiSXRlbSIpKw0KICBnZ3RpdGxlKCJCeSBJdGVtIikgKw0KICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAibm9uZSIpDQpieUl0ZW0uQm94DQpgYGANCg0KIyMgTW9udGUtQ2FybG8gU2ltdWxhdGlvbiANCi0gV2hhdCB3ZSB3YW50IHRvIGRvIGlzIHNpbXVsYXRlIHRoaXMgMTAwIHRpbWVzIHRvIGtlZXAgdGhlIGNvbXB1dGF0aW9uYWwgdGltZSBzaG9ydCAoYnV0IDEwMDAgaXMgdGhlIGRlZmF1bHQpDQotIEJ1dCB3ZSBuZWVkIHRvIGZpZ3VyZSBvdXQgd2hhdCB3ZSB3YW50IHRvIHRlc3QgYWJvdXQgb3VyIG1vZGVsIGFuZCBob3cNCiAgICAtIFdlIHdhbnQgdG8gdGVzdCBmaXhlZCBvciByYW5kb20gZWZmZWN0cz8gTGV0J3MganVzdCB3b3JyeSBhYm91dCBmaXhlZA0KICAgIC0gV2hpY2ggcHZhbHVlcyBkbyB3ZSB3YW50IHRvIHVzZT8gIA0KICAgICAgICAtIHosIHQsIEYgc2NvcmVzICh6LHQsZiksIExpa2VsaWhvb2QgcmF0aW8gdGVzdCAobHIpLCBLZW53YXJkLVJvZ2VyIChrciksIG9yIFBhcmFtZXRyaWMgYm9vdHN0cmFwIChwYik/DQotIEkgd2lsbCB0ZWxsIGl0IHRvIGdpdmUgbWUgdGhlIG9ic2VydmVkIHBvd2VyIGZvciB0aGUgZml4ZWQgZWZmZWN0IG9mIENvbmRpdGlvbiB1c2luZyBsciBtZXRob2QgKHRvIGJlIGZhc3RlciwgYnV0IHdpdGggYW4gYWxwaGEgLjA0NSwgc2luY2Ugd2UgaGF2ZSBzZWVuIGluIHRoZSBsYXN0IGZldyB3ZWVrcyB0aGF0IExpa2VsaWhvb2QgcmF0aW8gdGVzdGluZyB0ZW5kcyB0byB5aWVsZCB0eXBlIEkgZXJyb3Igc2xpZ2hseSBhYm92ZSAuMDUpICANCg0KYGBge3J9DQpTaW1Qb3dlcjE8LXBvd2VyU2ltKFNpbU1vZGVsLGZpeGVkKCJDb25kaXRpb24xIiwgImxyIiksDQogICAgICAgICAgICAgICAgICAgIG5zaW09MTAwLCBhbHBoYT0uMDQ1LCBwcm9ncmVzcz1GQUxTRSkNClNpbVBvd2VyMQ0KYGBgDQoNCi0gT2J2aW91c2x5LCB3ZSBoYXZlIGhpZ2ggcG93ZXIsIGJlY2F1c2UgdGhpcyBpcyAqT2JzZXJ2ZWQgUG93ZXIqDQoNCiMjIFVzaW5nIFZQQyBvdmVyIHJhdyBzY29yZXMNCi0gV2UgY2FuIHVzZSBvdXIgVlBDIG1lYXN1cmVzIHdlIGNhbGN1bGF0ZWQgYW5kIGdldCB0aGUgc2FtZSBhbnN3ZXINCg0KYGBge3J9DQpiMiA8LSBjKDAsIGQubWl4ZWQpICMgZml4ZWQgaW50ZXJjZXB0IGFuZCBzbG9wZQ0KU3ViVkMyICAgPC1tYXRyaXgoYyguNTYxNiwwLDAsLjA5NTI3KSwgMikNCkl0ZW1WQzIgPC0gbWF0cml4KGMoLjA1MjU2LDAsMCwuMTE5ODQpLCAyKSANCnMyIDwtICguMTcwNyleLjUgIyByZXNpZHVhbCBzZCANClNpbVZQQyA8LSBtYWtlTG1lcihEViB+IENvbmRpdGlvbjEgKyAoQ29uZGl0aW9uMXxTdWJqZWN0KSsoQ29uZGl0aW9uMXxJdGVtKSwgDQogICAgICAgICAgICAgICAgICAgZml4ZWY9YjIsIFZhckNvcnI9bGlzdChTdWJWQzIsSXRlbVZDMiksIHNpZ21hPXMyLCBkYXRhPVgpDQpTaW1Qb3dlci5WUEM8LXBvd2VyU2ltKFNpbVZQQyxmaXhlZCgiQ29uZGl0aW9uMSIsICJsciIpLA0KICAgICAgICAgICAgICAgICAgICAgICBuc2ltPTEwMCwgYWxwaGE9LjA0NSwgcHJvZ3Jlc3M9RkFMU0UpDQpTaW1Qb3dlci5WUEMNCmBgYA0KDQojIyMgQmxvY2sgY29ycmVsYXRpb25zIGluIE1vZGVsIEZpdHRpbmcNCi0gVG8gYmxvY2sgaGUgY29ycmVsYXRpb25zIHdlIG5lZWQgdG8gd3JpdGUgdGhlbSBvdXQgZGlmZmVyZW50bHkNCg0KYGBge3J9DQpiMiA8LSBjKDAsIGQubWl4ZWQpICMgZml4ZWQgaW50ZXJjZXB0IGFuZCBzbG9wZQ0KU3ViVkMyYSAgIDwtLjU2MTYNClN1YlZDMmIgICA8LS4wOTUyNw0KSXRlbVZDMmEgIDwtLjA1MjU2DQpJdGVtVkMyYiAgPC0uMTE5ODQNCnMyIDwtICguMTcwNyleLjUgIyByZXNpZHVhbCBzZCANClNpbVZQQ2EgPC0gbWFrZUxtZXIoRFYgfiBDb25kaXRpb24xICsgKENvbmRpdGlvbjF8fFN1YmplY3QpKyhDb25kaXRpb24xfHxJdGVtKSwgDQogICAgICAgICAgICAgICAgICAgZml4ZWY9YjIsIFZhckNvcnI9bGlzdChTdWJWQzJhLFN1YlZDMmIsSXRlbVZDMmEsSXRlbVZDMmIpLCBzaWdtYT1zMiwgZGF0YT1YKQ0KU2ltUG93ZXIuVlBDYTwtcG93ZXJTaW0oU2ltVlBDYSxmaXhlZCgiQ29uZGl0aW9uMSIsICJsciIpLA0KICAgICAgICAgICAgICAgICAgICAgICBuc2ltPTEwMCwgYWxwaGE9LjA0NSwgcHJvZ3Jlc3M9RkFMU0UpDQpTaW1Qb3dlci5WUENhDQpgYGANCg0KIyMgU2ltdWxhdGUgT2JzZXJ2ZWQgUG93ZXIgRGlyZWN0bHkNCi0gWW91IGNhbiBzaW1wbHkgY2FsbCB0aGUgbW9kZWwgd2UgYW5hbHl6ZWQgYW5kIGl0IHdpbGwgd29yaw0KDQpgYGB7cn0NClNpbVBvd2VyLkRpcmVjdDwtcG93ZXJTaW0oTWF4TW9kZWwsZml4ZWQoIkNvbmRpdGlvbjEiLCAibHIiKSwgDQogICAgICAgICAgICAgICAgICAgICAgICAgIG5zaW09MTAwLCBhbHBoYT0uMDQ1LCBwcm9ncmVzcz1GQUxTRSkNClNpbVBvd2VyLkRpcmVjdA0KYGBgDQoNCi0gU2luY2UgdGhlIHByb2dyYW0gbm90aWNlcyB5b3UgYXJlIGNhbGxpbmcgZnJvbSByZWFsIGRhdGEgaXRzIHdhcm5pbmcgeW91IHRoYXQgdGhpcyBtYXkgYmUgb2JzZXJ2ZWQgcG93ZXIuDQoNCiMjIFBvd2VyIEN1cnZlDQotIExldHMgc2F5IHdlIG5lZWQgdG8gZmlndXJlIG91dCBob3cgbWFueSBzdWJqZWN0cyBvciBpdGVtcyB3ZSB3b3VsZCB3YW50IHRvIGNvbGxlY3QgZm9yIGEgZnV0dXJlIHN0dWR5IGJhc2VkIG9uIG91ciBwaWxvdCBzdHVkeT8NCiAgICAtIFdoYXQgd2UgbmVlZCB0byBkbyBpcyByZXNpbXVsYXRlIG91ciBleHBlcmltZW50cywgYnV0IGV4cGFuZCBvdXQgdGhlIG51bWJlciBvZiBzdWJqZWN0cyBvciBpdGVtcw0KICAgIC0gQmFzaWNhbGx5IHdlIGhhdmUgdG8gY2hhbmdlIHRoZSBzYW1wbGUgc2l6ZSAob2YgaXRlbXMgb3Igc3ViamVjdHMpIGFuZCBydW4gYSBtb250ZS1jYXJsbyBzaW11bGF0aW9uIGVhY2ggdGltZS4gU28gYmFzZWQgb24gdGhlIG51bWJlciBvZiBzYW1wbGUgc2l6ZXMgeW91IHdhbnQgdG8gdGVzdCANCiAgICAgICAgLSBUaGlzIGlzIHZlcnkgY29tcHV0YXRpb25hbHkgZXhwZW5zaXZlIChTbG93KQ0KDQotIFRha2UgdGhlIHNlY29uZCBleGFtcGxlIGZyb20gQnJ5c2JhZXJ0ICYgU3RldmVucywgMjAxOCAgICAgIA0KLSBMZXQncyBmaXJzdCBqdXN0IGRvIHN1YmplY3RzIA0KICAgIC0gKm4qID0gIDIwLCA0MCwgNjAsIDgwICBbc28gb3VyIHNpbXVsYXRlZCBkYXRhIHNldCBtdXN0IGJlIGJ1aWx0IHdpdGggTiA9IDgwXQ0KICAgIC0gMjAgaXRlbXMNCiAgICAtIGFscGhhID0uMDQ1IChsciB0ZXN0aW5nKSANCiAgICAtICpkKiA9IC4xMTINCg0KYGBge3J9DQpJdGVtIDwtIGFzLmZhY3RvcihyZXAoMToyMCkpDQpTdWJqZWN0IDwtIGFzLmZhY3RvcihyZXAoMTo4MCkpDQpDb25kaXRpb24xPC1yZXAoLS41Oi41KQ0KWCA8LSBleHBhbmQuZ3JpZChTdWJqZWN0PVN1YmplY3QsSXRlbT1JdGVtLCBDb25kaXRpb24xPUNvbmRpdGlvbjEpDQpiMiA8LSBjKDAsIC4xMTIpIA0KU3ViVkMyICAgPC1tYXRyaXgoYyguMzY4LDAsMCwuMDA0KSwgMikNCkl0ZW1WQzIgPC0gbWF0cml4KGMoLjA2OCwwLDAsLjAwMSksIDIpIA0KczIgPC0gKC41NTkpXi41ICMgcmVzaWR1YWwgc2QgDQpTaW1DdXJ2ZSA8LSBtYWtlTG1lcihEViB+IENvbmRpdGlvbjEgKyAoQ29uZGl0aW9uMXxTdWJqZWN0KSsoQ29uZGl0aW9uMXxJdGVtKSwgDQogICAgICAgICAgICAgICAgICAgZml4ZWY9YjIsIFZhckNvcnI9bGlzdChTdWJWQzIsSXRlbVZDMiksIHNpZ21hPXMyLCBkYXRhPVgpDQpzdW1tYXJ5KFNpbUN1cnZlKQ0KYGBgDQoNCi0gVXNpbmcgdGhlICpwb3dlckN1cnZlKiBmdW5jdGlvbiB3ZSBjYW4gdGVzdCBhY3Jvc3Mgc3ViamVjdHMgDQoNCmBgYHtyfQ0KU0N1cnZlMTwtcG93ZXJDdXJ2ZShTaW1DdXJ2ZSwgZml4ZWQoIkNvbmRpdGlvbjEiLCAibHIiKSwNCiAgICAgICAgICAgICAgICAgICAgYWxvbmcgPSAiU3ViamVjdCIsDQogICAgICAgICAgICAgICAgICAgIGJyZWFrcyA9IGMoMjAsNDAsNjAsODApLA0KICAgICAgICAgICAgICAgICAgICBuc2ltPTEwMCxhbHBoYT0uMDQ1LCBwcm9ncmVzcz1GQUxTRSkNCnBsb3QoU0N1cnZlMSkNCmBgYA0KDQotIFRlc3QgYWNyb3NzIGl0ZW1zLCB3aGljaCB3aWxsIGNhbGN1bGF0ZSBmb3IgODAgc3ViZWN0cywgc28gZXhhbWluZSBsZXNzIGl0ZW1zDQoNCmBgYHtyfQ0KU0N1cnZlMjwtcG93ZXJDdXJ2ZShTaW1DdXJ2ZSwgZml4ZWQoIkNvbmRpdGlvbjEiLCAibHIiKSwNCiAgICAgICAgICAgICAgICAgICAgYWxvbmcgPSAiSXRlbSIsDQogICAgICAgICAgICAgICAgICAgIGJyZWFrcyA9IGMoNSwxMCwxNSksDQogICAgICAgICAgICAgICAgICAgIG5zaW09MTAwLGFscGhhPS4wNDUsIHByb2dyZXNzPUZBTFNFKQ0KcGxvdChTQ3VydmUyKQ0KYGBgDQoNCg0KLSBVc2luZyB0aGVzZSBzYW1lIHBhcmFtZXRlcnMgKE4gPSA4MCwgSXRlbXMgPSAyMCkgV2VzdGZhbGwgd2Vic2l0ZSB5aWVsZGVkIGEgcG93ZXIgb2YgLjg5NC4gVGhlIHNpbXVsYXRpb24gc3VnZ2VzdGVkIHBvd2VyIG9mIDk1JSwgd2l0aCBhIENJID0gWzg4LjcyIC0gOTguMzZdLiBTbyB0aGV5IHNlZW0gdG8gYWdyZWUgaW4gdGhpcyBjYXNlIChidXQgdGhleSBkaWQgbm90IGFncmVlIHdpdGggb3VyIGZpcnN0IGV4YW1wbGUsIGJ1dCB0aGF0IGVmZmVjdCBzaXplIHdhcyBodWdlKQ0KDQojIyBTaW11bGF0ZSBoaWdoZXIgb3JkZXIgaW50ZXJhY3Rpb25zDQotIFlvdSBjYW4gc2ltdWxhdGUgbW9yZSBjb21wbGV4IG1vZGVscyBhbmQgbW9yZSBjb21wbGV4IHRlcm1zLCBidXQgeW91IG11c3QgbWFwIG91dCB0aGUgbWF0cml4IG1vcmUgY2FyZWZ1bGx5DQotIFlvdSBoYXZlIHRvIGVzdGltYXRlIGZpeGVkIHNsb3BlcyAoQzEgKyBDMiArIEMxOkMxKQ0KLSBZb3UgaGF2ZSB0byBwcmVkZWZpbmUgYWxsIHlvdXIgcmFuZG9tIGVmZmVjdHMNCi0gaWYgd2UgYXNzdW1lIA0KICAgIC0gRm9yIHNpbXBsaWNpdHkgd2UgY2FuIGFzc3VtZSB6ZXJvIHJhbmRvbSBjb3JyZWxhdGlvbnMgdXNpbmcgYGRpYWdgIGNvbW1hbmQuIA0KICAgICAgICAtIHN1YmplY3QgZGlhZyhpbnRlcmNlcHQsIEMxIHNsb3BlLCBDMiBzbG9wZSwgQzE6QzIgc2xvcGUpIA0KDQpgYGB7ciwgZXZhbD1GQUxTRX0NCkl0ZW0gPC0gYXMuZmFjdG9yKHJlcCgxOjIwKSkNClN1YmplY3QgPC0gYXMuZmFjdG9yKHJlcCgxOjIwKSkNCkMxPC1yZXAoLS41Oi41KQ0KQzI8LXJlcCgtLjU6LjUpDQojIGNyZWF0ZXMgImZyYW1lIiBmb3Igb3VyIGRhdGENClggPC0gZXhwYW5kLmdyaWQoU3ViamVjdD1TdWJqZWN0LEl0ZW09SXRlbSwgQzE9QzEsQzI9QzIpDQoNCmIzIDwtIGMoMCwgLjA1LC0uMDUsLjEpICMgZml4ZWQgaW50ZXJjZXB0IGFuZCBzbG9wZQ0KU3ViVkMzICA8LWRpYWcoYyguMzUsLjAwNSwuMDA1LC4wMDUpKQ0KSXRlbVZDMyA8LWRpYWcoYyguMSwuMDA1LC4wMDUsLjAwNSkpICMgcmFuZG9tIGludGVyY2VwdCBhbmQgc2xvcGUgdmFyaWFuY2UtY292YXJpYW5jZSBtYXRyaXgNCnMzIDwtICgxLShzdW0oU3ViVkMzKStzdW0oSXRlbVZDMykpKV4uNSAjIHJlc2lkdWFsIHNkIA0KU2ltSW50ZXIgPC0gbWFrZUxtZXIoRFYgfiBDMSpDMiArIChDMSpDMnxTdWJqZWN0KSsoQzEqQzJ8SXRlbSksIA0KICAgICAgICAgICAgICAgICAgIGZpeGVmPWIzLCBWYXJDb3JyPWxpc3QoU3ViVkMzLEl0ZW1WQzMpLCBzaWdtYT1zMywgZGF0YT1YKQ0Kc3VtbWFyeShTaW1JbnRlcikNCg0KU2ltUG93ZXIuSW50ZXI8LXBvd2VyU2ltKFNpbUludGVyLGZpeGVkKCJDMTpDMiIsICJsciIpLA0KICAgICAgICAgICAgICAgICAgICAgICBuc2ltPTEwMCwgYWxwaGE9LjA0NSwgcHJvZ3Jlc3M9RkFMU0UpDQpTaW1Qb3dlci5JbnRlcg0KYGBgDQoNCiMgTm90ZXMNCi0gTGVhcm5pbmcgdGhlIHNpbXIgcGFja2FnZSBpcyBtdWNoIGVhc2llciB0aGFuIGxlYXJuaW5nIHRvIGNvbnN0cnVjdCB5b3VyIG93biBmdW5jdGlvbiB0byBjb25kdWN0IHBvd2VyIGFuYWx5c2lzIGZvciBtaXhlZCBtb2RlbHMNCi0gVGhlcmUgYXJlIG1hbnkgcGFyYW1ldGVycyB0byBlc3RpbWF0ZSBhbmQgQnJ5c2JhZXJ0ICYgU3RldmVucyAoMjAxOCkgc3VnZ2VzdCB3b3JraW5nIGZyb20gcGlsb3QgZGF0YSB0byBlc3RpbWF0ZSB0aGVzZSBwYXJhbWV0ZXJzIGJlZm9yZSBtb3ZpbmcgZm9yd2FyZC4gT3RoZXJ3aXNlIHdlIGhhdmUga25vdyB3YXkgdG8gZ3Vlc3Mgd2hhdCBpcyBnb2luZyBvbi4gIFRoZXJlIGlzIGN1cnJlbnRseSBubyB3b3JrIHRoYXQgSSBrbm93IG9mIHRoYXQgc2hvd3MgaG93IHBpbG90IHN0dWRpZXMgdXNpbmcgbWl4ZWQgbW9kZWxzIHdpbGwgcHJlZGljdCBmdXR1cmUgZWZmZWN0IHNpemUgcmF0ZXMvcG93ZXIuIA0KLSBNZXJnaW5nIFdlc3RmYWxscyBldCBhbC4ncyBtZXRob2QgdG8gZ2V0IFZQQyBhbmQgZXN0aW1hdGUgZCB3aXRoIHRoaXMgbW9udGUtY2FybG8gYXBwcm9hY2ggc2VlbXMgdXNlZnVsLiANCg0KDQojIFJlZmVyZW5jZXMNCg0KQnJ5c2JhZXJ0LCBNLiwgJiBTdGV2ZW5zLCBNLiAoMjAxOCkuIFBvd2VyIGFuYWx5c2lzIGFuZCBlZmZlY3Qgc2l6ZSBpbiBtaXhlZCBlZmZlY3RzIG1vZGVsczogQSB0dXRvcmlhbC4gKkpvdXJuYWwgb2YgQ29nbml0aW9uKiwgMSgxKS4NCg0KRmlzY2hlciwgUC4sIEtydWVnZXIsIEouIEkuLCBHcmVpdGVtZXllciwgVC4sIFZvZ3JpbmNpYywgQy4sIEthc3Rlbm0/bGxlciwgQS4sIEZyZXksIEQuLCAuLi4gJiBLYWluYmFjaGVyLCBNLiAoMjAxMSkuIFRoZSBieXN0YW5kZXItZWZmZWN0OiBhIG1ldGEtYW5hbHl0aWMgcmV2aWV3IG9uIGJ5c3RhbmRlciBpbnRlcnZlbnRpb24gaW4gZGFuZ2Vyb3VzIGFuZCBub24tZGFuZ2Vyb3VzIGVtZXJnZW5jaWVzLiAqUHN5Y2hvbG9naWNhbCBidWxsZXRpbiosIDEzNyg0KSwgNTE3Lg0KDQpHcmVlbiwgUC4sICYgTWFjTGVvZCwgQy4gSi4gKDIwMTYpLiBTSU1SOiBhbiBSIHBhY2thZ2UgZm9yIHBvd2VyIGFuYWx5c2lzIG9mIGdlbmVyYWxpemVkIGxpbmVhciBtaXhlZCBtb2RlbHMgYnkgc2ltdWxhdGlvbi4gKk1ldGhvZHMgaW4gRWNvbG9neSBhbmQgRXZvbHV0aW9uKiwgNyg0KSwgNDkzLTQ5OC4NCg0KSG9lbmlnLCBKLk0uICYgSGVpc2V5LCBELk0uICgyMDAxKSBUaGUgYWJ1c2Ugb2YgcG93ZXI6IHRoZSBwZXJ2YXNpdmUgZmFsbGFjeSBvZiBwb3dlciBjYWxjdWxhdGlvbnMgZm9yIGRhdGEgYW5hbHlzaXMuICpUaGUgQW1lcmljYW4gU3RhdGlzdGljaWFuKiwgNTUsIDE5LTI0Lg0KDQpKdWRkLCBDLiBNLiwgV2VzdGZhbGwsIEouLCAmIEtlbm55LCBELiBBLiAoMjAxNykuIEV4cGVyaW1lbnRzIHdpdGggbW9yZSB0aGFuIG9uZSByYW5kb20gZmFjdG9yOiBEZXNpZ25zLA0KYW5hbHl0aWMgbW9kZWxzLCBhbmQgc3RhdGlzdGljYWwgcG93ZXIuICpBbm51YWwgUmV2aWV3IG9mIFBzeWNob2xvZ3kqLCA2OCwgNjAxLTYyNS4gDQoNCldlc3RmYWxsLCBKLiwgS2VubnksIEQuIEEuLCAmIEp1ZGQsIEMuIE0uICgyMDE0KS4gU3RhdGlzdGljYWwgcG93ZXIgYW5kIG9wdGltYWwgZGVzaWduIGluIGV4cGVyaW1lbnRzIGluDQp3aGljaCBzYW1wbGVzIG9mIHBhcnRpY2lwYW50cyByZXNwb25kIHRvIHNhbXBsZXMgb2Ygc3RpbXVsaS4gKkpvdXJuYWwgb2YgRXhwZXJpbWVudGFsIFBzeWNob2xvZ3k6IEdlbmVyYWwqLA0KMTQzKDUpLCAyMDIwLTIwNDUuDQoNCjxzY3JpcHQ+DQogIChmdW5jdGlvbihpLHMsbyxnLHIsYSxtKXtpWydHb29nbGVBbmFseXRpY3NPYmplY3QnXT1yO2lbcl09aVtyXXx8ZnVuY3Rpb24oKXsNCiAgKGlbcl0ucT1pW3JdLnF8fFtdKS5wdXNoKGFyZ3VtZW50cyl9LGlbcl0ubD0xKm5ldyBEYXRlKCk7YT1zLmNyZWF0ZUVsZW1lbnQobyksDQogIG09cy5nZXRFbGVtZW50c0J5VGFnTmFtZShvKVswXTthLmFzeW5jPTE7YS5zcmM9ZzttLnBhcmVudE5vZGUuaW5zZXJ0QmVmb3JlKGEsbSkNCiAgfSkod2luZG93LGRvY3VtZW50LCdzY3JpcHQnLCdodHRwczovL3d3dy5nb29nbGUtYW5hbHl0aWNzLmNvbS9hbmFseXRpY3MuanMnLCdnYScpOw0KDQogIGdhKCdjcmVhdGUnLCAnVUEtOTA0MTUxNjAtMScsICdhdXRvJyk7DQogIGdhKCdzZW5kJywgJ3BhZ2V2aWV3Jyk7DQoNCjwvc2NyaXB0Pg0K
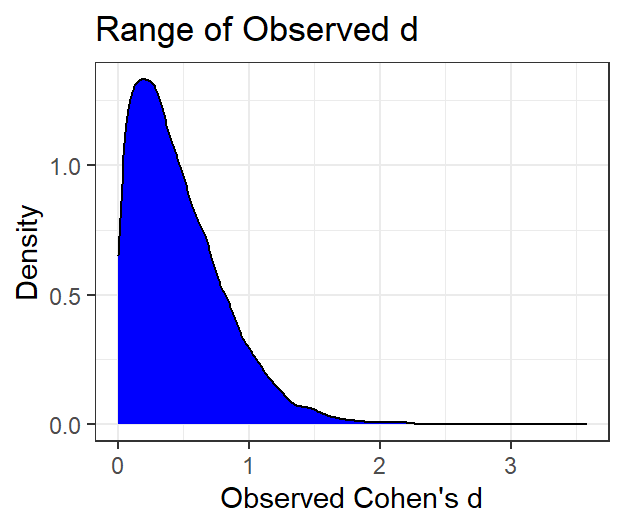 There is a long tail there which say you can easily think you have a big
effect.
There is a long tail there which say you can easily think you have a big
effect.


