Categorical Variables

Nominal Variables

• Things like gender or color (what we would have as factors in ANOVA)
  • We will assume (for now) that a subject can be a member of only one level of a factor a variable (i.e., you can blue or red, but not both)
• Decisions have to made on how to treat these variables in a regression
• There are three basic methods we will cover and how to interpret their effects and interactions
• Key to remember you are basically doing to t-tests, so you are always just comparing two things, but what those two things are will change as you change your coding (think the concept of contrasts in ANOVA from last semester)

Models with no Interactions (1 Nominal variable)

Dummy Coding

• The most common and basic type used (default in R if it senses a categorical variable)
• For each variable, you must assign a reference group (a baseline) for each variable
• Each group is compared to the reference group
• We ask the question, how much does each group deviate from the reference
• Here are two levels of one factor

Variable	C1
Happy	0
Sad	1

• Here are Three levels, but now you have to make 2 new variables
• Happy is the reference group

Variable	C1	C2
Happy	0	0
Sad	0	1
Mad	1	0

• Sad is the reference group

Variable	C1	C2
Happy	0	1
Sad	0	0
Mad	1	0

• Here are Four levels, but now you have to make 3 new variables
• Happy is the reference group

Variable	C1	C2	C3
Happy	0	0	0
Sad	0	0	1
Mad	0	1	0
Grumpy	1	0	0

Regression equation

• Two Levels: \(Y = B_1C1 + B_0\)
• Three Levels: \(Y = B_1C1 +B_2C2+ B_0\)
• Four Levels: \(Y = B_1C1 + B_2C2 + B_2C3 + B_0\)

Creating Dummy Variables

• In SPSS you would have to create dummy variables using Recode, but it R its a little easier
• In R, we have to convert our variable into a factor
  • R will default to alphabetical order
    • Sometimes easier to convert all your words into numbers (start with 0)
  • Next, convert your variable into a factor (as.factor)
    • Note: R calls dummy coding as contr.treatment
• First, let’s simulate a simple factor to work with
  • Emotion rating ~ Expressive intentions of the actor (0 = Flat, 1 = Normal, 2 = Exaggerated )
  • Three Levels: \(Emotion Rating = 0*Flat + 5*Normal +10*Exaggerated + 50 + \epsilon\)

Variable	C1	C2
Flat	0	0
Normal	1	0
Exaggerated	0	1

library(ggplot2)
#Set up simulation
set.seed(42)
N <- 200
X<- sample(rep(c(0,1,2),N),N,replace = FALSE)
Y <- 5*X + 50 + rnorm(N, sd=10)
Emotion.Data<-data.frame(Emotion=Y,Style=X)
qplot(Style,Emotion, data = Emotion.Data, colour = I("red"))+theme_bw()+geom_smooth(method='lm')

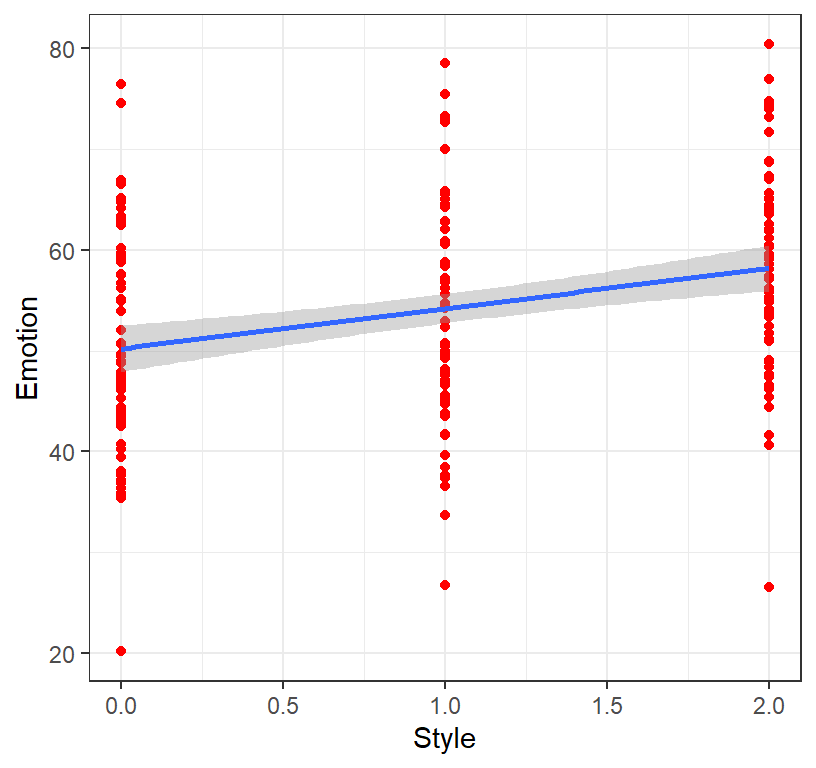
• If the data is already coded as 0, 1, 2 all we have to do is:

Emotion.Data$StyleF <- factor(Emotion.Data$Style,
                              level=c(0,1,2),
                              labels=c("Flat", "Normal", "Exaggerated"))

• We can re-plot it as violin/box plot to see our distributions (its a double-sided density plot [smoothed histogram])

ggplot(data = Emotion.Data,aes(StyleF,Emotion))+
  xlab("")+
  geom_violin(aes(fill=StyleF), trim = FALSE,adjust=1.5)+
  geom_boxplot(width=.1)+
  theme_bw()+
  theme(legend.position = "none")

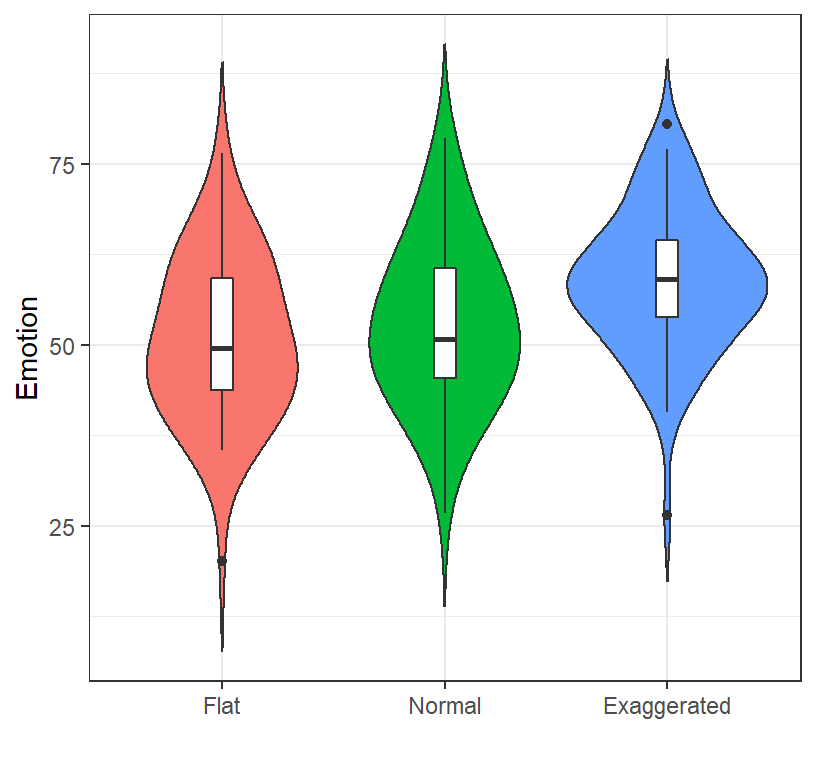
Interpret Regression

• Order of the factors matters
• Remember you are making each level of the variable a term in the equation as you have made a new variable for each level (except baseline)
• R make these dummy coded automatically so its easy to forget this
  • for 3 levels we will have 3 terms: intercept and StyleFNormal and StyleFExaggerated.

Model.1<-lm(Emotion ~ StyleF, data = Emotion.Data)

	Dependent variable:
	Emotion
Constant	50.798*** (1.273)
StyleFNormal	2.182 (1.828)
StyleFExaggerated	7.961*** (1.780)
Observations	200
R2	0.098
Adjusted R2	0.089
F Statistic	10.705*** (df = 2; 197)
Note:	p<0.05; p<0.01; p<0.001

Coefficients

• Intercept = Intercept of the equation (Which is the mean of Flat)
• StyleFNormal = coefficient (slope of Normal) from baseline (Flat)
• StyleFExaggerated = coefficient (slope of Exaggerated) from baseline (Flat)

Means per Condition

• Flat = Intercept
• Normal = Intercept + StyleFNormal
• Exaggerated = Intercept + StyleFExaggerated

Pvalues

• The pvalue on the intercept asks if the baseline (Flat) condition different from zero
• The pvalue on the slopes asks if each of the other levels is different from baseline (Flat)

Rotate the matrix

• What if we want to know if Normal is different from Exaggerated?
• We need to relevel (aka change what is zero)

Variable	C1	C2
Flat	1	0
Normal	0	0
Exaggerated	0	1

• We can fix that manually change what the baseline line level is with the relevel command in car package

Emotion.Data$StyleN<- relevel(Emotion.Data$StyleF, ref = "Normal")
Model.1.N<-lm(Emotion ~ StyleN, data = Emotion.Data)

• Notice in the table the labels and values have changed

	Dependent variable:
	Emotion
Constant	52.979*** (1.312)
StyleNFlat	-2.182 (1.828)
StyleNExaggerated	5.779** (1.809)
Observations	200
R2	0.098
Adjusted R2	0.089
F Statistic	10.705*** (df = 2; 197)
Note:	p<0.05; p<0.01; p<0.001

Contrast Coding

• Same contrasts as in our ANOVAs but there are two versions (unweighted and weighted) and both need to sum to zero
• We ask now a different question: How much does each group deviate from the mean of all groups
• I will review only the most common see for the others:
  • http://stats.idre.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/
• I will not show you the weighted version as not often used

Deviation Coding

• Note: R calls them Contrast Sums
• Let’s make the Flat the reference again

Variable	C1	C2
Normal	1	0
Exaggerated	0	1
Flat	-1	-1

• For deviatation code, R will use the LAST variable as references so we need to recode it by hand to be first as to match the order we want in the above table

Emotion.Data$Style.C.S <- factor(Emotion.Data$Style,
                              level=c(1,2,0),
                              labels=c("Normal", "Exaggerated", "Flat"))

• Then we will create our new contrast contr.sum with three levels (3)

contr.sum(3)

##   [,1] [,2]
## 1    1    0
## 2    0    1
## 3   -1   -1

• We will add that code to our lm function, by adding the parameters list(Style.C.S=contr.sum(3))

Model.1.CS<-lm(Emotion ~ Style.C.S, data = Emotion.Data,
               contrasts=list(Style.C.S=contr.sum(3)))

• Let’s look at how things differ from the mean of all conditions (grand mean)

	Dependent variable:
	Emotion
Constant	54.178*** (0.737)
Style.C.S1	-1.199 (1.057)
Style.C.S2	4.580*** (1.030)
Observations	200
R2	0.098
Adjusted R2	0.089
F Statistic	10.705*** (df = 2; 197)
Note:	p<0.05; p<0.01; p<0.001

• Intercept = Mean of means (grand mean)
• Mean of each condition calculated below

Mean.Interaction<-aggregate(Emotion~StyleF,data = Emotion.Data, FUN=mean)

StyleF	Emotion
Flat	50.79758
Normal	52.97930
Exaggerated	58.75829

• Grand mean calculated below

sum(aggregate(Emotion~StyleF,data = Emotion.Data, FUN=mean)[2])/3

## [1] 54.17839

Coefficients

• Style.C.S1 = coefficient on Normal as it differs from grand mean
• Style.C.S2 = coefficient on Exaggerated as it differs from grand mean
• To get the means for each condition:

Means per Condition

• Flat = Cannot get from this model
• Normal = Intercept + Style.C.S1
• Exaggerated = Intercept + Style.C.S2

Pvalues

• The pvalue on the intercept asks if the grand mean different from zero
• The pvalue on the slopes asks if each of the other levels is different from grand mean
• Note: We have lost the ability to ask about Flat condition, to get it back we would have to rotate the baseline and do it again

Simple Coding

• They must sum to zero, and the abs(values) must sum to 1
• Like in ANOVA you can design these to ask specific questions by merging conditions (or not)
• We will use the contr.treatment treatment (which R is using to automatically convert your categorical variables already)
• Just like dummy coding but we change the meaning of the intercept
• The reference level is First again

Variable	C1	C2
Flat	-1/3	-1/3
Normal	2/3	-1/3
Exaggerated	-1/3	2/3

Emotion.Data$Style.Simple <- factor(Emotion.Data$Style,
                              level=c(0,1,2),
                              labels=c("Flat", "Normal", "Exaggerated"))

Levels<-3
Simple.1<-contr.treatment(Levels) # Dummy code
#Make your codes
my.coding<-matrix(rep(1/Levels, Levels*(Levels-1)), ncol=Levels-1)
my.simple<-Simple.1-my.coding
my.simple

##            2          3
## 1 -0.3333333 -0.3333333
## 2  0.6666667 -0.3333333
## 3 -0.3333333  0.6666667

• We will add that code to our lm function, by adding the parameters list(Style.Simple=my.simple)

Model.1.Simple<-lm(Emotion ~ Style.Simple, data = Emotion.Data, 
                   contrasts=list(Style.Simple=my.simple))

	Dependent variable:
	Emotion
Constant	54.178*** (0.737)
Style.Simple2	2.182 (1.828)
Style.Simple3	7.961*** (1.780)
Observations	200
R2	0.098
Adjusted R2	0.089
F Statistic	10.705*** (df = 2; 197)
Note:	p<0.05; p<0.01; p<0.001

Coefficients

• This merges the dummy and deviance codings thus:
• Intercept = Mean of means (grand mean)
• StyleFNormal = slope of Normal from baseline (Flat)
• StyleFExaggerated = slope of Exaggerated from baseline (Flat)

Means per Condition

• You cannot get means of each condition from this model

Pvalues

• The pvalue on the intercept asks if the grand mean different from zero
• The pvalue on the slopes asks if each of the other levels is different from baseline (Flat)

Other types of contrast coding

• Helmert: compares each level to the mean of the subsequent levels [can be reversed]
• Forward Difference coding: one level is compared to the next (adjacent) level. (level 1 vs. 2. level 2 vs. 3) [can be reversed]
• Custom: Merge and compare levels at will

Center variables and test slopes

• There is no reason why you cannot treat the variables as continuous is they are ordinal
• just center them and treat like a continuous variable

Models with Interactions (2 Nominal variables)

• Interactions can be tricky as the interpretation depends on how you code IVs
  • First, let’s try some categorical vs. categorical interactions
• We will add a variable to our experiment from above; we will add the location where the actors work (Movie vs. Theatre)
• Emotion rating ~ Expressive intentions*location of the actor

\(Emotion = -3*Flat + 0*Normal +3*Exag +0*Movie - 1.5*Theatre - 0*Flat*Movie + 0*Normal*Movie +0*Exag*Movie - 10*Flat*Theatre +0*Normal*Theatre +10*Exag*Theatre + 50 + \epsilon\)

set.seed(42)
N <- 200
X <- sample(rep(c(-1,0,1),N),N,replace = FALSE)
Z <- sample(rep(c(0,1),N*3/2),N,replace = FALSE)

# Our equation to create Y
Y <- 3*X -1.5*Z+10*X*Z+ 50 + rnorm(N, sd=10)
#Built our data frame
Emotion.Data.2<-data.frame(Emotion=Y,Style=X,Location=Z)
Emotion.Data.2$Style<-Emotion.Data.2$Style+1

Dummy coding

• Lets dummy code all of them: convert them to a label in the other we want

# Convert all our factors
Emotion.Data.2$StyleF <- factor(Emotion.Data.2$Style,
                              level=c(0,1,2),
                              labels=c("Flat", "Normal", "Exaggerated"))

Emotion.Data.2$LocationF <- factor(Emotion.Data.2$Location,
                              level=c(0,1),
                              labels=c("Movie Set", "Theatre"))

-Let’s look at the collapsed means and the means per cell

Mean.Style<-aggregate(Emotion~StyleF,data = Emotion.Data.2, FUN=mean)
kable(Mean.Style)

StyleF	Emotion
Flat	43.13791
Normal	47.56490
Exaggerated	58.39412

Mean.Location<-aggregate(Emotion~LocationF,data = Emotion.Data.2, FUN=mean)
kable(Mean.Location)

LocationF	Emotion
Movie Set	49.75709
Theatre	49.99666

Mean.Interaction<-aggregate(Emotion~StyleF*LocationF,data = Emotion.Data.2, FUN=mean)
kable(Mean.Interaction)

StyleF	LocationF	Emotion
Flat	Movie Set	49.69693
Normal	Movie Set	45.80954
Exaggerated	Movie Set	53.42534
Flat	Theatre	34.00214
Normal	Theatre	49.26539
Exaggerated	Theatre	63.08686

• Let examine our regression, but we need to examine a main effects and interaction model

Model.I1.Dummy<-lm(Emotion ~ StyleF+LocationF, data = Emotion.Data.2)
Model.I2.Dummy<-lm(Emotion ~ StyleF*LocationF, data = Emotion.Data.2)

	Dependent variable:
	Emotion
	Main Effects	Interaction
	(1)	(2)
Constant	43.412*** (1.534)	49.697*** (1.592)
StyleFNormal	4.486* (1.987)	-3.887 (2.392)
StyleFExaggerated	15.319*** (1.936)	3.728 (2.333)
LocationFTheatre	-0.655 (1.604)	-15.695*** (2.462)
StyleFNormal:LocationFTheatre		19.151*** (3.513)
StyleFExaggerated:LocationFTheatre		25.356*** (3.423)
Observations	200	200
R2	0.253	0.427
Adjusted R2	0.242	0.412
F Statistic	22.170*** (df = 3; 196)	28.924*** (df = 5; 194)
Note:	p<0.05; p<0.01; p<0.001

• You will notice a large difference between the main effects and interaction model
• This is because the meaning coefficients in the interaction differ from the main effects model
• The main effects were explained above, but they change meaning a little because there is second variable

Main Effects

Coefficients

• These do not connect back to the individual cells as you are assuming the two factors have independent effects

  • Thus these are hypothetical values (not connected to the individual cells)

• Intercept = Estimate of the mean, assuming the two factors have independent effects at their 0 points [baseline]

• StyleFNormal = Normal - Flat (assuming the two factors are independent)

• StyleFExaggerated = Exaggerated - Flat (assuming the two factors are independent)

• LocationFTheatre = Theatre - Movie(assuming the two factors are independent)

• We can see the main effect models results

library(effects)
allEffects(Model.I1.Dummy)

##  model: Emotion ~ StyleF + LocationF
## 
##  StyleF effect
## StyleF
##        Flat      Normal Exaggerated 
##    43.09724    47.58320    58.41658 
## 
##  LocationF effect
## LocationF
## Movie Set   Theatre 
##  50.18653  49.53144

Means per Condition

• You cannot get them

Pvalues

• The pvalue on the intercept asks if the baseline is different from zero
• The pvalue on the differences asks if they are from different from baseline

Interactions

Coefficients

• These cells connect back to experimental cells
• Intercept = Location(0) @ Style(0) aka Movie @ Flat [real value]
• StyleFNormal = Differnce of [Location(0) @ Style(1)] - [Location(0) @ Style(0)]
• StyleFExaggerated = Differnce of [Location(0) @ Style(2)] - [Location(0) @ Style(0)]
• LocationFTheatre = Differnce of [Location(1) @ Style(0)] - [Location(0) @ Style(0)]
• StyleFNormal:LocationFTheatre = Differnce of [Location(1) @ Style(1)] - [Location(0) @ Style(1) - Location(0) @ Style(0) + [Location(1) @ Style(0)] - [Location(0) @ Style(0)]
• StyleFExaggerated:LocationFTheatre = Differnce of [Location(1) @ Style(2)] - [Location(0) @ Style(2) - Location(0) @ Style(0) + [Location(2) @ Style(0)] - [Location(0) @ Style(0)]

Means per Condition

• You can find all means for all cells!
• Flat @ Movie = Intercept
• Normal @ Movie = Intercept + StyleFNormal
• Exaggerated @ Movie = Intercept + StyleFExaggerated
• Flat @ Theatre = Intercept + LocationFTheatre
• Normal @ Theatre = Intercept + LocationFTheatre+StyleFNormal+StyleFNormal:LocationFTheatre
• Exaggerated @ Theatre = Intercept + LocationFTheatre + StyleFExaggerated + StyleFExaggerated:LocationFTheatre

Pvalues

• The pvalue on the intercept asks if the baseline is different from zero
• The pvalue on the differences asks if they are from different from baseline
• But these are now are now simple effects

Main effect model vs. Interaction model

• Since the results are not additive, the main effect model is useful only in which to understand how the terms have changed
• Gives some insight into the interaction

Graph Model

Inter.1<-effect("StyleF*LocationF", Model.I2.Dummy)
plot(Inter.1, multiline = TRUE)

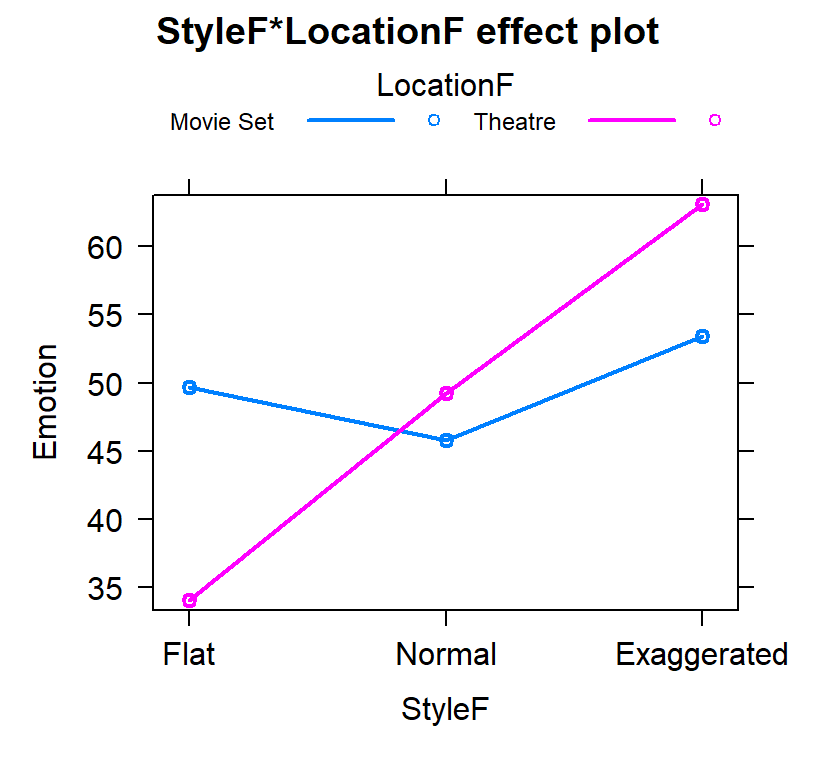
Connection to between-subject ANOVA

• Regression with only categorical variables can be converted into an ANOVA very easily
• Thus it can be treated just like ANOVA
• but the regression makes the ANOVA process moot as you can now the regression can be coded in such a way that you can test follow up tests in a way you want to test them all

library(car)
Anova(Model.I2.Dummy, type="III")

## Anova Table (Type III tests)
## 
## Response: Emotion
##                  Sum Sq  Df  F value    Pr(>F)    
## (Intercept)       96322   1 974.6213 < 2.2e-16 ***
## StyleF              941   2   4.7593  0.009598 ** 
## LocationF          4015   1  40.6229 1.316e-09 ***
## StyleF:LocationF   5814   2  29.4130 6.967e-12 ***
## Residuals         19173 194                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Note, we have to call for a Type III sum of squares to match SPSS output as R would default to Type I

Contrast Coding

Deviation Coding

• Lets code each variable as we did above

Emotion.Data.2$Style.C.S <- factor(Emotion.Data.2$Style,
                              level=c(1,2,0),
                              labels=c("Normal", "Exaggerated", "Flat"))
Emotion.Data.2$Location.C.S <- factor(Emotion.Data.2$Location,
                              level=c(1,0),
                              labels=c("Theatre", "Movie Set"))

Model.I1.C.S<-lm(Emotion ~ Style.C.S+Location.C.S, data = Emotion.Data.2, 
                 contrasts=list(Style.C.S=contr.sum(3),Location.C.S=contr.sum(2)))
Model.I2.C.S<-lm(Emotion ~ Style.C.S*Location.C.S, data = Emotion.Data.2,
                contrasts=list(Style.C.S=contr.sum(3),Location.C.S=contr.sum(2)))

• Let’s look at how things differ from the mean of all conditions (grand mean)

	Dependent variable:
	Emotion
	Main Effects	Interaction
	(1)	(2)
Constant	49.686*** (0.800)	49.214*** (0.707)
Style.C.S1	-2.116 (1.147)	-1.677 (1.011)
Style.C.S2	8.718*** (1.117)	9.042*** (0.985)
Location.C.S1	-0.328 (0.802)	-0.430 (0.707)
Style.C.S1:Location.C.S1		2.157* (1.011)
Style.C.S2:Location.C.S1		5.260*** (0.985)
Observations	200	200
R2	0.253	0.427
Adjusted R2	0.242	0.412
F Statistic	22.170*** (df = 3; 196)	28.924*** (df = 5; 194)
Note:	p<0.05; p<0.01; p<0.001

• Again we are testing between the grand mean and the individual terms

Main Effects

Coefficients

• These do not connect back to the individual cells as you are assuming the two factors have independent effects
• Thus these are hypothetical Grand mean values
• Intercept = Grand Mean, but assuming the two factors have independent effects
• Style.C.S1 = Normal (averaged over location) - Grand Mean (assuming the two factors are independent)
• Style.C.S2 = Exaggerated (averaged over location) - Grand Mean (assuming the two factors are independent)
• Location.C.S1 = Theatre (averaged over Style) - Grand Mean (assuming the two factors are independent)

Means per Condition

• Cannot get from this model

Pvalues

• The pvalue on the intercept asks if the baseline (Grand Mean) is different from zero
• The pvalue on the slopes asks if each of the other levels is different from the baseline (Grand Mean)
• Note we are missing tests on Flat and Movie cell, we would need to rotate the matrix and run again

Interactions

Coefficients

• Intercept = Grand Mean (all 6 cells mean averaged)
• Style.C.S1 = Normal (averaged over location) from Grand Mean
• Style.C.S2 = Exaggerated (averaged over location) from Grand Mean
• Location.C.S1 = Theatre (averaged over Style) from Grand Mean
• Style.C.S1:Location.C.S1 = difference of Normal @ Theatre from Grand Mean
• Style.C.S2:Location.C.S1 = difference of Exaggerated @ Theatre from Grand Mean

Means per Condition

• Cannot get from this model

Pvalues

• The pvalue on the intercept asks if the baseline (Grand Mean) is different from zero
• The pvalue on the differences asks if each of the other levels is from the (Grand Mean)
• Note we are missing tests on Flat and movie cell, we would need to rotate the matrix and run again

Models with Interactions (1 Nominal and 1 Continuous Variable)

• We will change our experiment from above, we will add a likert scale which the actor rates how “good” they think the performance was [-3 terrible to 3 excellent]
• Emotion rating ~ Quality Rating X location of the actor (i.e., Movie Set, Theatre)

#Set up simulation
set.seed(42)
N <- 200
X <- runif(N,-3,3)
Z <- sample(rep(c(0,1),N/2),N,replace = FALSE)
# Our equation to create Y
Y <- 4*X +2*Z+8*X*Z+ 50 + rnorm(N, sd=10)
#Built our data frame
Emotion.Data.3<-data.frame(Emotion=Y,Quality=X,Location=Z)

Center the continuous variable

• Best to center as its will help us interpret

# Convert all our factors
Emotion.Data.3$Quality.C <- scale(Emotion.Data.3$Quality, scale = FALSE)[,]

Dummy coding of our nominal variable

• Make Location into a factor

# Convert all our factors
Emotion.Data.3$LocationF <- factor(Emotion.Data.3$Location,
                                   level=c(0,1),
                                   labels=c("Movie Set","Theatre"))

• First to understand what the interaction will yield lets us run two regressions where we seperate our factor to see what the slopes would be just for actors at Movie Set vs at the Theatre

Movie Set ONLY vs Theatre Only

• We will subset the data and test for the Quality slopes

Model.Movie<-lm(Emotion ~ Quality.C, 
                data = subset(Emotion.Data.3,LocationF=="Movie Set"))
Model.Theatre<-lm(Emotion ~ Quality.C, 
                data = subset(Emotion.Data.3,LocationF=="Theatre"))

	Dependent variable:
	Emotion
	Movie Set ONLY	Theatre Only
	(1)	(2)
Constant	50.468*** (0.976)	52.426*** (1.051)
Quality.C	4.551*** (0.593)	12.083*** (0.569)
Observations	100	100
R2	0.375	0.821
Adjusted R2	0.369	0.819
F Statistic (df = 1; 98)	58.842***	450.430***
Note:	p<0.05; p<0.01; p<0.001

• Ignore the intercepts and pay attention to the slopes:
  • Quality @ the Movie Set ONLY is \(b\)= 4.551
    • The pvalues tells you if the slope of quality is differnet from a slope of 0
      
  • Quality @ the Theatre Only ONLY is \(b\)= 12.083
    • The pvalues tells you if the slope of quality is differnet from a slope of 0
      
• What we really want to test is if there is a difference in slopes between quality at Movies sets VS Theatre

Testing the Interaction

• We will test a main effects model, Quality+Location and compare it to an interaction model Quality*Location

Model.E3.1<-lm(Emotion ~ Quality.C+LocationF, data = Emotion.Data.3)
Model.E3.2<-lm(Emotion ~ Quality.C*LocationF, data = Emotion.Data.3)

• Does model interaction improve the model fit? (Just like we did with hierarchical testing)

Model.Fit.E3<-anova(Model.E3.1,Model.E3.2)

library(knitr)
kable(Model.Fit.E3)

Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
197	28691.61	NA	NA	NA	NA
196	20141.73	1	8549.886	83.19931	0

• Yes! The interaction is significant improvement
• Let’s go examine the individual regression paramaters:

Interpret Regression

	Dependent variable:
	Emotion
	Main Effects	Interaction
	(1)	(2)
Constant	50.513*** (1.207)	50.468*** (1.014)
Quality.C	8.749*** (0.488)	4.551*** (0.616)
LocationFTheatre	1.948 (1.707)	1.958 (1.434)
Quality.C:LocationFTheatre		7.532*** (0.826)
Observations	200	200
R2	0.621	0.734
Adjusted R2	0.617	0.730
F Statistic	161.308*** (df = 2; 197)	180.143*** (df = 3; 196)
Note:	p<0.05; p<0.01; p<0.001

Main Effects Model

• Intercept = Mean of Quality @ Movies [p = Is the intercept different from 0]
• Quality.C = Quality.C slope averaged across Movies & * Threatre*
  • This is a Main Effect [p = Is slope different from 0 slope]
    • This would almost be like averaging the slopes from our Movie Set ONLY and Theatre Only Models
      • \(b\) = (4.551 + 12.083)/2 = 8.317
• LocationFTheatre = Threatre difference from intercept [p = Is mean of Theatre different from Movies @ mean of quality]
  • This is a Simple Effect

Interaction Model

• Intercept = Mean of Quality @ Movies [p = Is the intercept different from 0]
• Quality.C = Quality.C slope @ Movies
  • This is a Simple Slope [p = Is slope different from 0 slope]
    • To prove it we can see it matches the slopes from our Movie Set ONLY Model, \(b\)= 4.551
• LocationFTheatre = Threatre difference from intercept [p = Is mean of Theatre different from movies @ mean of quality]
  • This is a Simple Effect
• Quality.C:LocationFTheatre= slope difference between Movie and Theatre [p = Is the slope of quality @ Theatre different from slope at ]
  • This is an Interaction
    • To prove it we can see it matches the slopes of Theatre Only - Movie Set ONLY Model
      • \(b\)= (12.083 - 4.551) = 7.532
• If you wanted to know the simple slope of Theatre Only you would have to relevel Location and make Theatre = 0 (i.e., the reference)

Emotion.Data.3$LocationT<- relevel(Emotion.Data.3$LocationF, ref = "Theatre")
Model.E3.2.ReLevel<-lm(Emotion ~ Quality.C*LocationT, data = Emotion.Data.3)

	Dependent variable:
	Emotion
	Theatre is Ref
Constant	52.426*** (1.014)
Quality.C	12.083*** (0.549)
LocationTMovie Set	-1.958 (1.434)
Quality.C:LocationTMovie Set	-7.532*** (0.826)
Observations	200
R2	0.734
Adjusted R2	0.730
F Statistic	180.143*** (df = 3; 196)
Note:	p<0.05; p<0.01; p<0.001

• You will notice the interaction flipped direction and now the Quality.C coefficient \(b\) = 12.083 = the Theatre Only model \(b\) = 12.083

Plotting Interaction

• Often times you will need to use the effects package and plot by hand
• The rockchalk package will work for simple models like this one

library(rockchalk)
plotSlopes(Model.E3.2, plotx = "Quality.C", modx = "LocationF")

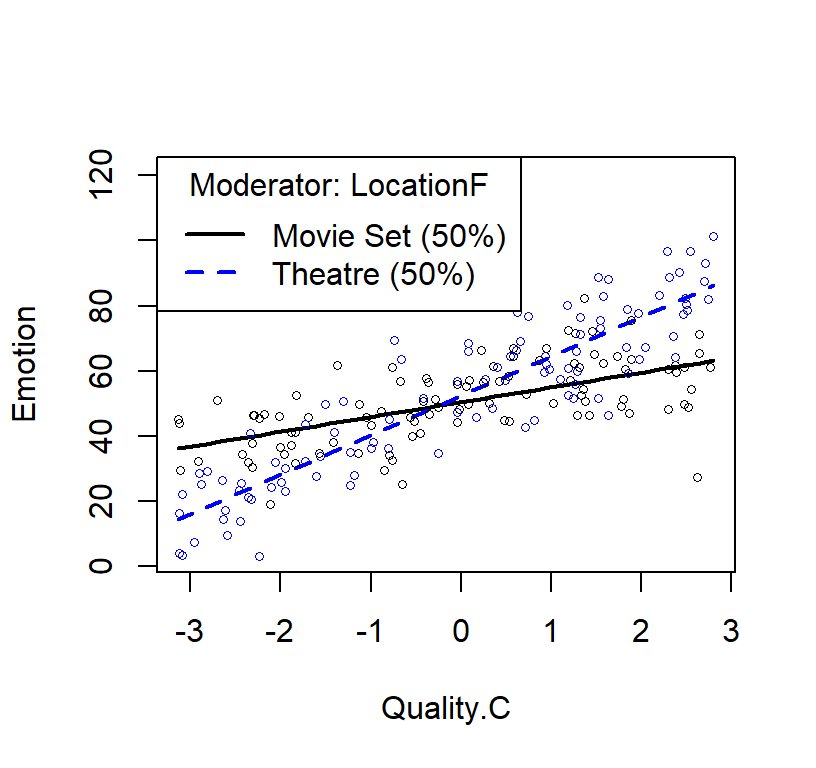
Deviation coding of our nominal variable

• We will still center quality
• This creates a more ANOVA like interpretation of the interaction

Emotion.Data.3$LocationD <- factor(Emotion.Data.3$Location,
                                   level=c(1,0),
                                   labels=c("Theatre","Movie Set"))
Model.E3.D1<-lm(Emotion ~ Quality.C+LocationD, data = Emotion.Data.3,
                 contrasts=list(LocationD=contr.sum(2)))
Model.E3.D2<-lm(Emotion ~ Quality.C*LocationD, data = Emotion.Data.3,
                 contrasts=list(LocationD=contr.sum(2)))

Interpret Regression

	Dependent variable:
	Emotion
	Main Effects	Interaction
	(1)	(2)
Constant	51.487*** (0.853)	51.447*** (0.717)
Quality.C	8.749*** (0.488)	8.317*** (0.413)
LocationD1	0.974 (0.853)	0.979 (0.717)
Quality.C:LocationD1		3.766*** (0.413)
Observations	200	200
R2	0.621	0.734
Adjusted R2	0.617	0.730
F Statistic	161.308*** (df = 2; 197)	180.143*** (df = 3; 196)
Note:	p<0.05; p<0.01; p<0.001

Main Effects

Coefficients & Pvalues

• Intercept = Mean of Quality @ mean of Movie & Theatre (imaginary) [p = Is the intercept different from 0]
• Quality.C = Quality.C slope [p = Is slope different from 0]
• LocationFTheatre = Threatre difference from 0 (not - 1) thus is 1/2 the slope of the dummy code [p = Is mean of Theatre different from movies @ mean of quality]

Interactions

Coefficients & Pvalues

• Intercept = Mean of Quality @ mean of Movie & Theatre (imaginary) [p = Is the intercept different from 0]
• Quality.C = Quality.C slope @ mean of Movie & Theatre (imaginary) [p = Is the Main effect of quality @ mean of Movie & Theatre]
• LocationFTheatre = Threatre difference from intercept [p = Is the Main effect of Location @ mean of quality]
• Quality.C:LocationFTheatre= Quality.C slope difference between Movie and theatre [p = Is the interaction]
• Note all coefficients are 1/2 of the size they should be!

Simple coding of our nominal variable

• We will still center quality
• This creates a more ANOVA-like interpretation of the interaction,
  • Most importantly it does not screw up our coefficients as they match the dummy code values (which make the most sense)
• This time I will hand code it into a factor (easy with only 2 levels)

Emotion.Data.3$LocationS<-as.numeric(Emotion.Data.3$Location)-.5
Model.E3.S1<-lm(Emotion ~ Quality.C+LocationS, data = Emotion.Data.3)
Model.E3.S2<-lm(Emotion ~ Quality.C*LocationS, data = Emotion.Data.3)

Interpret Regression

	Dependent variable:
	Emotion
	Main Effects	Interaction
	(1)	(2)
Constant	51.487*** (0.853)	51.447*** (0.717)
Quality.C	8.749*** (0.488)	8.317*** (0.413)
LocationS	1.948 (1.707)	1.958 (1.434)
Quality.C:LocationS		7.532*** (0.826)
Observations	200	200
R2	0.621	0.734
Adjusted R2	0.617	0.730
F Statistic	161.308*** (df = 2; 197)	180.143*** (df = 3; 196)
Note:	p<0.05; p<0.01; p<0.001

Main Effects

Coefficients & Pvalues

• Intercept = Mean of Quality @ mean of Movie & Theatre (imaginary thing) [p = Is the intercept different from 0]
• Quality.C = Quality.C slope [p = Is slope different from 0]
• LocationFTheatre = Threatre difference from 0 [p = Is mean of Theatre different from movies @ mean of quality]

Interactions

Coefficients & Pvalues

• Intercept = Mean of Quality @ mean of Movie & Theatre (imaginary thing) [p = Is the intercept different from 0]
• Quality.C = Quality.C slope @ mean of Movie & Theatre (imaginary thing) [p = Is the Main effect of quality @ mean of Movie & Theatre]
• LocationS = Threatre difference from intercept [p = Is the Main effect of Location @ mean of quality]
• Quality.C:LocationS= Quality.C slope difference between Movie and theatre [p = Is their an interaction]
• Note all coefficients are their proper size now (to match true differences)
• Best option is often dummy or simple, deviation here is weird