Repeated Factors

Note: Much the code used to generate the results seen to today appears in the rmd file, but not in here. You can dowload the rmd file to see the code, you will see echo=FALSE, which hides the code.

Crossed Designs

• The simplest design is 1 factor (2 levels) where each person responds to both levels (1 time)
• For example, everyone sees 1 stimulus and is told that person is A) friend and B) Foe

Subject	Stimuli 1
1	AB
2	AB

• These are analyzed typically as paired samples t-test

• A more complex design is 1 factor (2 levels) where each person responds to both levels (A & B) but with multiple stimuli (to test multiple trials):

• Fully Crossed Design - As above, all subjects see all experimental conditions (A & B) and stimuli (1 & 2)

Subject	Stimuli 1	Stimuli 2
1	AB	AB
2	AB	AB

• What if we have order effects? There are lots of solutions:

• Counterbalanced Designs - As above, all subjects saw all experimental conditions (A & B), and stimuli (1 & 2) but balanced across condition (the idea is that when we take means across our stimuli carryover washout)

Subject	Stimuli 1	Stimuli 2
1	A	B
2	B	A

Classical Solutions

• As designs get more and more complex (more conditions, more stimuli, repeated trials of stimuli within conditions), we have to be careful about how we design studies so we can track condition vs stimuli effects
• The main problem is that subject scores tend to correlate with themselves (which is the whole point of repeated designs), but they also tend to change over repeated trials (fatigue, boredom, order effects, etc)
  • In GLM (ANOVA/t-tests) we simply averaged over stimuli because most of us were taught to use a Latin squares designs (balanced type of counterbalancing) to average out all these problems
  • Now it seems because of the ease of randomizing trials, often researchers just prefer to run lot of random trials in random orders hoping things will wash out
  • Randomization is not a subsite for counterbalancing simply because you cannot “know” what is causing the variance.

Mixed Models Solutions

• Mixed models allow for you to start to deal with more complex designs and track order effects or other issues
• To benefit from these statistics you need to start collecting multiple trials, stimuli or both!
• You also open up more designs, as we can start to control for stimuli (or trial order effects)

Stimuli-within-condition design - As above, all subjects see all experimental conditions (A & B), and stimuli (1 & 2) but stimuli are nested into condition. You will have carry-over effects, but you can have stimuli level random effects

Subject	Stimuli 1	Stimuli 2	Stimuli 3	Stimuli 4
1	A	A	B	B
2	A	A	B	B
3	B	B	A	A
4	B	B	A	A

• We will return to item/stimuli/trial effects in a few weeks. today we will focus on first step of dealing with repeated measure data

See Westfall, Kenny, & Judd, 2014 for a more detailed explanation and for discussion about power for mixed models. I have summarized the some of the designs of interest they talk about

Correlated Measures

• When subjects repeat trials or do multiple conditions, their scores tend to be correlated
  • We want to control for individual subject variability
  • In the formula below, we remove the shared variance from the standard error as measured by Pearson’s r between conditions

\[t = \frac{M_1-M_2}{\sqrt{\frac{S_1^2 + S_2^2}{n}-\frac{2rS_1S_2}{n}}}\]

1 Factor: 2 Level Designs

• Normally we collect 1 trial per condition and test between the means, or we collect multiple trials and average between trials and run the paired sample t-test above
• Let’s run a simulation of that kind of study
• Also, we must assume a specific covariance matrix, where, \(\sigma^2 = 4\)

\[ \mathbf{Cov} = \sigma^2\left[\begin{array} {rrr} 1 & .4 \\ .4 & 1 \\ \end{array}\right] \]

• We will set \(n\) = 12, \(r\) =.4, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2\) = 4

set.seed(666)
library(tidyr)
library(dplyr)
library(MASS)
n = 12 ; r = .4 ; M1=2; M2=4; S2=4
# Generate Cov matrix
SigmaMatrix<-matrix(c(1,r, 
                      r,1), nrow=2, ncol=2)*S2

DataSim1 = mvrnorm(n=n, mu=c(M1, M2), Sigma=SigmaMatrix, empirical=TRUE)
colnames(DataSim1) <- c("None","Some")
DataSim1<-gather(data.frame(DataSim1),key = "Chocolate", value = "Attention")
DataSim1$SS<-as.factor(rep(seq(1:n),2))

Plot of Simulation 1

• Spagetti plot per person

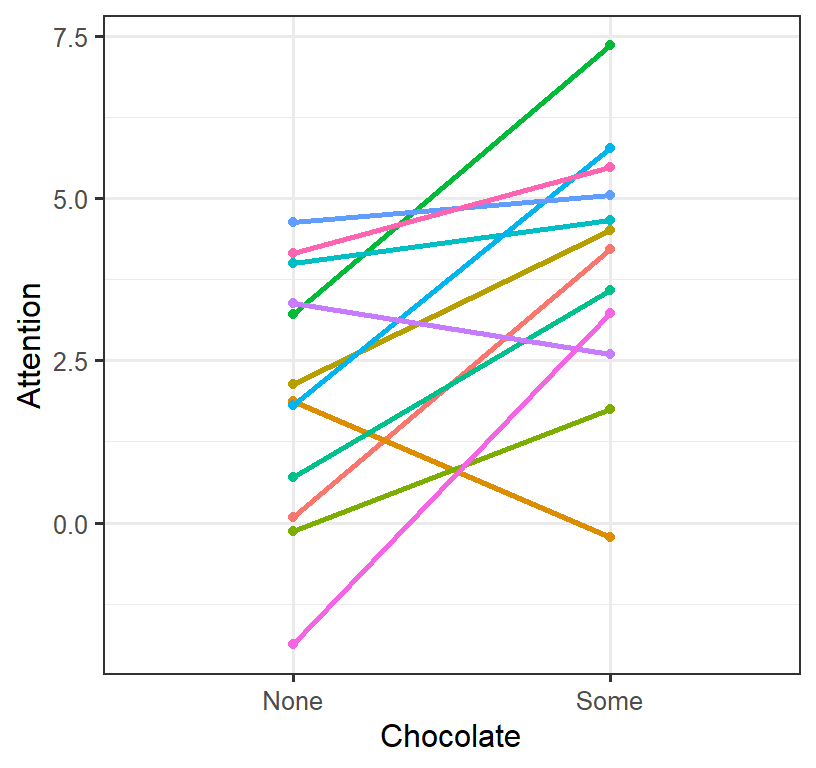
Paired t-test

T1<-t.test(Attention~Chocolate, paired=TRUE,DataSim1)
library(apa)
cat(apa(T1, format = "rmarkdown", print = FALSE))

t(11) = -3.16, p = .009, d = -0.91

• Note: t-test in R does M1-M2 (so it reported it negative),
• Also, our \(r\) = .4 between None and Some Chocolate, had we set it to zero, this paired test would be equal to a between-subjects t-test [in a perfect world (with no variance) \(r\) = 1]

Mixed: Random Intercepts

• We can mirror this result using our mixed regression
• In this case, to match the paired-sample t-test, we need to let the intercept vary per subject

library(lme4)
Model.1<-lmer(Attention~Chocolate
               +(1|SS),
               data=DataSim1, REML=FALSE)
summary(Model.1, correlation=FALSE)

## Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
##   method [lmerModLmerTest]
## Formula: Attention ~ Chocolate + (1 | SS)
##    Data: DataSim1
## 
##      AIC      BIC   logLik deviance df.resid 
##    105.2    109.9    -48.6     97.2       20 
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.00520 -0.55683  0.02367  0.75042  1.38076 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  SS       (Intercept) 1.467    1.211   
##  Residual             2.200    1.483   
## Number of obs: 24, groups:  SS, 12
## 
## Fixed effects:
##               Estimate Std. Error      df t value Pr(>|t|)   
## (Intercept)     2.0000     0.5528 20.6897   3.618  0.00164 **
## ChocolateSome   2.0000     0.6055 12.0000   3.303  0.00631 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• You will notice that the t-values pretty much match
• The model is removing the intercept differences between the subjects
• We can plot the prediction of the model per person for both fixed + random and fixed alone

DataSim1$FR<-predict(Model.1)  #Fixed + random
DataSim1$Fixed<-predict(Model.1,re.form=NA) # Fixed only

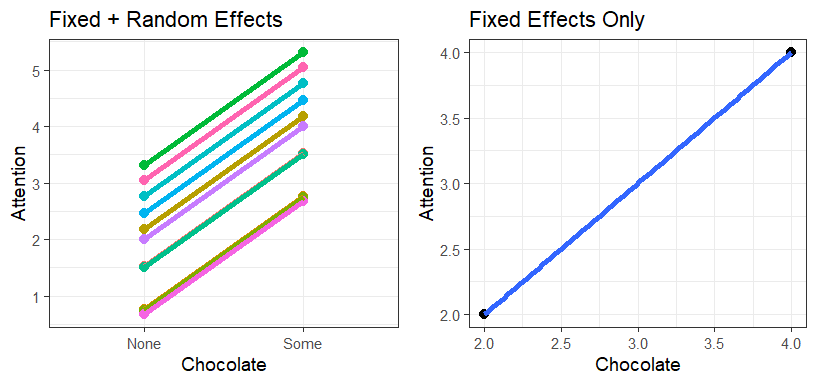
• You will notice that we did not account for the random slopes

Rm.t.test.plot <-ggplot(data = DataSim1, aes(x = Chocolate, y=Attention,group=SS))+
  facet_wrap(~SS)+
  geom_point(aes(colour = SS))+
  geom_smooth(method = "lm", se = FALSE, aes(group=SS,colour = SS))+
  ylab("Attention")+xlab("Chocolate")+
  theme(legend.position = "none")
Rm.t.test.plot

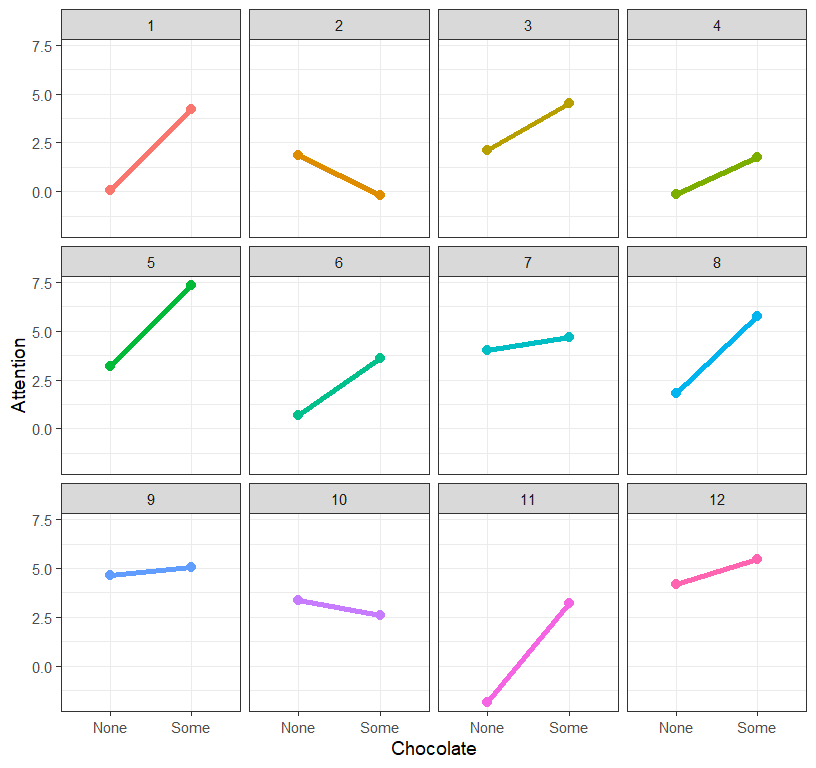- Its clear that each subject is affected by Chocolate in a different way, so we should try to account for the slope differences - We did with this school in MLM, so we must be able to do it here!

Model.1a<-lmer(Attention~Chocolate
               +(1+Chocolate|SS),
               data=DataSim1, REML=FALSE)

Error: number of observations (=24) <= number of random effects (=24) for term (1 + Chocolate | SS); the random-effects parameters and the residual variance (or scale parameter) are probably unidentifiable

• What is this crazy message? Well, it’s telling us we are trying we cannot do this. Why?
  • Well, how variance do you have round the estimate of the slope do you have per subject?
• How can you estimate any variance around the slope if you have only 1 slope per subject?
  • You need to have multiple estimates per subject per condition!
    • The more trials we have per subject, the better estimate of the slope and we can calculate the variance around that slope!

Mixed: Random Intercepts & Slopes

• Let’s add more trials per condition: Simulation 2
• However, things get more complicated
  • How much measurement error is there when re-measurement of the same condition per subject?
    • Could that value differ per trial or condition?
    • Is it the same stimulus or a new one?
      • Could the new stimulus be having an effect?
      • We will assume a repeat of the same stimulus per condition
  • What is the variance of each condition?
    • They can differ (ANOVA assumptions say they cannot)
      • If we did have multiple stimuli per condition could they vary as a function of the condition?
• To understand all the levels of variance let’s simulate the chocolate study with 4 trials of two conditions:

Simulation 2a: No Variance

• We will set \(n\) = 4, Trials=4, \(r\) = .6, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 0, \(\sigma^2_{M2}\) = 0, \(\sigma^2_{measurement}\) = 0

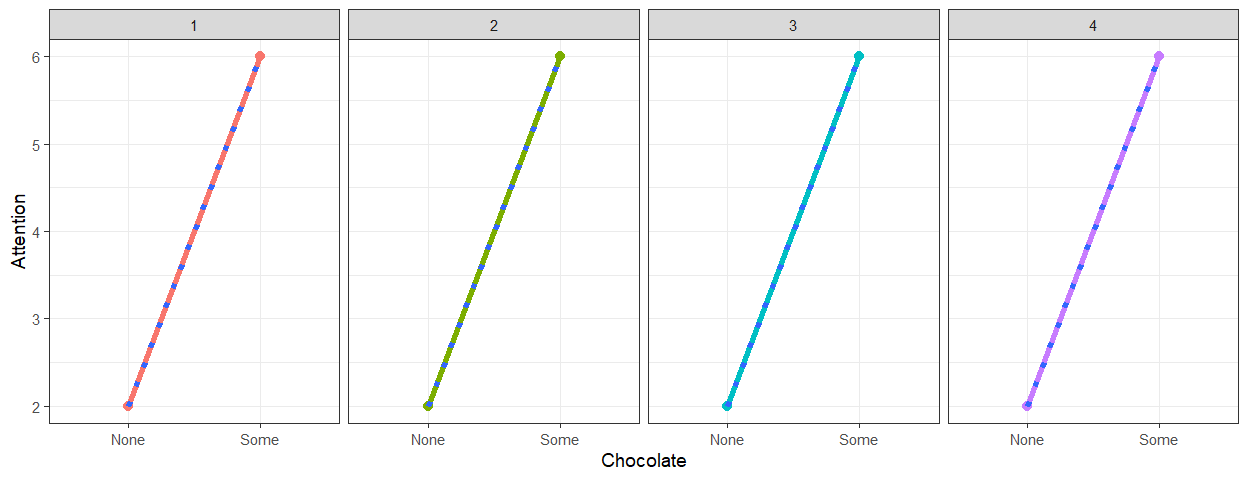
Simulation 2b: Measurement Error

• We will set \(n\) = 4, Trials=4, \(r\) = .6, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 0, \(\sigma^2_{M2}\) = 0, \(\sigma^2_{measurement}\) = 4

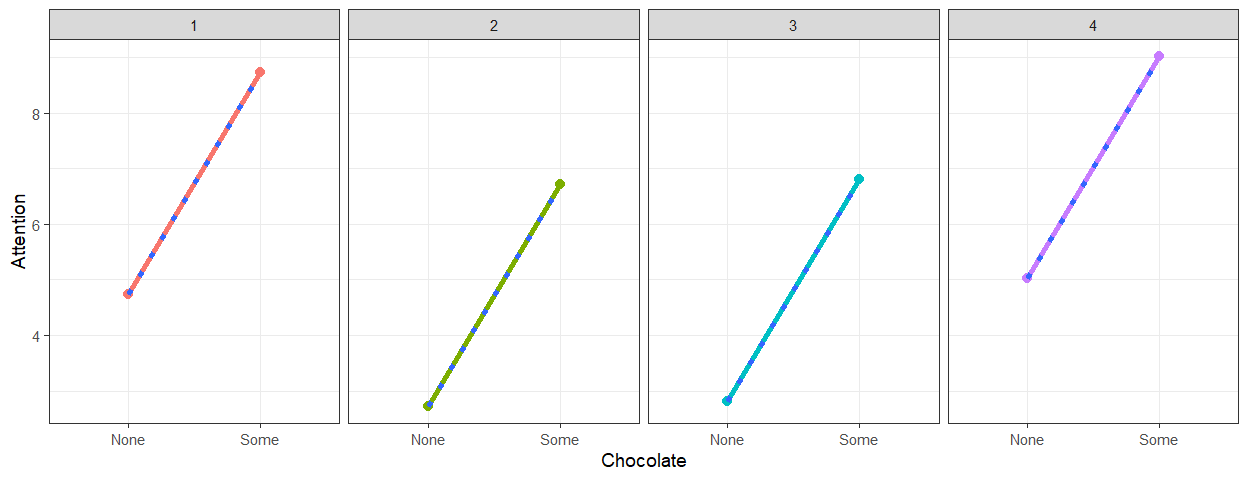
Simulation 2c: Intercept Variance

• We will set \(n\) = 4, Trials=4, \(r\) = NA, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 4, \(\sigma^2_{M2}\) = 0, \(\sigma^2_{measurement}\) = 0

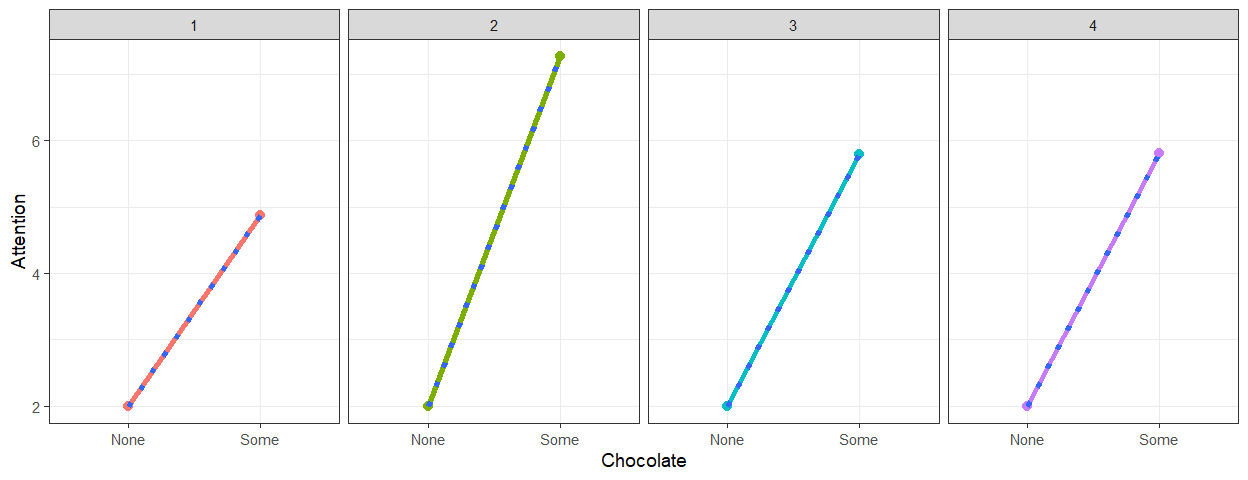
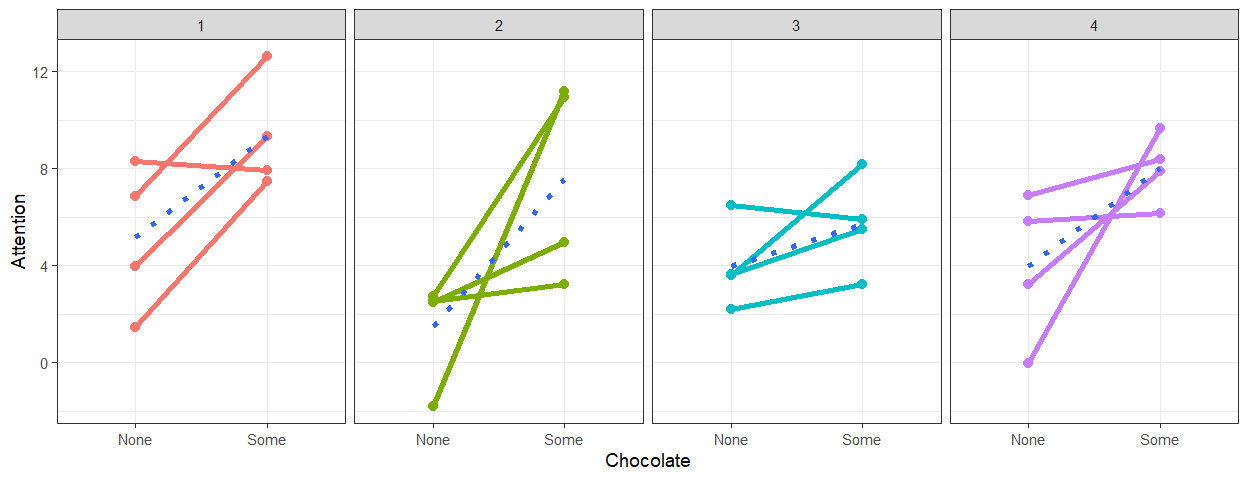
Simulation 2d: Slope Variance

• We will set \(n\) = 4, Trials=4, \(r\) = NA, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 0, \(\sigma^2_{M2}\) = 4, \(\sigma^2_{measurement}\) = 0

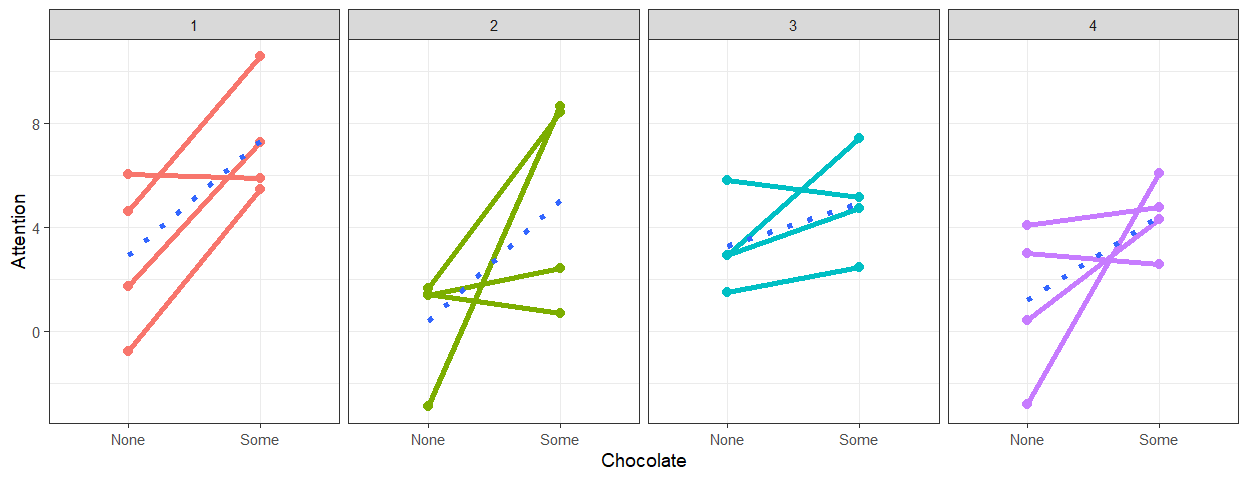
Simulation 2e: Intercept + Slope Variance

• We will set \(n\) = 4, Trials=4, \(r\) = NA, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 4, \(\sigma^2_{M2}\) = 4, \(\sigma^2_{measurement}\) = 0

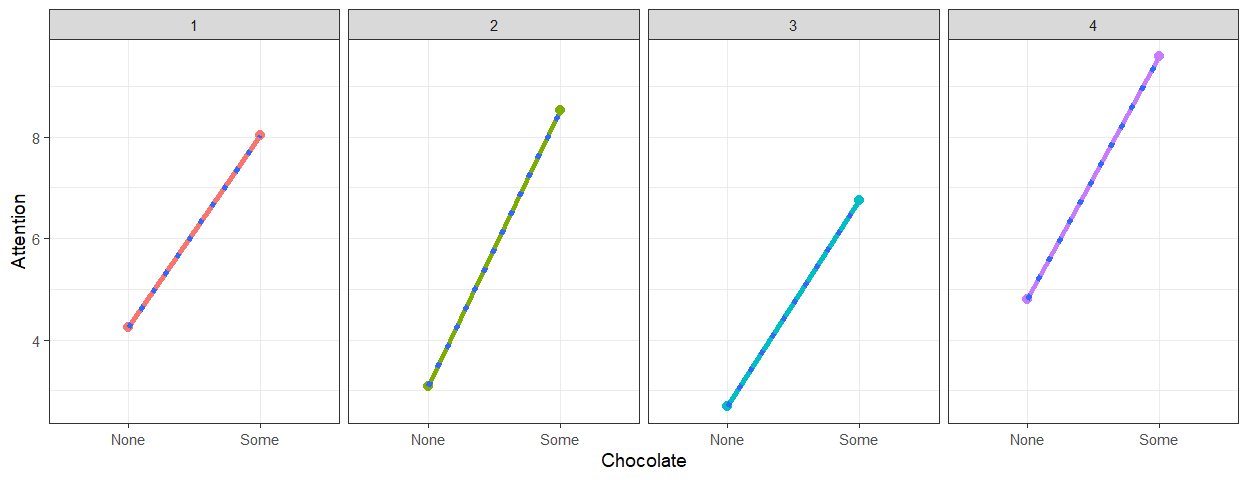
Simulation 2f: Intercept + Slope Variance + Measurement Noise

• We will set \(n\) = 4, Trials=4, \(r\) = .6, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 4, \(\sigma^2_{M2}\) = 4, \(\sigma^2_{measurement}\) = 4

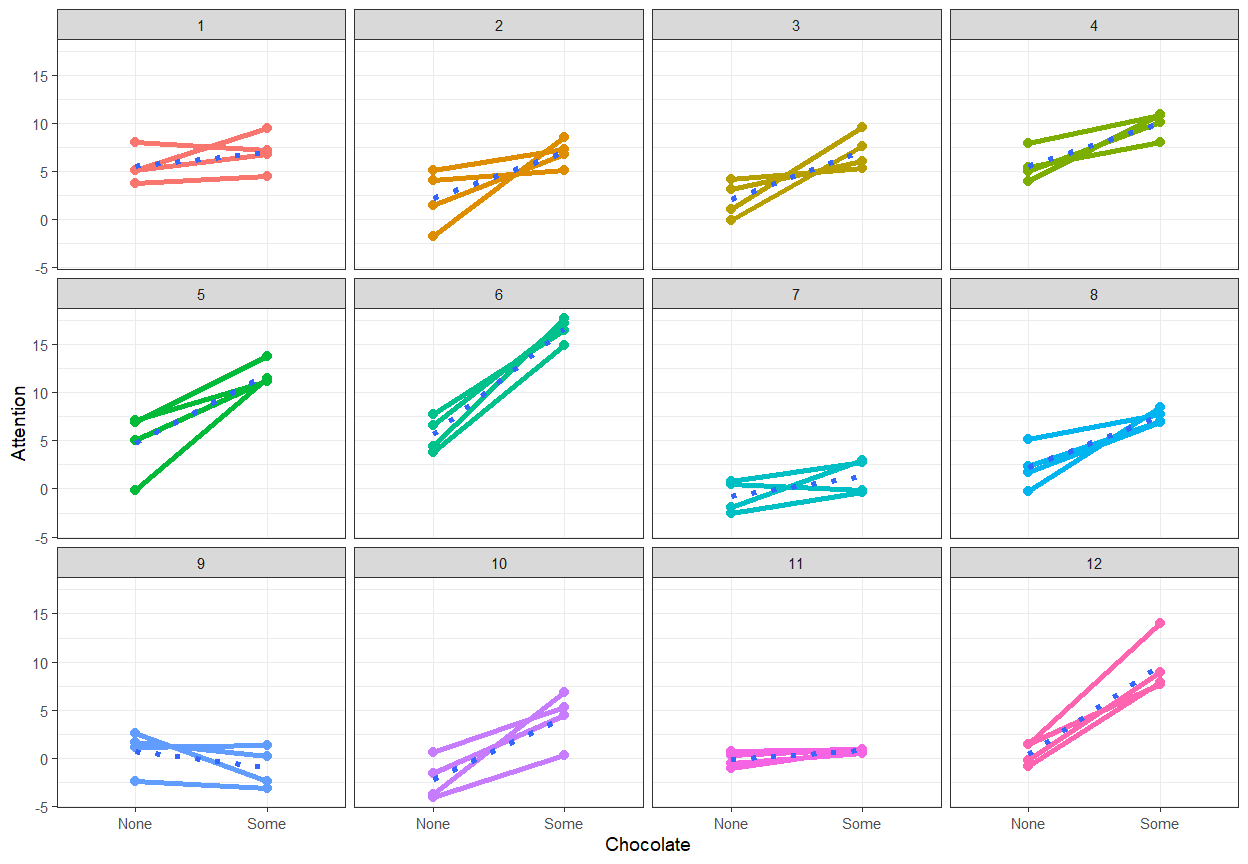
Simulation 2g: Fitting Mixed Model

• We will set \(n\) = 12, Trials=4, \(r\) = .6, \(M_1\) = 2 and \(M_2\) = 4, \(\sigma^2_{M1}\) = 4, \(\sigma^2_{M2}\) = 4, \(\sigma^2_{measurement}\) = 4

• Spaghetti plot

Test Random Intercepts & Slopes

• Model 2a: Random intercepts
• Model 2b: Random intercepts & Slopes (correlated)

Model.2a<-lmer(Attention~Chocolate
               +(1|SS),
               data=DataSim2g, REML=FALSE)

Model.2b<-lmer(Attention~Chocolate
               +(1+Chocolate|SS),
               data=DataSim2g, REML=FALSE)

<!DOCTYPE html>

	Model 1	Model 2
(Intercept)	2.17 (1.03)*	2.17 (0.75)**
ChocolateSome	4.67 (0.53)***	4.67 (0.99)***
AIC	494.75	467.40
BIC	505.01	482.78
Log Likelihood	-243.38	-227.70
Num. obs.	96	96
Num. groups: SS	12	12
Var: SS (Intercept)	11.03	5.75
Var: Residual	6.69	3.90
Var: SS ChocolateSome		9.76
Cov: SS (Intercept) ChocolateSome		3.19
***p < 0.001; **p < 0.01; *p < 0.05

Test Random Slope

• Just as we did in MLM, we will test to see if the random slope improves the fit, anova(Model.2a,Model.2b)

	npar	AIC	BIC	logLik	deviance	Chisq	Df	Pr(>Chisq)
Model.2a	4	494.7545	505.0119	-243.3772	486.7545	NA	NA	NA
Model.2b	6	467.3984	482.7845	-227.6992	455.3984	31.35608	2	2e-07

Plot Predicted Results

DataSim2g$FRa<-predict(Model.2a)  #Fixed + random
DataSim2g$FRb<-predict(Model.2b)  #Fixed + random

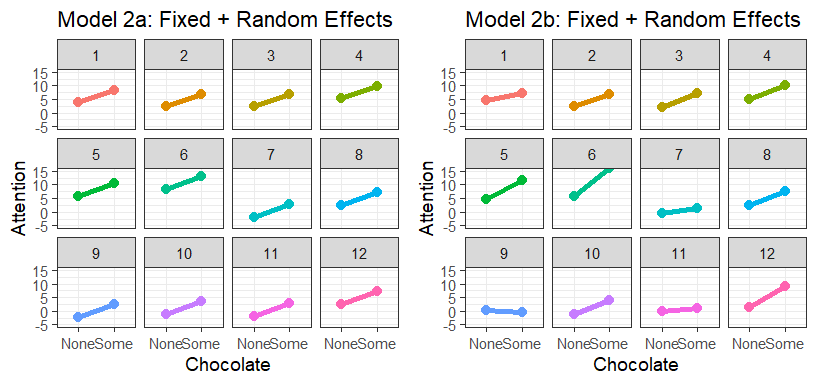
Notes

• Watch the correlation between them random slopes and intercept carefully (make sure they are not correlated at 1)
• The more trials, the better and the more stable from measurement to measurement the better
• The stronger the correlation between experimental condition the higher your power will be

2 Factors: 2 X 3 Level Designs

• Not only do we have to deal with all the parameters we had before, but we would also have understood the correlations within subjects across factors
• The question for today is how to deal with a factor that has 3 levels
  • Examine this I heavily manipulated data from my paper (Demos & Chaffin, in press)
• Listeners were asked to listen (and move their bodies) relative to recorded solo trombone music played by 2 different performers at 3 levels of expression. As part of the study, they were asked to report how expressive they though the music was. Note: I have simplified the design and edited the data: thus, results will not match the paper.
  • We will assume a fully crossed design where every subject heard each performer play at each expressive level, 2 times. \(n\) = 16, Ratings were 1-6 on expression.
• Read in the data:

MP.Data<-read.csv("Mixed/MusicPerception.csv")
MP.Data$Perf<-factor(MP.Data$Performer,
                          levels=c(0,1),
                          labels=c("M1","M2"))
MP.Data$Level<-factor(MP.Data$Condition,
                     levels=c(0,1,2),
                     labels=c("Normal","Exp","Non-Exp"))
MP.Data$SS<-as.factor(MP.Data$SS)

Plot Study

• This is categorical data, so can do box plots/violin plots [helpful for when we want to see the variance]

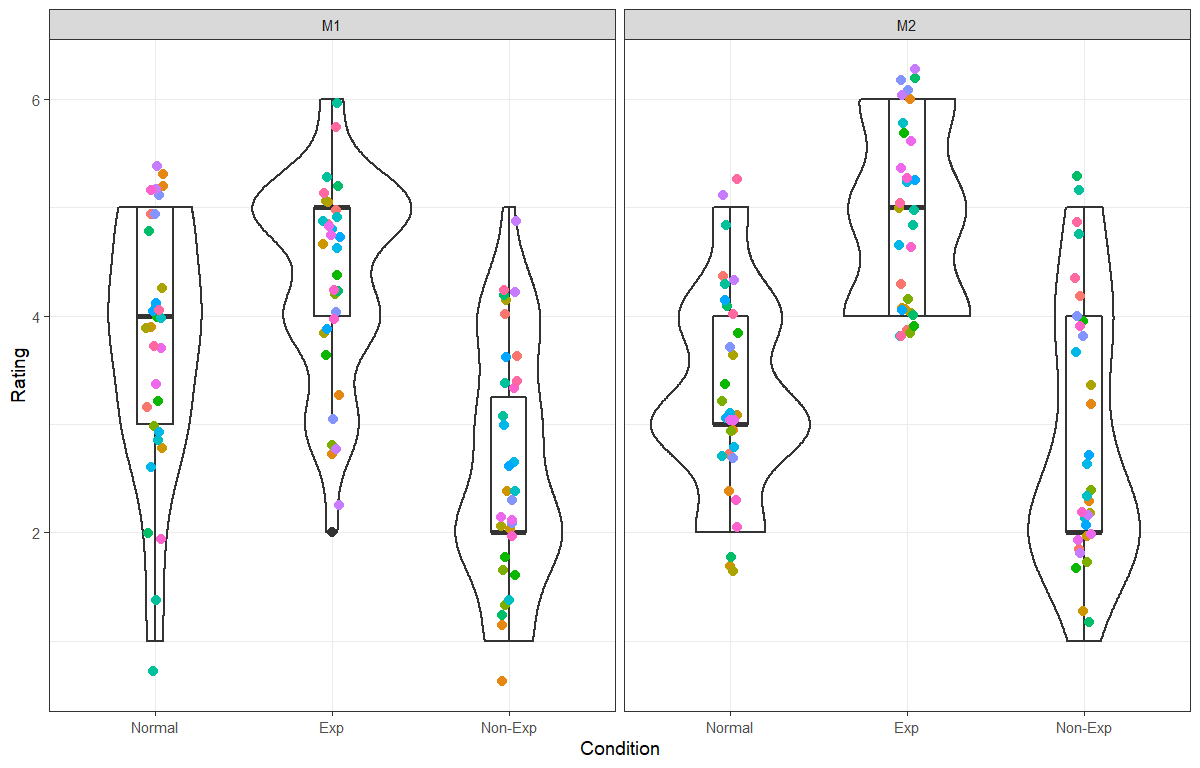
• We can also try to our spaghetti plots in different ways

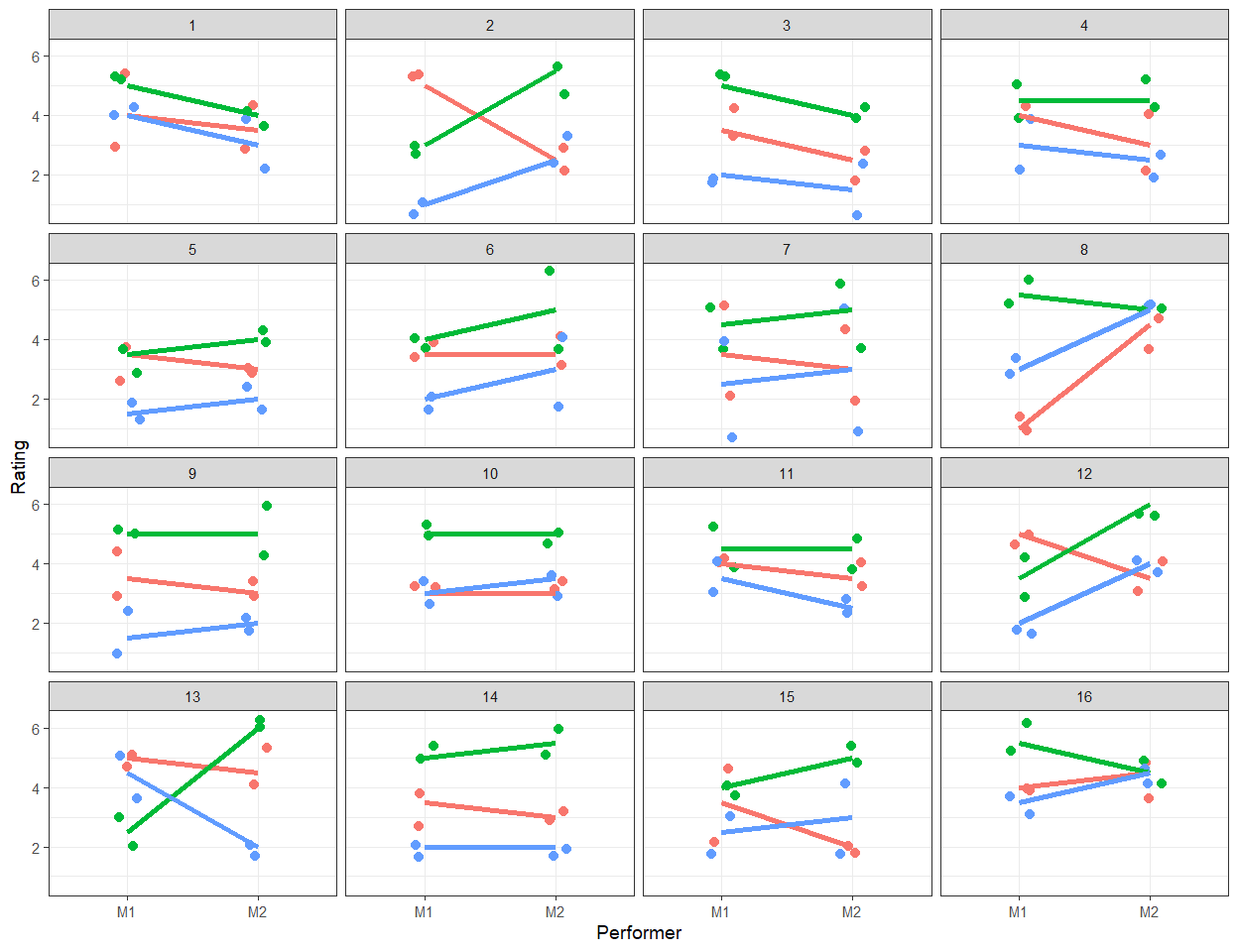
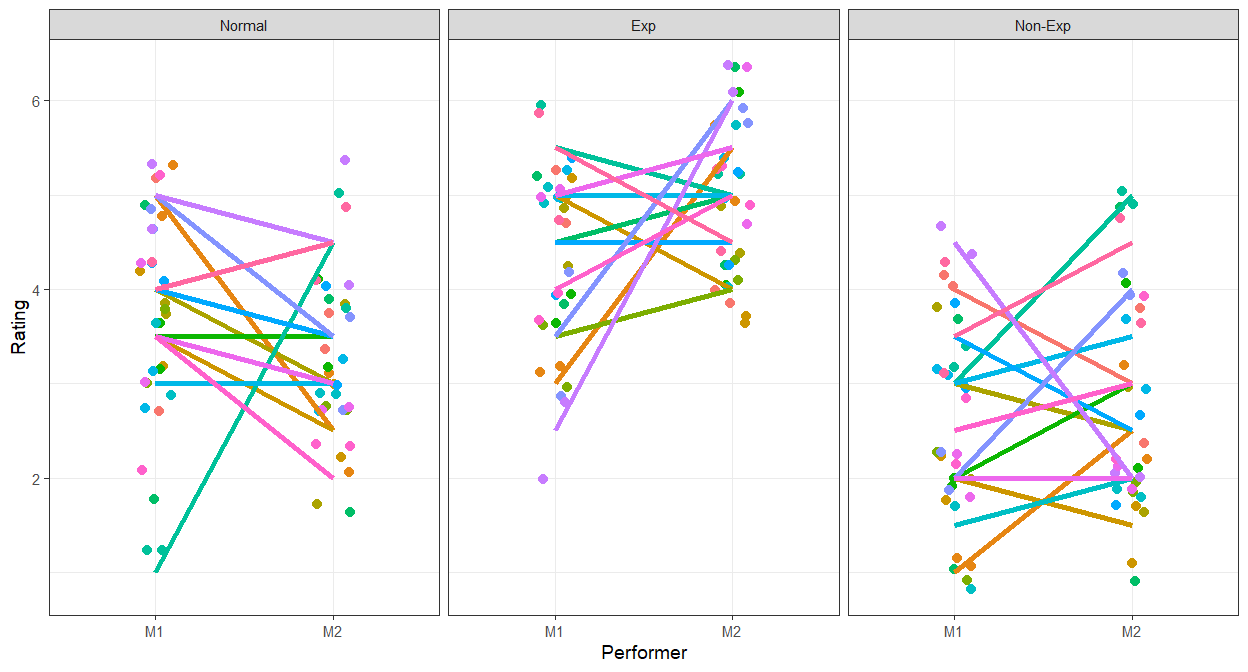
Random Categorical Factor

• Let’s treat the data as categorical
• We will examine Level as a fixed and random effects only First

M0<-lmer(Rating~ Level+ (1|SS), data=MP.Data, REML=TRUE)
M1<-lmer(Rating~ Level+ (1+Level|SS), data=MP.Data, REML=TRUE)
summary(M1, correlation=FALSE)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Rating ~ Level + (1 + Level | SS)
##    Data: MP.Data
## 
## REML criterion at convergence: 554.2
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.69937 -0.64286 -0.01363  0.54687  2.36725 
## 
## Random effects:
##  Groups   Name         Variance Std.Dev. Corr       
##  SS       (Intercept)  0.1043   0.3229              
##           LevelExp     0.1559   0.3949   -0.90      
##           LevelNon-Exp 0.2758   0.5251   -0.01  0.45
##  Residual              0.9235   0.9610              
## Number of obs: 192, groups:  SS, 16
## 
## Fixed effects:
##              Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)    3.5000     0.1447 16.6830  24.182 2.01e-14 ***
## LevelExp       1.1406     0.1965 16.9206   5.805 2.15e-05 ***
## LevelNon-Exp  -0.7656     0.2147 17.1144  -3.566  0.00236 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Let’s examine the random effects in more detail:

Rm1<-ranef(M1)

(Intercept)	LevelExp	LevelNon-Exp
0.1783985	-0.1029686	0.2792666
-0.0360456	-0.1430073	-0.5537304
-0.2549083	0.1466367	-0.4005292
0.0118790	-0.0201604	-0.0217933
-0.1354541	-0.0456614	-0.5880064
-0.0212470	-0.0207507	-0.1334851

• The random intercept now represents random effect at Level = Normal for each subject and the differences for the other conditions

Plot Predicted Results

MP.Data$FRa<-predict(M0)  #Fixed + random
MP.Data$FRb<-predict(M1)  #Fixed + random

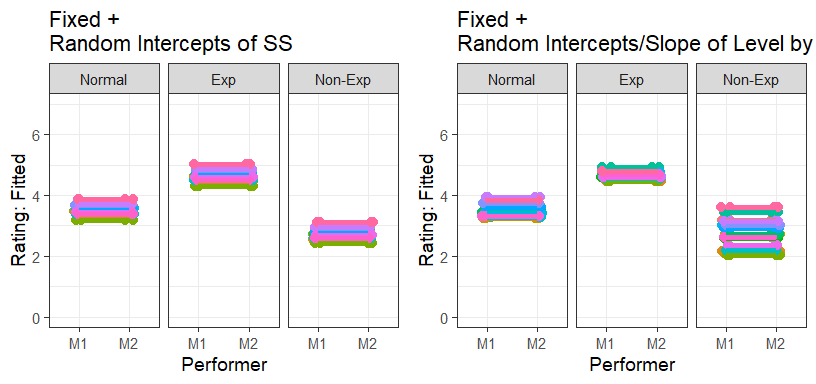
• This captured the differences between Levels, but we still have to work on the other factor to deal with
• Let’s add fixed and random effect of Performer

2 Random Categorical Factors

M2<-lmer(Rating~ Level+Perf+ (1+Level|SS), data=MP.Data, REML=TRUE)
M3<-lmer(Rating~ Level+Perf+ (1+Level+Perf|SS), data=MP.Data, REML=TRUE)
summary(M3, correlation=FALSE)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Rating ~ Level + Perf + (1 + Level + Perf | SS)
##    Data: MP.Data
## 
## REML criterion at convergence: 553.1
## 
## Scaled residuals: 
##      Min       1Q   Median       3Q      Max 
## -2.70103 -0.60603 -0.06199  0.52791  2.32239 
## 
## Random effects:
##  Groups   Name         Variance Std.Dev. Corr             
##  SS       (Intercept)  0.1552   0.3939                    
##           LevelExp     0.1759   0.4195   -0.98            
##           LevelNon-Exp 0.2814   0.5304   -0.39  0.47      
##           PerfM2       0.1227   0.3503   -0.55  0.51  0.82
##  Residual              0.8894   0.9431                    
## Number of obs: 192, groups:  SS, 16
## 
## Fixed effects:
##              Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)    3.4375     0.1680 16.3744  20.461 4.31e-13 ***
## LevelExp       1.1406     0.1970 16.9756   5.791 2.18e-05 ***
## LevelNon-Exp  -0.7656     0.2130 16.7482  -3.594  0.00228 ** 
## PerfM2         0.1250     0.1619 15.1948   0.772  0.45178    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Let’s examine the random effects in more detail (shortened version):

R.M3<-ranef(M3)

(Intercept)	LevelExp	LevelNon-Exp	PerfM2
0.3110008	-0.2768702	0.0644461	-0.1089660
0.0061816	-0.0635005	-0.4362016	-0.1603991
-0.0384346	0.0356336	-0.5536842	-0.3538819
0.1269346	-0.1172792	-0.1440845	-0.1483003
-0.0295522	-0.0151833	-0.5375279	-0.2485711
-0.0887203	0.0674438	-0.0170347	0.0585761

Plot Predicted Results

MP.Data$FRc<-predict(M2)  #Fixed + random
MP.Data$FRd<-predict(M3)  #Fixed + random

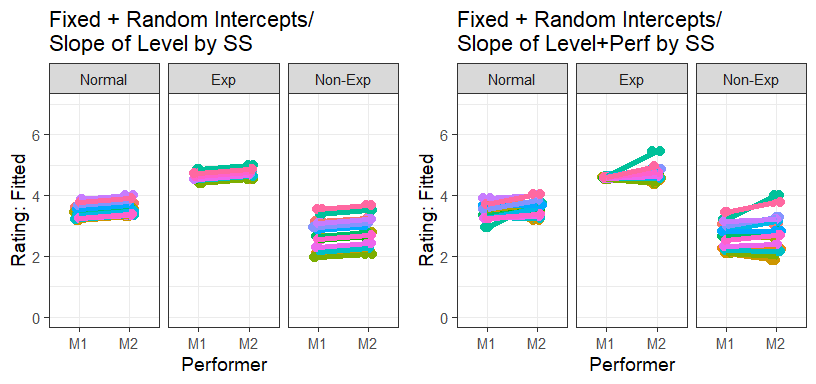
• This captured the differences between Levels and Performer, but is it possible that they interact?
• Let’s add fixed and random effect of interaction

2 Random Categorical Factors Interacted

M4<-lmer(Rating~ Level*Perf+ (1+Level+Perf|SS), data=MP.Data, REML=TRUE)
M5<-lmer(Rating~ Level*Perf+ (1+Level*Perf|SS), data=MP.Data, REML=TRUE)
summary(M5)

## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Rating ~ Level * Perf + (1 + Level * Perf | SS)
##    Data: MP.Data
## 
## REML criterion at convergence: 509.2
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.5652 -0.6345  0.1111  0.5689  2.7334 
## 
## Random effects:
##  Groups   Name                Variance Std.Dev. Corr                         
##  SS       (Intercept)         0.6194   0.7870                                
##           LevelExp            2.2437   1.4979   -0.99                        
##           LevelNon-Exp        1.2875   1.1347   -0.69  0.75                  
##           PerfM2              1.0747   1.0367   -0.84  0.85  0.92            
##           LevelExp:PerfM2     3.7986   1.9490    0.93 -0.97 -0.88 -0.91      
##           LevelNon-Exp:PerfM2 1.2807   1.1317    0.36 -0.46 -0.89 -0.64  0.66
##  Residual                     0.5699   0.7549                                
## Number of obs: 192, groups:  SS, 16
## 
## Fixed effects:
##                     Estimate Std. Error      df t value Pr(>|t|)    
## (Intercept)           3.7187     0.2377 15.0942  15.642 9.78e-11 ***
## LevelExp              0.6563     0.4193 15.0473   1.565  0.13838    
## LevelNon-Exp         -1.1250     0.3407 15.3179  -3.302  0.00473 ** 
## PerfM2               -0.4375     0.3206 15.5291  -1.365  0.19183    
## LevelExp:PerfM2       0.9687     0.5556 15.1891   1.744  0.10140    
## LevelNon-Exp:PerfM2   0.7187     0.3889 15.2653   1.848  0.08408 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) LvlExp LvlN-E PerfM2 LE:PM2
## LevelExp    -0.908                            
## LevelNn-Exp -0.695  0.679                     
## PerfM2      -0.797  0.743  0.783              
## LvlExp:PrM2  0.810 -0.911 -0.740 -0.845       
## LvlNn-E:PM2  0.410 -0.406 -0.806 -0.664  0.583
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')

• Let’s examine the random effects in more detail (shortened version):

R.M5<-ranef(M5)

(Intercept)	LevelExp	LevelNon-Exp	PerfM2	LevelExp:PerfM2	LevelNon-Exp:PerfM2
-0.0925771	0.4910901	1.0818923	0.4822347	-1.2236641	-1.4530276
0.9465210	-2.0637509	-2.0927606	-1.5701238	3.2370158	2.0782845
-0.2187872	0.5661589	-0.3028806	-0.4769871	-0.4368355	0.0360365
0.1202466	-0.0866788	0.0818598	-0.1796201	-0.0362446	-0.3646549
0.1335468	-0.3095779	-0.8671259	-0.7380190	0.8022893	0.7472702
-0.0273855	-0.0785710	-0.2937242	-0.0511187	0.3036436	0.4865756

Plot Predicted Results

MP.Data$FRe<-predict(M4)  #Fixed + random
MP.Data$FRf<-predict(M5)  #Fixed + random

• Check fit

	npar	AIC	BIC	logLik	deviance	Chisq	Df	Pr(>Chisq)
M0	5	564.8267	581.1142	-277.4134	554.8267	NA	NA	NA
M1	10	568.3399	600.9149	-274.1700	548.3399	6.4867941	5	0.2616889
M2	11	569.5206	605.3531	-273.7603	547.5206	0.8192972	1	0.3653857
M3	15	575.2012	624.0636	-272.6006	545.2012	2.3194254	4	0.6772346
M4	17	569.7327	625.1101	-267.8664	535.7327	9.4685068	2	0.0087890
M5	28	556.2594	647.4693	-250.1297	500.2594	35.4733040	11	0.0002070

• The models seem to support the conclusion that we should fully cross the random effects and account for the random variance on both their main effects and interactions, what Barr et al. 2013 call a maximal random structure
• We will come back to this concept next week and talk in more details about the process of fitting complex random structures
• We will also talk about how to do post-hoc testing

Notes:

• Note: The final model was 28 degrees of freedom, and I only had 16 subjects (but I had 192 observations)
  • This a highly parameterized model given the small amount of data I had.
    • The final model had 15 random correlations between terms.
  • You will rarely get a fit with such a complex model with such little data