Main-Effects
\(H_0\): All groups have equal means
\(H_1\): At least 1 group is different from the other
Calculating the Two-Way ANOVA
Design Example
Kardas & O’Brien (2018) recently reported that with the proliferation of YouTube videos, people seem to think they can learn by seeing rather than doing. They “hypothesized that the more people merely watch others, the more they believe they can perform the skill themselves.” They compared extensively watching the “tablecloth trick with extensively reading or thinking about it. Participants assessed their own abilities to perform the”tablecloth trick.” Participants were asked to rate from 1 (I feel there’s no chance at all I’d succeed on this attempt) to 7 (I feel I’d definitely succeed without a doubt on this attempt). The study was a 3 (type of exposure: watch, read, think) X 2 (amount of exposure: low, high) between-subjects design. They collected an N = 1,003 with small effect sizes (\(n^2 <.06\)), but to make this analysis doable by hand I will cut the same to 5 people per cell and inflate the effect size (but keep the pattern the same as their experiment 1).
| Low Exposure Group | Watching | Reading | Thinking | Row Means |
|---|---|---|---|---|
| \(\,\) | 1 | 3 | 3 | |
| \(\,\) | 3 | 2 | 3 | |
| \(\,\) | 3 | 3 | 2 | |
| \(\,\) | 4 | 1 | 3 | |
| \(\,\) | 2 | 4 | 1 | |
| ———————— | ——— | ———- | ———- | ———- |
| Cell Means | 2.6 | 2.6 | 2.4 | 2.53 |
| Cell SS | 5.2 | 5.2 | 3.2 |
| High Exposure Group | Watching | Reading | Thinking | Row Means |
|---|---|---|---|---|
| \(\,\) | 6 | 5 | 3 | |
| \(\,\) | 4 | 3 | 2 | |
| \(\,\) | 7 | 2 | 1 | |
| \(\,\) | 5 | 3 | 4 | |
| \(\,\) | 5 | 2 | 4 | |
| ———————— | ——— | ———- | ———- | ———- |
| Cell Means | 5.4 | 3.0 | 2.8 | 3.73 |
| Cell SS | 5.2 | 6.0 | 6.8 | |
| Column Means | 4.0 | 2.8 | 2.6 | G = 3.13 |
Logic of Two-Way ANOVA
We now have two factors, and we will test the main effects and interaction.
- Main effect (Factor A: Rows): The independent effects of Length of Exposure on Perceived Ability
- Main effect (Factor B: Columns): The independent effects of Type of Exposure on Perceived Ability
- Interaction: The joint effects of Length and Type of Exposure on Perceived Ability
Hypotheses
Interaction
\(H_0\): There is no interaction between factors A and B. All the mean differences between treatment conditions are explained by the main effects.
\(H_1\): There is an interaction between factors A and B. The mean differences between treatment conditions are not what would be predicted from the overall main effects of the two factors.
Logic Variance Parsing
One-way ANOVA has Only one factor to test: \(SS_T = SS_{W}+SS_{B}\)
Two-way ANOVA has multiple factors to test: \(SS_T = SS_{W}+ (SS_{FactorA}+SS_{FactorB}+SS_{AxB})\)
Note that in the two-way ANOVA: \(SS_B = (SS_{FactorA}+SS_{FactorB}+SS_{AxB})\)
F-Ratio Logic
Omnibus F (same as one-way)
\[F= \frac{MS_{B}}{MS_{W}}\]
This will still tell is if one cell is different from another, but we also have to calculate F-tests on Factors A, B, and the AxB
\[F= \frac{MS_{FactorA}}{MS_{W}}\] \[F= \frac{MS_{FactorB}}{MS_{W}}\] \[F= \frac{MS_{AXB}}{MS_{W}}\]
Analysis Procedures
One-way ANOVA Review (simplified for equal sample sizes)
With the formulas (formal equations)
| Source | SS | DF | MS | F |
|---|---|---|---|---|
| Between | \(n\displaystyle\sum_{i=1}^{k}(M_i-G)^2\) | \(K-1\) | \(\frac{SS_B}{df_B}\) | \(\frac{MS_B}{MS_W}\) |
| Within | \(\displaystyle \sum_{i=1}^{K}\sum_{j=1}^{n}(X_{i_{j}}-M_i)^2\) | \(N-K\) | \(\frac{SS_W}{df_W}\) | |
| Total | \(\displaystyle\sum_{j=1}^{N}(X_j-G)^2\) | \(N-1\) |
With the formulas (conceptually simplified)
| Source | SS | DF | MS | F |
|---|---|---|---|---|
| Between | \(nSS_{treatment}\) | \(K-1\) | \(\frac{SS_B}{df_B}\) | \(\frac{MS_B}{MS_W}\) |
| Within | \(\displaystyle \sum SS_{within}\) | \(N-K\) | \(\frac{SS_W}{df_W}\) | |
| Total | \(SS_{scores}\) | \(N-1\) |
Note: \(SS_B + SS_W = SS_T\) & \(df_B + df_W = df_T\)
Two-way ANOVA Review (simplified for equal sample sizes)
| Source | SS | DF | MS | F |
|---|---|---|---|---|
| Between | \(SS_B\) | \(df_B\) | \(MS_B\) | F |
| \(Factor\,A_{Row}\) | \(SS_r\) | \(df_r\) | \(MS_r\) | F |
| \(Factor\,B_{Col}\) | \(SS_c\) | \(df_c\) | \(MS_c\) | F |
| \(Factor\,AxB\) | \(SS_{rxc}\) | \(df_{rxc}\) | \(MS_{rxc}\) | F |
| Within | \(SS_W\) | \(df_W\) | \(MS_W\) | |
| Total | \(SS_T\) | \(df_T\) |
With the formulas (formal equations)
| Source | SS | DF | MS | F |
|---|---|---|---|---|
| Between | \(\tiny n\displaystyle\biggl(\sum_{w=1}^{r}(M_r-G)^2+\sum_{u=1}^{c}(M_c-G)^2\biggr)\) | \(rc-1\) | \(\frac{SS_B}{df_B}\) | \(\frac{MS_B}{MS_W}\) |
| \(\,A_{(Rows)}\) | \(\tiny n_r\displaystyle\sum_{w=1}^{r}(M_w-G)^2\) | \(r-1\) | \(\frac{SS_r}{df_r}\) | \(\frac{MS_r}{MS_W}\) |
| \(\,B_{(Col)}\) | \(\tiny n_c\displaystyle\sum_{u=1}^{c}(M_u-G)^2\) | \(c-1\) | \(\frac{SS_c}{df_c}\) | \(\frac{MS_c}{MS_W}\) |
| \(\,AxB\) | \(\tiny SS_{B}-(SS_r-SS_c)\) | \((r-1)(c-1)\) | \(\frac{SS_{rxc}}{df_{rxc}}\) | \(\frac{MS_{rxc}}{MS_W}\) |
| Within | \(\tiny \displaystyle \sum_{w=1}^{r}\sum_{j=1}^{n}(X_{w_{j}}-M_w)^2+\displaystyle \sum_{u=1}^{c}\sum_{j=1}^{n}(X_{u_{j}}-M_u)^2\) | \(nrc-rc\) | \(\frac{SS_w}{df_w}\) | |
| Total | \(\tiny \displaystyle\sum_{j=1}^{N}(X_j-G)^2\) | \(nrc-1\) |
With the formulas (conceptually simplified)
| Source | SS | DF | MS | F |
|---|---|---|---|---|
| Between | \(nSS_{all\,cell\,means}\) | \(rc-1\) | \(\frac{SS_B}{df_B}\) | \(\frac{MS_B}{MS_W}\) |
| \(\,A_{(Rows)}\) | \(n_rSS_{row\,means}\) | \(r-1\) | \(\frac{SS_r}{df_r}\) | \(\frac{MS_r}{MS_W}\) |
| \(\,B_{(Cols)}\) | \(n_cSS_{col\,means}\) | \(c-1\) | \(\frac{SS_c}{df_c}\) | \(\frac{MS_c}{MS_W}\) |
| \(\,AxB\) | \(\tiny SS_{B}-(SS_r-SS_c)\) | \((r-1)(c-1)\) | \(\frac{SS_{rxc}}{df_{rxc}}\) | \(\frac{MS_{rxc}}{MS_W}\) |
| Within | \(\displaystyle \sum SS_{within}\) | \(nrc-rc\) | \(\frac{SS_w}{df_w}\) | |
| Total | \(SS_{scores}\) | \(nrc-1\) |
Note for SS: \(SS_B + SS_W = SS_T\) & \(SS_B = SS_r + SS_c+ SS_{rxc}\)
Note for DF: \(df_B + df_W = df_T\) & \(df_B = df_r + df_c+ df_{rxc}\)
Effect size
Eta-Squared
Just like one-way ANOVA, we will use eta-squared = proportion of variance the treatment accounts for. Remember \(SS_B\) is the variation caused by treatment, and \(SS_T\) is the variation of Treatment + Noise.
\[\eta_B^2 = \frac{SS_B}{SS_B+SS_W} = \frac{SS_B}{SS_T}\]
\[\eta_r^2 = \frac{SS_r}{SS_T}\]
\[\eta_c^2 = \frac{SS_c}{SS_T}\]
\[\eta_{rxc}^2 = \frac{SS_{rxc}}{SS_T}\]
Partial Eta-Squared
Eta-squared the = proportion of the total (variance) pie this effect is accounting for. The nice thing is that eta-squared adds can be used to add up to 100%! However, the values calculated thus depend upon the number of other effects and the magnitude of those other effects.
People often prefer to report Partial Eta-Squared, \(\eta_p^2\) = ratio: effect / error variance that is attributable to the effect. This “controls” for the other effects and reports what the effect is relative to the noise (not total). This is “ratio” where eta-squared was a “proportion”. Thus you cannot sum them up to 100%.
\[\eta_{p_{r}}^2 = \frac{SS_r}{SS_T-(SS_c-SS_{rxc})}\]
\[\eta_{p_{c}}^2 = \frac{SS_c}{SS_T-(SS_r-SS_{rxc})}\]
\[\eta_{p_{rxc}}^2 = \frac{SS_{rxc}}{SS_T-(SS_r-SS_c)}\]
This Partial Eta-Squared formula for two-way ANOVA is equal to the more modern generalized-eta squared \(\eta^2_g\) that R automatically generates (in the case that between subject treatment conditions were manipulated). When they are not-manipulated (like gender) that formulas change a bit which we will talk about next week along with \(\omega^2_g\) for bias correction.
Analysis in R
Build our data frame (or read in csv)
I build our data frame by hand in the long format.
n=5; r=2; c=3;
Example.Data<-data.frame(ID=seq(1:(n*r*c)),
Level=c(rep("Low",(n*c)),rep("High",(n*c))),
Type=rep(c(rep("Watching",n),rep("Reading",n),rep("Thinking",n)),2),
Percieved.Ability = c(1,3,3,4,2,3,2,3,1,4,3,3,2,3,1,
6,4,7,5,5,5,3,2,3,2,3,2,1,4,4))
# Also, I want to re-set the order using the `factor` command and set the order I want.
Example.Data$Level<-factor(Example.Data$Level,
levels = c("Low","High"),
labels = c("Low","High"))
Example.Data$Type<-factor(Example.Data$Type,
levels = c("Watching","Reading","Thinking"),
labels = c("Watching","Reading","Thinking"))Check the means and SS calculations with dpylr
library(dplyr)
Means.Table<-Example.Data %>%
group_by(Level,Type) %>%
summarise(N=n(),
Means=mean(Percieved.Ability),
SS=sum((Percieved.Ability-Means)^2),
SD=sd(Percieved.Ability),
SEM=SD/N^.5)
knitr::kable(Means.Table, digits = 2)
# Note remember knitr::kable makes it pretty, but you can just call `Means.Table`| Level | Type | N | Means | SS | SD | SEM |
|---|---|---|---|---|---|---|
| Low | Watching | 5 | 2.6 | 5.2 | 1.14 | 0.51 |
| Low | Reading | 5 | 2.6 | 5.2 | 1.14 | 0.51 |
| Low | Thinking | 5 | 2.4 | 3.2 | 0.89 | 0.40 |
| High | Watching | 5 | 5.4 | 5.2 | 1.14 | 0.51 |
| High | Reading | 5 | 3.0 | 6.0 | 1.22 | 0.55 |
| High | Thinking | 5 | 2.8 | 6.8 | 1.30 | 0.58 |
Plot Study
Normally we plot bar graphs with 1 SEM unit. I used the object I
created Means.Table that has the means. A We will apply
some fancy code to make our plot more APA!
library(ggplot2)
Plot.1<-ggplot(Means.Table, aes(x = Type, y = Means, group=Level))+
geom_col(aes(group=Level, fill=Level), position=position_dodge(width=0.9))+
scale_y_continuous(expand = c(0, 0))+ # Forces plot to start at zero
geom_errorbar(aes(ymax = Means + SEM, ymin= Means - SEM),
position=position_dodge(width=0.9), width=0.25)+
scale_fill_manual(values=c("#f44141","#4286f4"))+
xlab('')+
ylab('Percieved Ability')+
theme_bw()+
theme(panel.grid.major=element_blank(),
panel.grid.minor=element_blank(),
panel.border=element_blank(),
axis.line=element_line(),
legend.title=element_blank())
Plot.1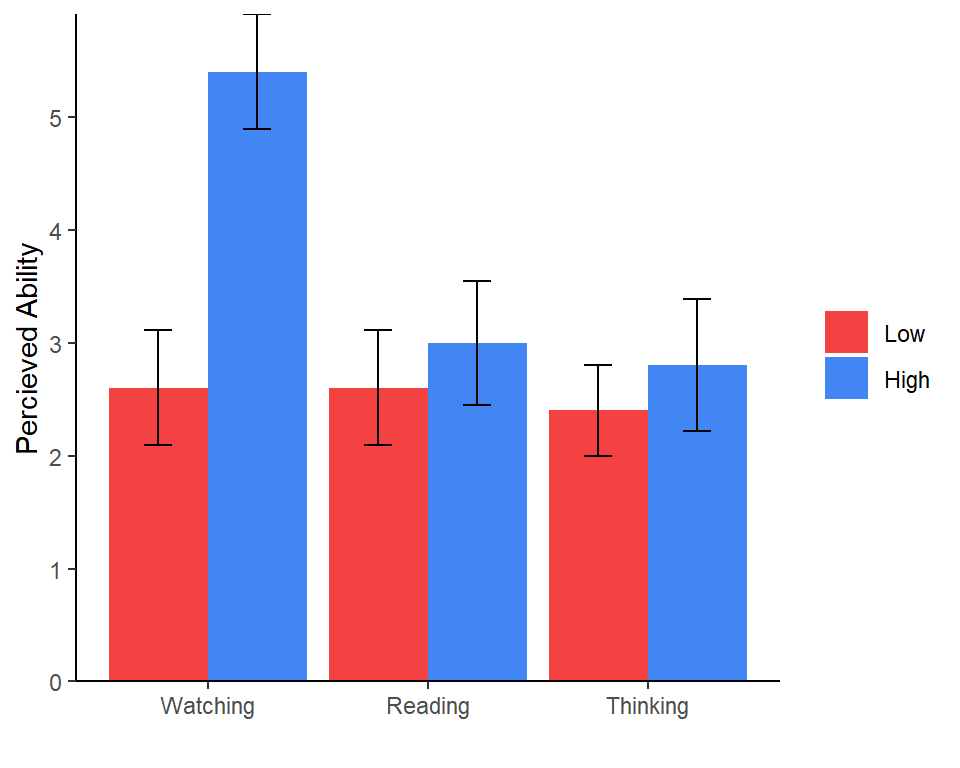
Which effects do you predict will be significant?
Run ANOVA
Again, we will use the afex package developed to allow
people to do SPSS-like ANOVA in R (Type III).
ANOVA style output
- This style is close to our ANOVA source table, but instead its formatted like a regression F-source table.
- You can ignore the intercept line (we will cover that next semester).
- Level = \(SS_r\): Main effect of Level of Exposure (note R will give the order you called them. I put rows first in the formula below).
- Type = \(SS_c\): Main effect of Type of Exposure
- Level:Type = \(SS_{rxc}\): Interaction between Level and Type of Exposure
- Residual = \(SS_{w}\): Residual in regression means leftover (and this it the error term: chance)
- There is no total (you can do that with addition)
library(afex)
ANOVA.JA.Table<-aov_car(Percieved.Ability~Level*Type + Error(ID),
data=Example.Data, return='Anova')
ANOVA.JA.Table| Sum Sq | Df | F value | Pr(>F) | |
|---|---|---|---|---|
| (Intercept) | 294.53333 | 1 | 223.696202 | 0.0000000 |
| Level | 10.80000 | 1 | 8.202532 | 0.0085526 |
| Type | 11.46667 | 2 | 4.354430 | 0.0243529 |
| Level:Type | 9.60000 | 2 | 3.645570 | 0.0414456 |
| Residuals | 31.60000 | 24 | NA | NA |
Nice style output
- This style reports everything you need to report in APA format (just
leave the return argument off or write
nice)
library(afex)
Nice.JA.Table<-aov_car(Percieved.Ability~Level*Type + Error(ID),
data=Example.Data)
Nice.JA.Table## Anova Table (Type 3 tests)
##
## Response: Percieved.Ability
## Effect df MSE F ges p.value
## 1 Level 1, 24 1.32 8.20 ** .255 .009
## 2 Type 2, 24 1.32 4.35 * .266 .024
## 3 Level:Type 2, 24 1.32 3.65 * .233 .041
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1Understanding \(\eta^2\)
\(\eta^2\) is a useful method for understanding how your ANOVA “parsed” your variance, but not always as useful to report in papers
Here we see that Type, Level, and Type X Level are “Explained Variance”. In total, you explained about 50% of the variance. The error term is “Unexplained Variance” (the residual). It is important you do not confuse \(\eta^2\) (the chart below) with \(\eta_p^2\).
Assumptions
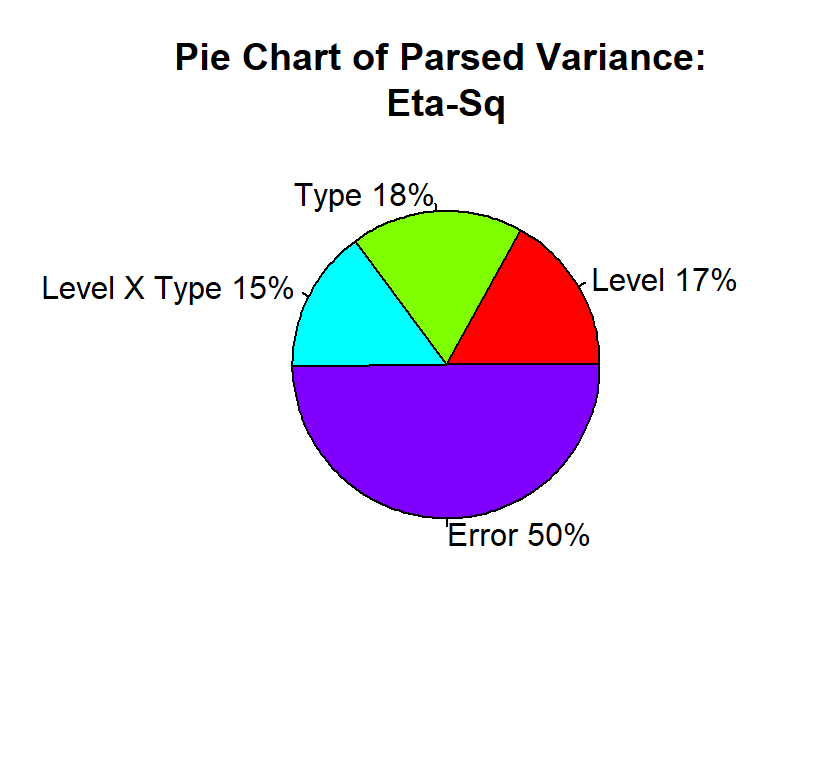
We assume HOV and normality. We can test for HOV using Levene’s test formula, which is like the Brown-Forsythe test we used for one-way ANOVA, but we can apply it multiple factors.
Using the car package, we can test our violations. Just
like Brown-Forsythe, you do NOT want this test to be significant.
library(car)
leveneTest(Percieved.Ability ~ Level*Type, data = Example.Data) | Df | F value | Pr(>F) | |
|---|---|---|---|
| group | 5 | 0.1170732 | 0.9873727 |
| 24 | NA | NA |
Often we examine QQ plots of the DV. If the data points are very different from the line, it suggests violations of normality.
qqnorm(Example.Data$Percieved.Ability)
qqline(Example.Data$Percieved.Ability)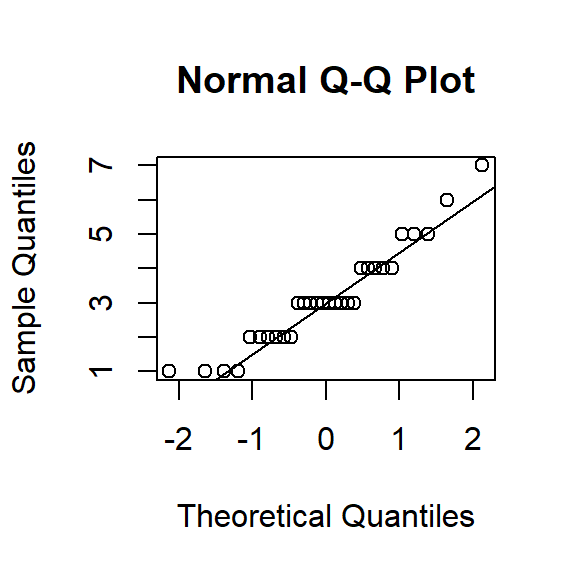
Shapiro-Wilk test is a way of testing normality statistically, but this is the test is very sensitive especially in small samples. You do NOT want this test to be significant. In our case it is, but our sample is really small.
shapiro.test(Example.Data$Percieved.Ability)##
## Shapiro-Wilk normality test
##
## data: Example.Data$Percieved.Ability
## W = 0.92911, p-value = 0.04649References
Kardas, M., & O’Brien, E. (2018). Easier Seen Than Done: Merely Watching Others Perform Can Foster an Illusion of Skill Acquisition. Psychological science, 29(4), 521-536.