Generalized Linear Model

Generalized Linear Model (GLM)

• This is a whole area in regression and we could spend a full semester on this topic. Today’s goal is a crash course on the basics of the most common type of GLM used, the logistic regression
• So far you have been using a special case of the GLM, where we assume the underlying assumption is a Gaussian distribution
• Now we will expand out the examine the whole family
• When you run a GLM, you need to state “family” and the “linking” function you will use

Family and Link

• Linear regression assumes that DV = \(\mu\) and SD = \(\sigma\) and the possible range of responses is from \(-\infty,\infty\)
  • But GLM will allow us to examine categorical responses (2 or more responses), and you cannot satisfy the same requirements as linear regression (you cannot have \(-\infty,\infty\) response range)
• Some of the other distributions, like binomial (2 responses) or Poisson (multiple responses) can approximate normal when transformed
• We need to “link” the mean of DV to the linear term of the model (think transform) to make it meet our regression requirements
  
• Here are the most common families used in psychology

Family	Variance	Link
Gaussian	Gaussian	identity
binomial	binomial	logit/Probit
Poisson	Poisson	log

Linear regression on binomial DV

• Let’s simulate what happens when we analyze binomial DV as it were a plain old regression
• What is we wanted to predict who is a hipster based on specific features of their appearance and attitude.
• Simulate a model Hipster (DV: 0 = Not a Hipster, 1 = Hipster) based on the Use of Irony (IV = -3 to 3) and Ridiculousness of transportation (IV = -3 to 3)
• The goal is to predict Hipster status
  • Below is the simulation and we will run a linear regression.
  • First a raw data plot (show the predictors one a time)!

library(ggplot2)
set.seed(42)
n=30
x = runif(n,-3,3) #  Ridiculousness of transportation [-3 normal, 3 = uni-cycles]
j = runif(n,-3,3) #  Irony usage [-3 never, 3 = All the time]
z =  .8*x + .2*j         
pr = 1/(1+exp(-z))  # pass through an inv-logit function
y = rbinom(n,1,pr)  # response variable
# Build data frame
LogisticStudy1= data.frame(Hipster=y,Transport=x, Irony=j)

ggplot(LogisticStudy1, aes(x=Transport, y=Hipster)) + geom_point() + 
  stat_smooth(method="lm", formula=y~x, se=FALSE)+
  theme_classic()
ggplot(LogisticStudy1, aes(x=Irony, y=Hipster)) + geom_point() + 
  stat_smooth(method="lm", formula=y~x, se=FALSE)+
  theme_classic()

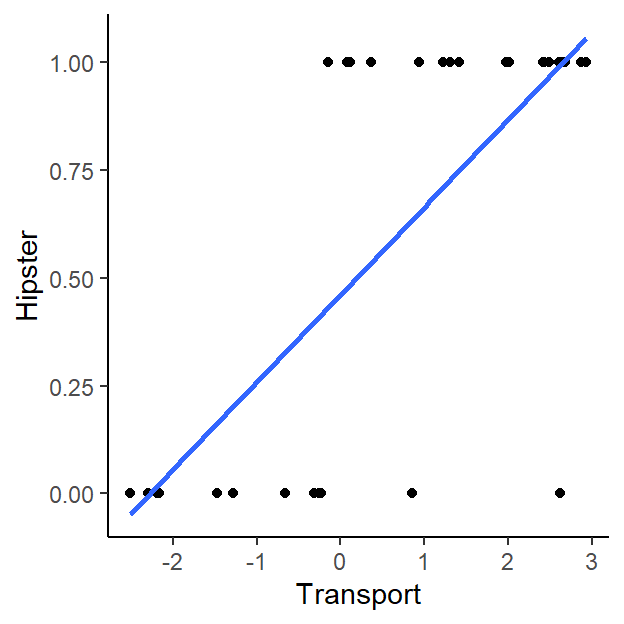
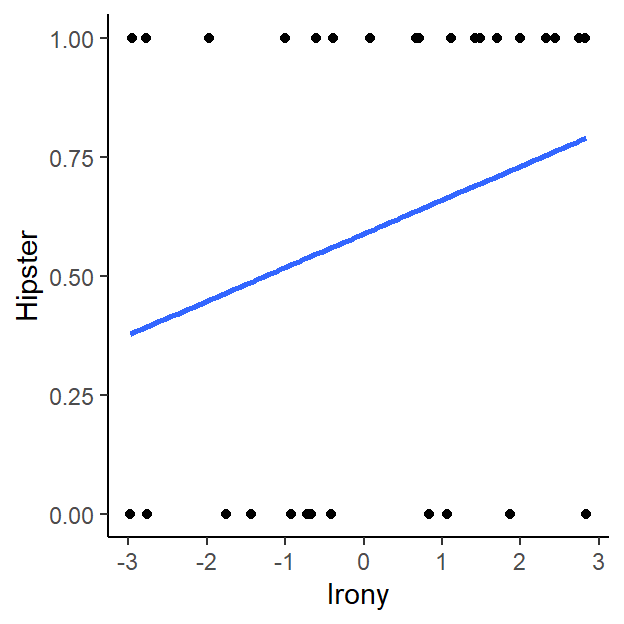- Note in the graphs, all your DVs are at the top and bottom of the graph. - What does that best fit line mean?

• Let’s run our muliple regression: Hipster~ Transport + Irony

LM.1<-lm(Hipster~Transport+Irony,data=LogisticStudy1)

• Using sjPlot (which is like effects package merged into ggplot) we can plot the results

library(sjPlot)
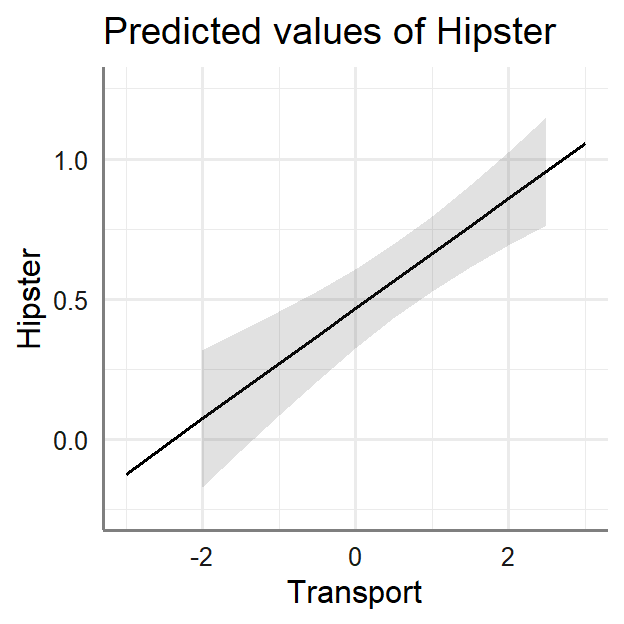
plot_model(LM.1, type = "eff", axis.lim=c(-.25,1.25),
           terms=c("Transport"))+theme_sjplot2()
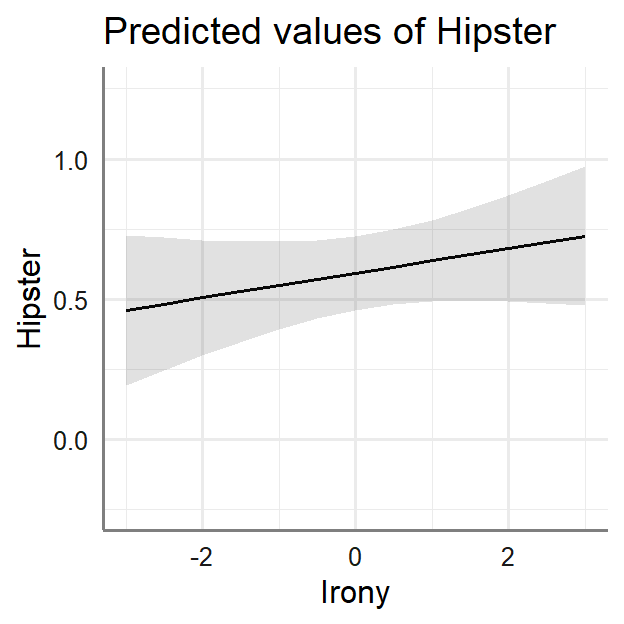
plot_model(LM.1, type = "eff",axis.lim=c(-.25,1.25),
           terms=c("Irony"))+theme_sjplot2()

	Dependent variable:
	Hipster
	LM
Constant	0.459*** (0.069)
Transport	0.196*** (0.038)
Irony	0.044 (0.036)
Observations	30
R2	0.536
Adjusted R2	0.501
F Statistic	15.579*** (df = 2; 27)
Note:	p<0.05; p<0.01; p<0.001

• The intercept reflects the mean Hipster at the mean of the IVs
• The slope of Transport says as weirder their Transport gets the more likely the person is a hipster
• The slope of Irony says as the person uses more irony the more likely the person is a hipster (but it’s not significant)
• How do the residuals look?

plot_model(LM.1, type = "diag")[4]

## [[1]]

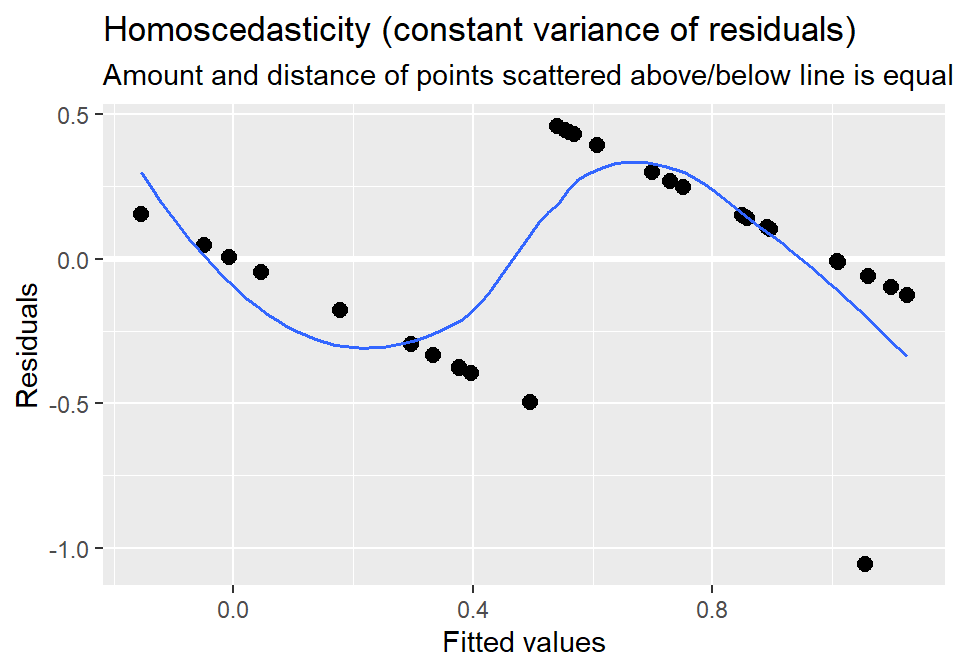
• That looks really odd because the fitted (predict values) are continuous, but the response is binomial
• Let’s see how well we predicted (fit) our result for each individual:
  • Remember to make a “prediction” we solve the regression equations for each subjects IVs the DV (Hipster)

LogisticStudy1$Predicted.Value<-predict(LM.1)
summary(LogisticStudy1$Predicted.Value)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -0.1545  0.3766  0.5883  0.6000  0.8825  1.1243

• Yikes! The model predicted a value outside the range of possible values (value above 1)
• Let’s say any prediction > .5 = Hipster and below that is Not Hipster
• Then we will examine a contingency table (predict results to true results)

LogisticStudy1$Predicted.Hipster<-ifelse(LogisticStudy1$Predicted.Value > .5,1,0)
C.Table<-with(LogisticStudy1,
   table(Predicted.Hipster, Hipster))
C.Table

##                  Hipster
## Predicted.Hipster  0  1
##                 0 11  0
##                 1  1 18

• Correct predict is [0 & 0] and [1 & 1], bad prediction are mismatches
• To get an accurancy score: [11 + 18 ]/ 30 X 100

PercentPredicted<-(C.Table[1,1]+C.Table[2,2])/sum(C.Table)*100

• Yields Accuracy = 96.6666667%

• So the model did a good job making the prediction in this simple case, but the \(R^2\) has no meaning (what variability of Hipster is it explaining?)

Summary

Using linear regression on this data produced odd predictions outside of the bounded range, violation of homoscedasticity, and an \(R^2\) which makes no sense. Instead, let’s try a GLM, but first let’s understand the binomial distribution and logit link function.

Logistic Regression

• Logistic regression is that we call the regression where we analyze binomial DV

Binomial Distribution

• Binomial can be expressed as follows: \[p(n|N) = (\frac{N}{n})p^n(1-p^{N-n})\]
• where \(n\) = successes in \(N\) trials, at a specific \(p\) probability
• These change as function of the underlying probability of getting a 0 or 1
• The plot below has \(N=10\) people making 1 response each, with probability changing from 0 to 1 by .25

par(mfrow=c(1, 5))
for(p in seq(0, 1, len=5))
{
    x <- dbinom(0:10, size=10, p=p)
    barplot(x, names.arg=0:10, space=0)
}

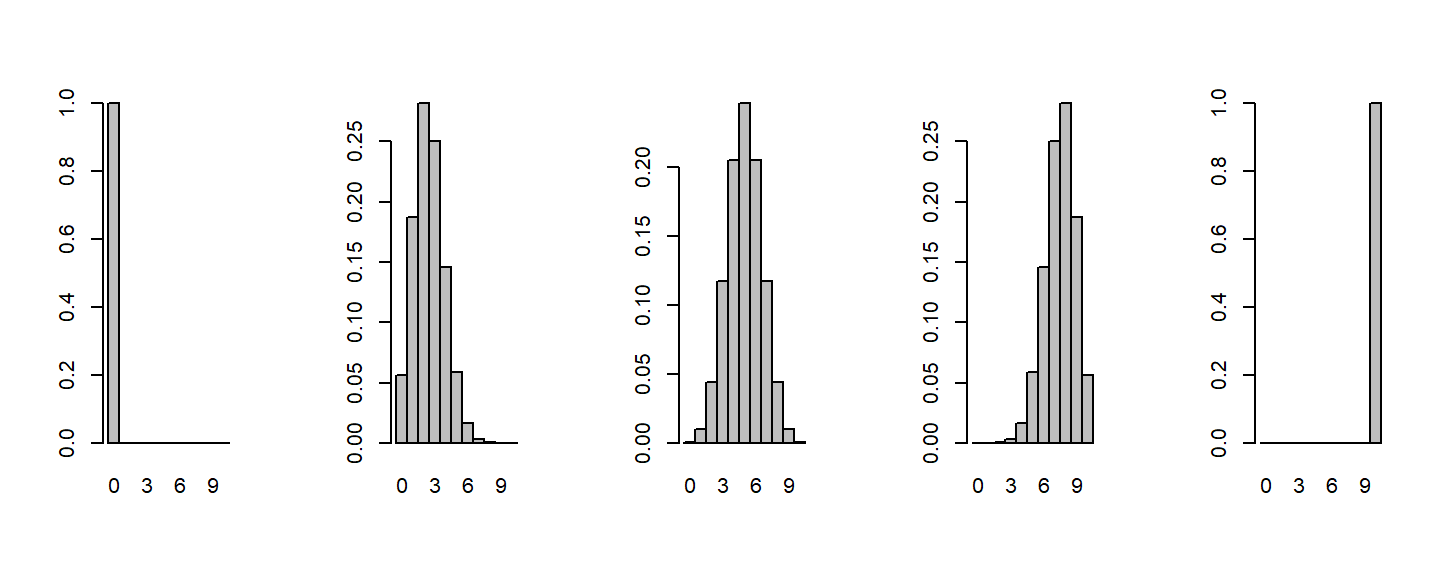
• As the number of people increases, you will notice it looks normal, here is 100 responses

par(mfrow=c(1, 5))
for(p in seq(0, 1, len=5))
{
    x <- dbinom(0:100, size=100, p=p)
    barplot(x, names.arg=0:100, space=0)
}

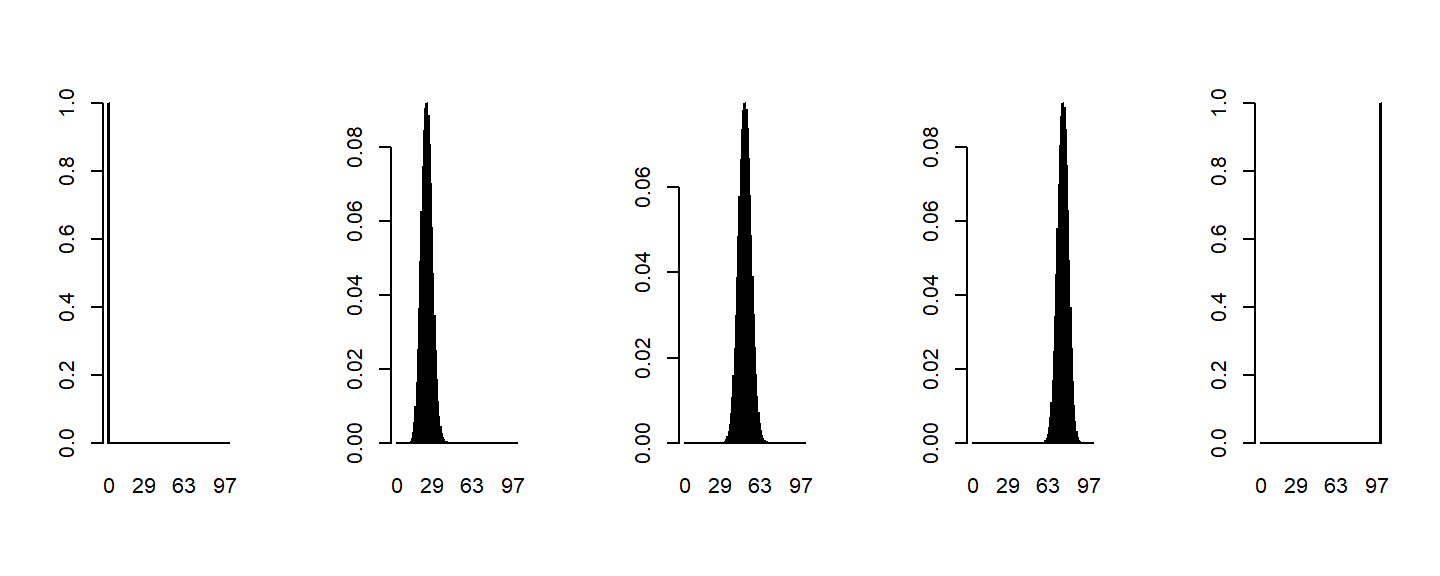
Logit Linking Function

• We can bound our results making our best fit line asymptotic to the boundary conditions
  • To make this work, we need to switch from straight lines to the sigmoid
• Remember regression wants the DV to be between \(-\infty,\infty\), so have will have to apply a the logit transform

\[Logit = log\frac{p}{1-p}\]

• Note: I will use Log for the Natural Log to be consistent with R (but in other places, you might see natural log as LN)

logit.Transform<-function(p) {log(p/(1-p)) }

plot(logit.Transform(seq(0,1,.0001)),seq(0,1,.0001),
     main="Logit Transform",ylim = c(0,1),
  xlab="Logit",ylab="Probability")

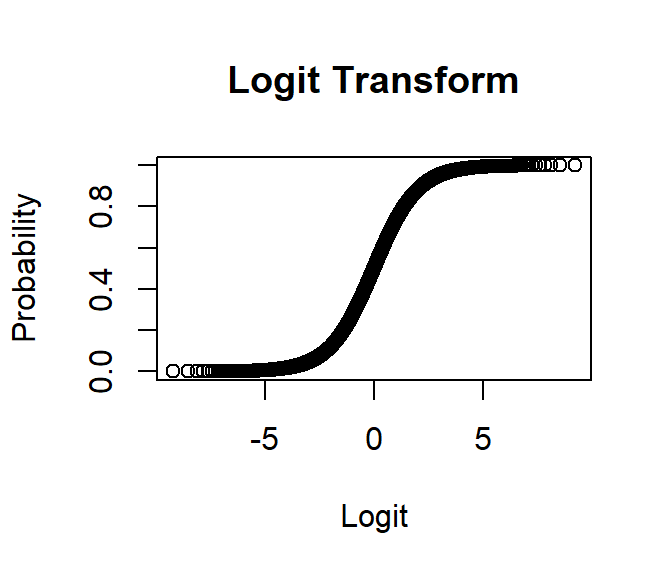
• You can see the sigmoid is asymptotic to the boundary conditions of 0 and 1 probability!

Fit the logistic regression

• \(logit(Hipster) = B_1(Transport) +B_2(Irony) + B_0\)
• This can be accomplished by changing the function in R to glm from lm and specifying the family as binomial(link = “logit”)
• First let’s plot and then make sense of the parameters afterwards

LR.1<-glm(Hipster~Transport+Irony,data=LogisticStudy1, family=binomial(link = "logit"))

Plot in probabilities

• Y-axis = Predicted probability of Hipster as a function of Transport weirdness or Use of Irony
• Using sjPlot (which is like effects package merged into ggplot) we can now see

library(sjPlot)
plot_model(LR.1, type = "eff",
           terms=c("Transport"))+theme_sjplot2()
plot_model(LR.1, type = "eff",
           terms=c("Irony"))+theme_sjplot2()

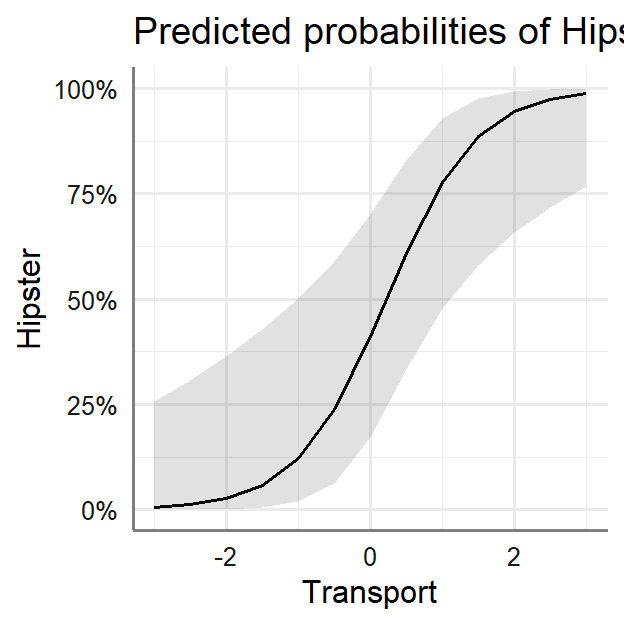
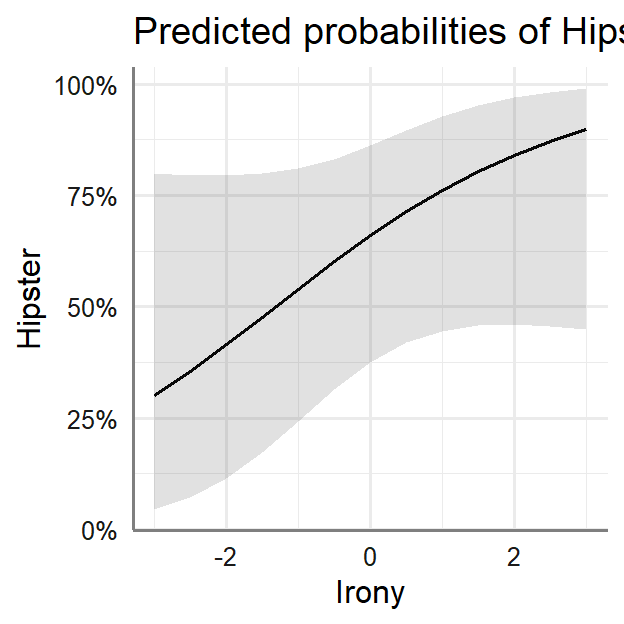
Interpret coefficients

• Raw coefficients are transformed and this hard to makes sense of
• So we can transform them back to something meaningful; odd ratios or probabilities
• Odds ratio = success is defined as the ratio of the probability of success over the probability of failure
• 50% chance = odds ratio of 1 (1:1 ratio)

	Dependent variable:
	Hipster
	Logistic
Constant	-0.441 (0.629)
Transport	1.610** (0.600)
Irony	0.502 (0.338)
Observations	30
Log Likelihood	-9.654
Akaike Inf. Crit.	25.308
Note:	p<0.05; p<0.01; p<0.001

\[Odds = e^{logit(x)}\]

L.to.O.Transform<-function(p) {exp(logit.Transform(p))}

plot((logit.Transform(seq(0,.99,.01))),L.to.O.Transform(seq(0,.99,.01)),
     main="Logit to Odds Transform",
  xlab="Logit",ylab="Odds")

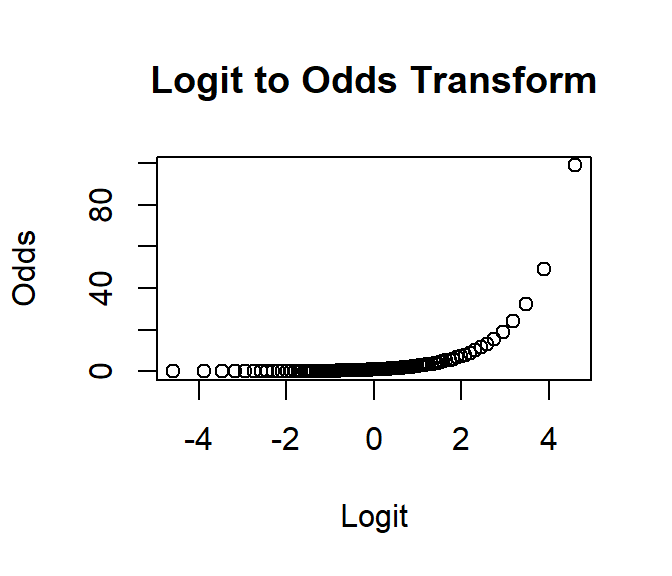- here are our regression estimates as odds ratio

LR.1.Trans <- coef(summary(LR.1))
LR.1.Trans[, "Estimate"] <- exp(coef(LR.1))

	Estimate	Std. Error	z value	Pr(>|z|)
(Intercept)	0.6435201	0.6288280	-0.7009898	0.4833094
Transport	5.0014129	0.5995236	2.6849992	0.0072530
Irony	1.6524682	0.3375908	1.4878075	0.1368017

or you can use the sjplot package

# tab_model(LR.1, 
#          show.se = TRUE,show.aic = TRUE, show.loglik=TRUE,show.ci = FALSE)

• MDs talk in odds, but psychologists sometime prefer probabilities \[P = \frac{Odds} {1 + Odds}\]

O.to.P.Transform<-function(p) {L.to.O.Transform(p)/(1+L.to.O.Transform(p))}

plot(L.to.O.Transform(seq(0,.94,.01)),O.to.P.Transform(seq(0,.94,.01)),
     main="Odds to Probablity Transform",
  xlab="Odds",ylab="Probablity")

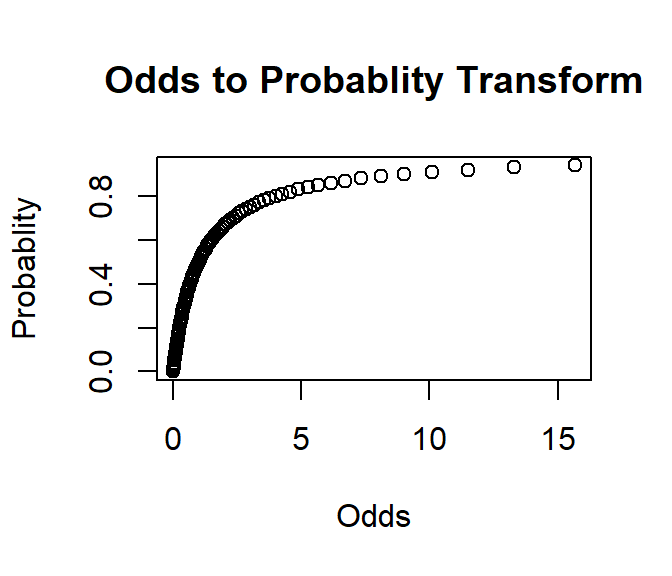
• So we can convert our regression equation to give our probabilities directly

\[p_{(Hipster)} =\frac{e^{(B_1(Transport)+B_2(Irony) + B_0})}{1+e^{(B_1(Transport)+B_2(Irony) + B_0})}\]

• or more simply!

\[p_{(Hipster)} =\frac{1}{1+e^{-(B_1(Transport)+B_2(Irony) + B_0})}\]

LR.1.TransP <- coef(summary(LR.1))
LR.1.TransP[, "Estimate"] <- exp(coef(LR.1))/(1+exp(coef(LR.1)))

	Estimate	Std. Error	z value	Pr(>|z|)
(Intercept)	0.3915499	0.6288280	-0.7009898	0.4833094
Transport	0.8333726	0.5995236	2.6849992	0.0072530
Irony	0.6229927	0.3375908	1.4878075	0.1368017

Note: These probabilities are like the odds ratio. They represent how much more likely the results between the levels of the predictors. They do not tell you the likelihood of being a hipster. For that you must solve the equitation as I showed above. Also you can use effects or sjplot package to plot the results in predicted probabilities.

What to report

• However, you have to report the raw values that come from the logistic regression [or report them in Odds ratios]
• This is because your units are raw (centered) units and if you used this table you would need to figure out how to convert all your IV units
  • Thus, you would simply use the equations above when you add up your predictors
  • So just like in linear regression you would add your predictor estimates (let’s say if you have nominal variables and interactions) and then convert them as above

Wait!! What about my R-squared?

• \(R^2\) has no meaning has no meaning in these models
  • They do not measure the amount of variance accounted for
• Binominal data cannot be homoscedastic, in fact, you could see there is no spread of data around the line, and also the variance at each value may not be same
• Over the years people have created different types of pseudo-\(R^2\) in which to try to make linear regression types of understanding
  • Common favorites are Cox & Snell (aka Maximum likelihood), Nagelkerke (aka Cragg and Uhler’s), McFadden, Efron’s, etc
  • You can see an easy description of each type here: http://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-pseudo-r-squareds/
• Each of them tries to capture something like our original \(R^2\), such as (A) explaining variability, (B) model improvement such as \(change in R^2\) between models, (C) and finally as a measure of multiple-correlation
• Many of these between testing between a restricted model (Null model) and your model, so first we need to examine model fitting for GLMs

Deviance Testing

• In linear regression, OLS was the fitting procedure, and it worked because OLS can find mean and variance of the normal distribution, but now we are not working with normal distributions, so we need a new fitting procedure
  • In our OLS regression we had this concept: \[SS_{Resid} = SS_Y - SS_{Regression}\]
    • In other words, residual = Actual - Fitted values
  • in OLS, we can get the best fit analytically (solving an equation), but with GLM you cannot do that!
• For GLM, We can calculate the deviance of scores, which is built on the idea of maximum likelihood
  • We iterate a solution (since we cannot solve it without trial and error)
  • We need to find the likelihood; which is “a hypothetical probability that an event that has already occurred would yield a specific outcome” (http://mathworld.wolfram.com/Likelihood.html)
  • We will iterate through parameters until we maximize our likelihood (called maximal likelihood estimation)
  • There are different ML (or just L) functions that can be used and they can apply to most distributions
  • When the fit is perfect, \[L_{perfect} = 1\]
  • The null case (starting model) that ONLY has an intercept, this will probably yield the lowest likelihood
    • Our test model will be intercept + predictors (parameters - k)

\[Likelihood ratio =\frac{L_{Simple}}{L_{Complex}}\]

• Deviance this is the \(-2*\) natural logLikelihood ratio \[D = 2*log(Likelihood ratio)\] AKA \[D = -2LL\] First, I will show you the pseudo-\(R^2\) and then we will examine how to test between model fits

• Null Deviance \[D_{Null} = -2[log(L_{Null}) - log(L_{Perfect})]\]

• Model Deviance \[D_{K} = -2[log(L_{K} - log(L_{Perfect})]\]

• This is like our SS residual from OLS

Pseudo-R-sqaured

• We need those crazy Devience scores for some of our pseudo-\(R^2\) measurements, for example: \[R_L^2 = \frac{D_{Null} -D_{k}}{D_{Null}}\]
• Cox and Snell is what SPSS gives and people report it often
  • Nagelkerke is an improvement (C&S) as it corrects some problems
• But people like McFadden’s cause its easy to understand

\[R_{McFadden}^2 = 1 - \frac{LL_{k}}{LL_{Null}}\]

• We can just get them from the pscl package
• llh = log-likelihood from the fitted model (llk above)
• llhNull = The log-likelihood from the intercept-only restricted model
• \(G^2 = -2(LL_{K} - LL_{NULL})\) is a one of the proposed goodness of fit measures (we will come back to this later)
• McFadden = McFadden pseudo-\(R^2\)
• r2ML = Cox & Snell pseudo-\(R^2\)
• r2CU = Nagelkerke pseudo-\(R^2\)

library(pscl)
pR2(LR.1)

## fitting null model for pseudo-r2
##         llh     llhNull          G2    McFadden        r2ML        r2CU 
##  -9.6542125 -20.1903500  21.0722750   0.5218403   0.5046096   0.6821567

Wait why I do see Z and not t-values?

• When testing individual predictors, you do not see t-tests you are looking at Wald Z-scores
• Some argue that individual predictors should tested against a model that does not have that term (like a stepwise regression), but our programs will calculate a test-statistics based on each predictor in the model (more people ignore these and just look at the change in overall model fit)

\[ Wald = \frac{B_j}{SE_{B_j}^2}\]

• Wald z-scores follow a chi-square distribution

• Or you can run a stepwise and test each predictor again the null model like this (order of predictors matter)

anova(LR.1, test="Chisq")

## Analysis of Deviance Table
## 
## Model: binomial, link: logit
## 
## Response: Hipster
## 
## Terms added sequentially (first to last)
## 
## 
##           Df Deviance Resid. Df Resid. Dev Pr(>Chi)    
## NULL                         29     40.381             
## Transport  1  18.5679        28     21.813 1.64e-05 ***
## Irony      1   2.5044        27     19.308   0.1135    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Hierarchical testing

• Going stepwise can be difficult if you have lots of predictors
• Since we cannot test the change in \(R^2\) we will instead test whether the deviance is significantly greater than the model without the predictor (just like above)
• So we run likelihood ratio test between the models which tests against the chi-square distribution

LR.Model.1<-glm(Hipster~Irony,data=LogisticStudy1, family=binomial(link = "logit"))
LR.Model.2<-glm(Hipster~Irony+Transport,data=LogisticStudy1, family=binomial(link = "logit"))
anova(LR.Model.1,LR.Model.2,test = "Chisq")

## Analysis of Deviance Table
## 
## Model 1: Hipster ~ Irony
## Model 2: Hipster ~ Irony + Transport
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1        28     38.294                          
## 2        27     19.308  1   18.986 1.317e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Here we see model 2 has improvement in deviance (it fits better) and thus it means Transport did help the prediction

How well am I predicting?

• Model 1

fitted.results <- predict(LR.Model.1,newdata=LogisticStudy1,type='response')
fitted.results <- ifelse(fitted.results > 0.5,1,0)
misClasificError <- mean(fitted.results != LogisticStudy1$Hipster)
print(paste('Accuracy = ',round(1-misClasificError,3)))

## [1] "Accuracy =  0.633"

• Model 2

fitted.results <- predict(LR.Model.2,newdata=LogisticStudy1,type='response')
fitted.results <- ifelse(fitted.results > 0.5,1,0)
misClasificError <- mean(fitted.results != LogisticStudy1$Hipster)
print(paste('Accuracy = ',round(1-misClasificError,3)))

## [1] "Accuracy =  0.967"

• This is not the only way to examine accuracy
  • To get correct responses, misses and false alarms (remember our type I and II boxes)
  • To visualize this, we will examine receiver operator curves (ROC)
    • It is the relationship between correct responses and false alarms

library(ROCR)
fitted.results <- predict(LR.Model.2,newdata=LogisticStudy1,type='response')
pr <- prediction(fitted.results, LogisticStudy1$Hipster)

prf <- performance(pr, measure = "tpr", x.measure = "fpr")
plot(prf)

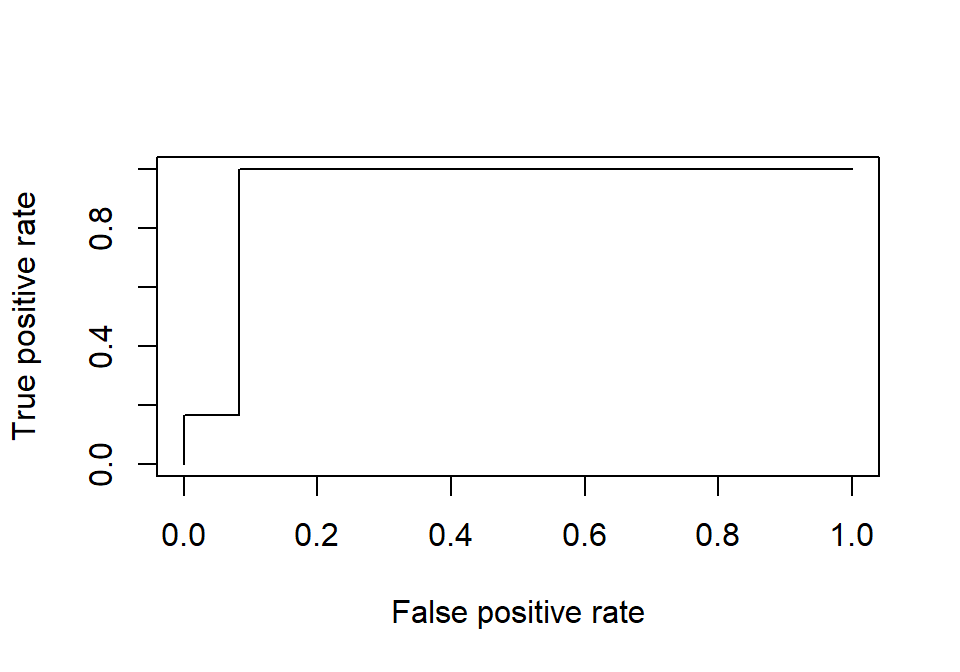
• We will calculate the area under the curve to get a good measure of accuracy (the closer to 1 the better)
  • Also, the curve should follow the shape you see below (if it is the opposite shape you have a problem)

auc <- performance(pr, measure = "auc")
auc <- auc@y.values[[1]]
print(paste('Area under the Curve = ',round(auc,3)))

## [1] "Area under the Curve =  0.931"

Interactions

• Just like in multiple regression you test for interactions

LR.Model.2<-glm(Hipster~Transport+Irony,data=LogisticStudy1, family=binomial(link = "logit"))
LR.Model.3<-glm(Hipster~Transport*Irony,data=LogisticStudy1, family=binomial(link = "logit"))
anova(LR.Model.2,LR.Model.3,test = "Chisq")

## Analysis of Deviance Table
## 
## Model 1: Hipster ~ Transport + Irony
## Model 2: Hipster ~ Transport * Irony
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)  
## 1        27     19.308                       
## 2        26     16.410  1   2.8979  0.08869 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• There is no improvement of fit, but here are the models side by side

	Dependent variable:
	Hipster
	Main Effects	Interaction
	(1)	(2)
Constant	-0.441 (0.629)	-1.272 (1.047)
Transport	1.610** (0.600)	2.238* (0.964)
Irony	0.502 (0.338)	0.925 (0.499)
Transport:Irony		-0.613 (0.433)
Observations	30	30
Log Likelihood	-9.654	-8.205
Akaike Inf. Crit.	25.308	24.410
Note:	p<0.05; p<0.01; p<0.001

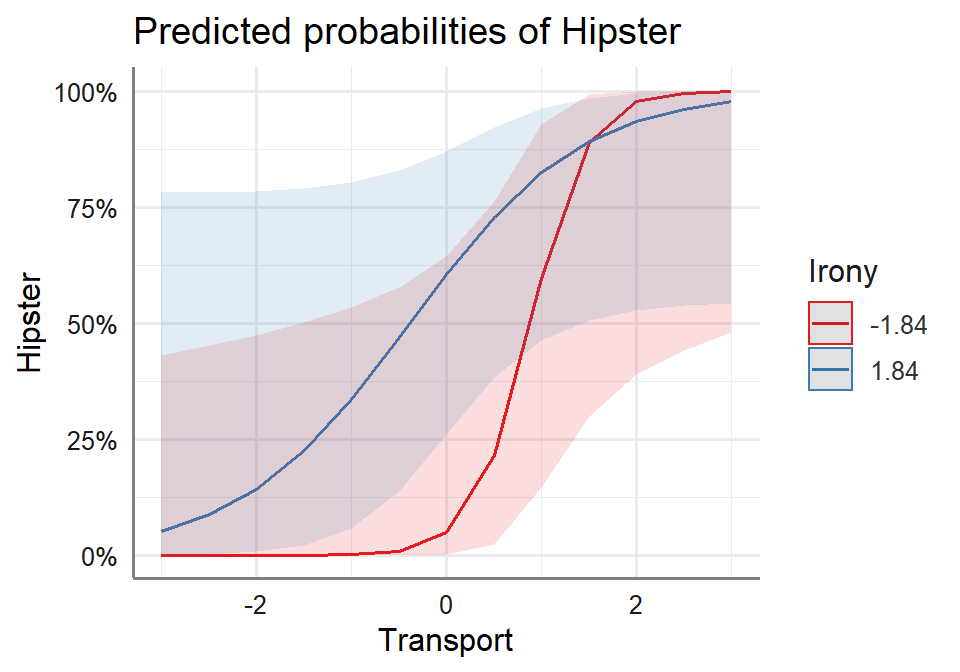
• We can plot them (even though they are not significant).

• We can use sjPlot you must manually set the level for which you want to see the moderator (like we did with Rockchalk). You can set SD and for Irony that values is 1.84 or whatever moderator values you want. Note you cannot pass the variables, you must hand type them.

plot_model(LR.Model.3, type = "pred", 
           terms = c("Transport", "Irony [-1.84,1.84]"))+
  theme_sjplot2()

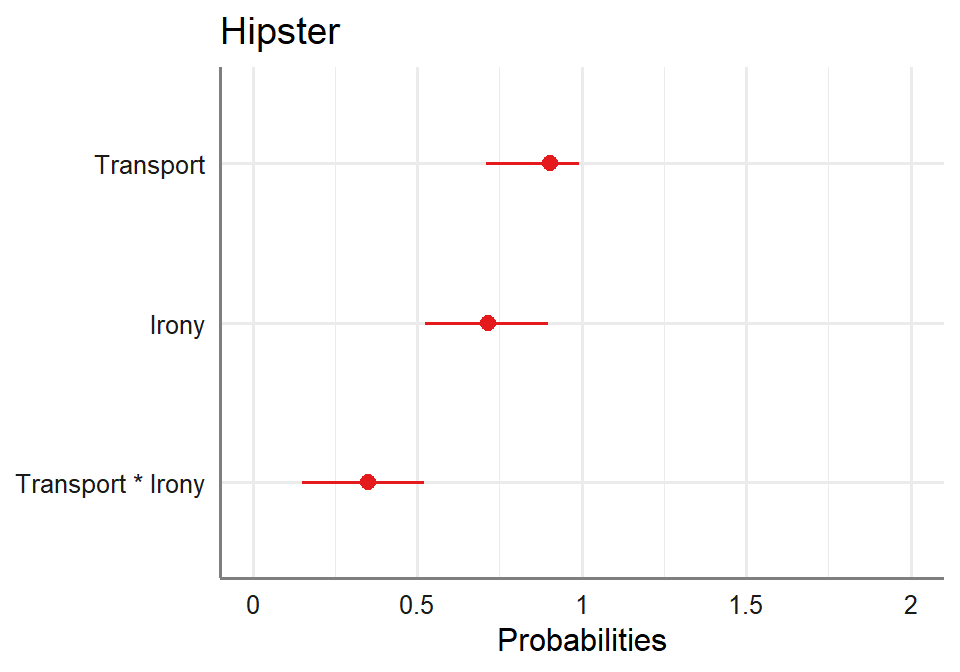
Other types of plots

• You can also plot forest plots. This is useful when you have lots of predicts
• You will want these values to not overlap .50 (an odds of 1:1) or coin flip

plot_model(LR.Model.3, transform = "plogis")+theme_sjplot2()

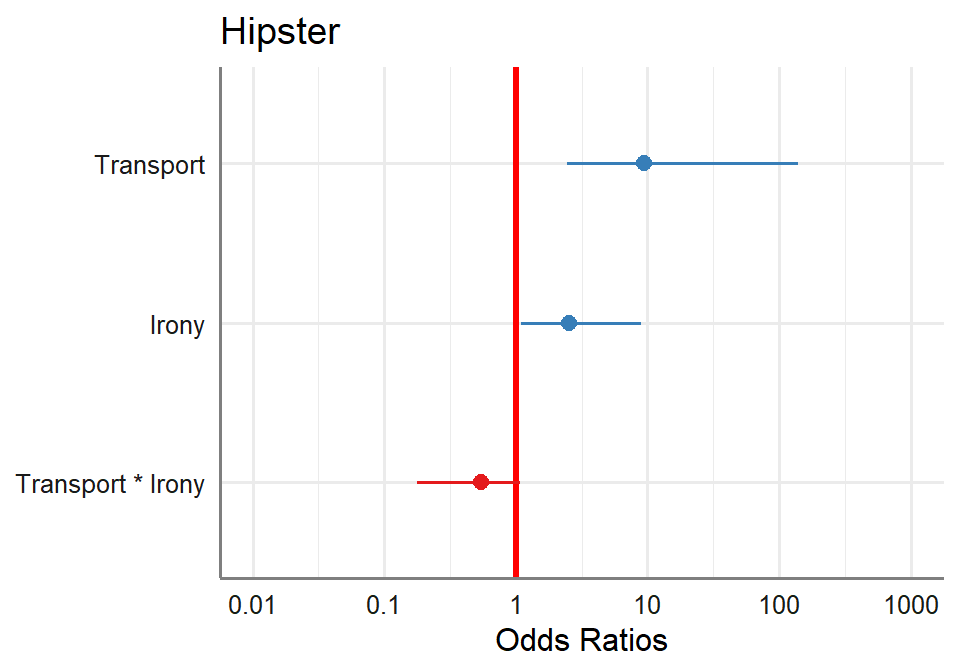
• see them in odd ratios below

plot_model(LR.Model.3, vline.color = "red")+theme_sjplot2()